关于卡尔曼滤波的原理

关于卡尔曼滤波的原理

1.基本模型的建立

我们假设我们的系统的状态量有这样的线性的递归关系：
$$x_k=F_k{x}_{k-1}+B_k{u}_k$$

为了辅助读者理解，我们以匀速直线运动为例子，我们以位置(p)和速度(v)为状态量，状态检测的周期为Δt：

$$x_k=\left[\begin{array}{c}{p}_k\\ v_k\end{array}\right]=\left[\begin{array}{cc}1& \Delta t\\ 0& 1\end{array}\right]\left[\begin{array}{c}{p}_{k-1}\\ v_{k-1}\end{array}\right]=F_k{x}_{k-1}$$

在这里，F_k则表示前一个状态量和当前状态量的递归关系。

我们再引用变速直线运动的例子来解释B_k和u_k:

$$x_k=\left[\begin{array}{c}{p}_k\\ v_k\end{array}\right]=\left[\begin{array}{cc}1& \Delta t\\ 0& 1\end{array}\right]\left[\begin{array}{c}{p}_{k-1}\\ v_{k-1}\end{array}\right]+\left[\begin{array}{c}\frac{1}{2}\Delta t^2\\ \Delta t\end{array}\right]a=F_k{x}_{k-1}+B_k{u}_k$$

匀速直线运动是物体在不受到合力的作用的时候所做的运动，其状态改变与外界无关，所以其状态只与上一检测时刻的状态相关。而变速直线运动，其运动状态的改变与加速度相关，加速度和合外力作用挂钩，所以在这个情景下，状态的变化不仅与上一观察时刻的状态相关，与当前的外界输入也相关。

为了描述一维观察量的精确程度，我们用方差这个统计量来表征。对于多维的随机变量，我们则用协相关矩阵来表征：
$$P_k=E(x_k{x}_k^T)=\left[\begin{array}{cc}{\Sigma }_{pp}& {\Sigma }_{pv}\\ {\Sigma }_{vp}& {\Sigma }_{vv}\end{array}\right]$$

对于状态变量x的协相关矩阵，根据其性质，我们可以得到其递归表达式：

$$P_k=F_k{P}_{k-1}{F}_k^T$$

2.引入干扰的情况

但是实际上，我们的状态观察往往存在各种各样的干扰，我们由中心极限定理，可以认为在大多数情境下，干扰服从高斯分布。我们的递归表达式也变为：
$$\begin{gathered} x_k=F_k{x}_{k-1}+B_k{u}_k+w_k \\ {w}_k\sim N(0,Q_k) \end{gathered}$$

于是我们的协相关矩阵的实际的递归表达式也应该为：

$$P_k=F_k{P}_{k-1}{F}_k^T+Q_k$$
不难看出，如果我们一直使用递归的形式来求下一观察时刻的状态观察值，那么最后协相关矩阵也可能会越来越大而不收敛。这也是为什么我们一般不会单独采用会累计误差的测量方法比如积分法的原因。

这个时候，数据融合的优势就体现出来了，加入我们还有一组传感器，它们可以测量出与x相关的被测量，我们假设传感器的测量值组成的矩阵为y,令传感器所测物理量和被观察状态物理量满足线性关系，用矩阵可以表示为：

$$y=Hx$$
我们可以认为传感器的测量值Y和递归估计值Hx这两个随机变量都分别服从两个高斯分布：

$$\begin{gathered} H_k{x}_k\sim N(H_k{\hat{x}}_k,H_k{P}_k{H}_k^T) \\ Y\sim N(y_k,R) \end{gathered}$$

3.减少干扰的思路

（图源：百家号-CSDN学院）

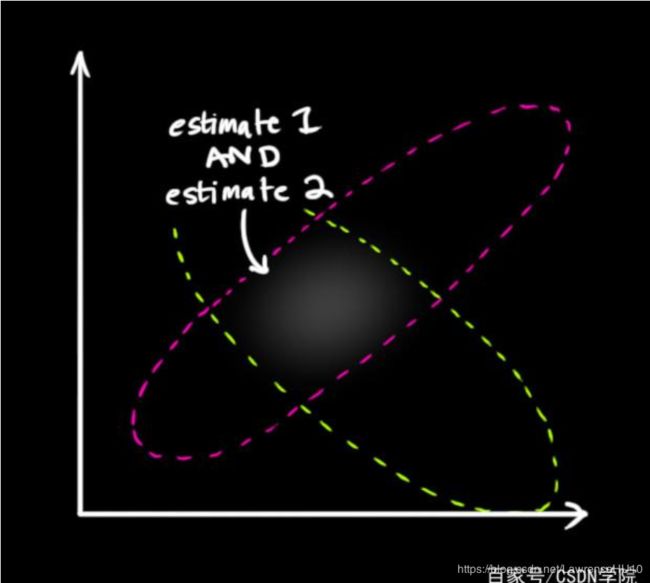
我们由上一部分的分析可以得知，当我们传感器测量值Y和状态改变的估计值Hx都服从两个正态分布，假设我们的观测量和测量量都是二维的，那么如图所示，这两个正态分布分布在绿色和红色两个区域（++注意：事实上服从正态分布的随机变量是不会有界的，但是我们一般认为其范围在μ±3σ之内，多维正态分布随机变量也同理++）。如果我们将这两个随机变量的概率密度函数相乘，再将其归一化，不就可以得到一个方差更小的分布吗？

对于一个服从n维正态分布的随机变量，其概率密度函数为：

$$\begin{gathered} p(x;{\mu }_1,{\Sigma }_1)=\frac{1}{(2\pi {)}^{\frac{n}{2}}|{\Sigma }_1{|}^{\frac{1}{2}}}\exp (-\frac{1}{2}(x-{\mu }_1{)}^T{\Sigma }_1^{-1}(x-{\mu }_1)) \\ p(x;{\mu }_2,{\Sigma }_2)=\frac{1}{(2\pi {)}^{\frac{n}{2}}|{\Sigma }_2{|}^{\frac{1}{2}}}\exp (-\frac{1}{2}(x-{\mu }_2{)}^T{\Sigma }_2^{-1}(x-{\mu }_2)) \end{gathered}$$

两个概率密度函数做乘法再重新做归一化之后，所得的概率密度函数是一个高斯分布的概率密度函数，其均值和方差分别满足：
$$\begin{gathered} {\mu }^{\prime }={\mu }_1+K({\mu }_2-{\mu }_1) \\ {\Sigma }^{\prime }={\Sigma }_1-K{\Sigma }_1 \end{gathered}$$
其中：

$$K={\Sigma }_1({\Sigma }_1+{\Sigma }_2{)}^{-1}$$

这样，我们就可以从概率分布与统计的角度减少了干扰对我们测量值的影响。

值得注意的是，我们的两个高斯分布真的会像这一部分刚开始所展示的图中所示的那样吗？答案肯定是否。但是我们在设定方案时，要尽量使我们的两个正态分布满足这样的关系。比如我们用于姿态结算的9轴传感器，就是利用陀螺仪来得到角速度，再利用角速度递归运算得到欧拉角，再利用加速度计和磁力计这两个可以获取绝对欧拉角的传感器来对结果做修正。这个数据融合的方式就可以选择卡尔曼滤波。陀螺仪可以得到较为准确的角速度信息，但是用其求欧拉角难免会存在累计误差，而加速度传感器和磁力计则没有累计误差，但是在运动时误差会很大，这三种传感器的测量结果恰好和图中的特性一致，利用卡尔曼滤波的方式则可以实现优势互补。

4.卡尔曼滤波的递归公式

根据第三部分所讲，我们可以用概率密度函数相乘的方式得到一个新的高斯分布，我们可以用这个新的高斯分布的均值和方差，作为我们新的状态值和其协相关矩阵的最优估计。

首先我们可以得到传感器测量值y的最佳估计：
$$\begin{gathered} Y_k^{\prime }=H_k{\hat{x}}_k+K^{\prime }(y_k-H_k{\hat{x}}_k) \\ {\Sigma }_{Y_k}=H_k{P}_k{H}_k^T-K^{\prime }{H}_k{P}_k{H}_k^T \end{gathered}$$
其中：
$$K^{\prime }=H_k{P}_k{H}_k^T(H_k{P}_k{H}_k^T+R{)}^{-1}$$
我们再根据物理量y与x的关系，得到x关于y的函数：
$$x=H^{-1}y$$
于是我们对观察状态x的最优估计就可以写为：
$$\begin{gathered} {\hat{X}}_k^{\prime }=H_k^{-1}{Y}_k^{\prime }={\hat{x}}_k+K(y_k-H_k{\hat{x}}_k) \\ {P}_k^{\prime }=P_k-K{H}_k{P}_k \\ K=H_k^{-1}{K}^{\prime }=P_k{H}_k^T(H_k{P}_k{H}_k^T+R{)}^{-1} \end{gathered}$$

那么综上所述，卡尔曼滤波关于观测状态x的递归公式为：
$$\begin{gathered} {\hat{x}}_k=F_k{\hat{x}}_{k-1}+B_k{u}_k \\ {\hat{P}}_k=F_k{P}_{k-1}{F}_k^T+Q \\ {\hat{X}}_k^{\prime }={\hat{x}}_k+K(y_k-H_k{\hat{x}}_k) \\ {P}_k^{\prime }=(I-K{H}_k)P_k \\ K=P_k{H}_k^T(H_k{P}_k{H}_k^T+R{)}^{-1} \end{gathered}$$
值得注意的是，应用卡尔曼滤波的时候，我们必须要了解测量误差的方差R和过程误差的方差Q。 对于经典的卡尔曼滤波器，这两个值则需要我们通过测量和估计得到，之后有机会再深入研究一下。

5.参考资料

1.详解卡尔曼滤波原理——CSDN学院

2.【图灵鸡】什么是卡尔曼滤波？其实一点也不难！详解卡尔曼滤波