凉肝的题解
凉肝的题解
- A. Mezo Playing Zoma
- Input
- Output
- Example
- Note
- 题解
- B. Just Eat It!
- Input
- Output
- Example
- Note
- 题解
- C. Fadi and LCM
- Input
- Output
- Examples
- 题解
- D. Dr. Evil Underscores
- Input
- Output
- Examples
- Note
- 题解
- E. Deadline
- Input
- Output
- Example
- Note
- 题解
- F. Yet Another Meme Problem
- Input
- Output
- Example
- 题解
- G. HQ9+
- Input
- Output
- Examples
- Note
- 题解
- H. Rolling The Polygon
- Input
- Output
- Example
- 题解
A. Mezo Playing Zoma
Today, Mezo is playing a game. Zoma, a character in that game, is initially at position x=0. Mezo starts sending n commands to Zoma. There are two possible commands:
- ‘L’ (Left) sets the position x:=x−1;
- ‘R’ (Right) sets the position x:=x+1.
Unfortunately, Mezo’s controller malfunctions sometimes. Some commands are sent successfully and some are ignored. If the command is ignored then the position x doesn’t change and Mezo simply proceeds to the next command.
For example, if Mezo sends commands “LRLR”, then here are some possible outcomes (underlined commands are sent successfully):
- “LRLR” — Zoma moves to the left, to the right, to the left again and to the right for the final time, ending up at position 0;
- “LRLR” — Zoma recieves no commands, doesn’t move at all and ends up at position 0 as well;
- “LRLR” — Zoma moves to the left, then to the left again and ends up in position −2.
Mezo doesn’t know which commands will be sent successfully beforehand. Thus, he wants to know how many different positions may Zoma end up at.
Input
The first line contains n (1≤n≤ 1 0 5 10^5 105) — the number of commands Mezo sends.
The second line contains a string s of n commands, each either ‘L’ (Left) or ‘R’ (Right).
Output
Print one integer — the number of different positions Zoma may end up at.
Example
Input
4
LRLR
Output
5
Note
In the example, Zoma may end up anywhere between −2 and 2.
题解
相当于对字串里的字符进行任意的组合,取得的结果可能性范围是所有的 R R R加起来以及所有的 L L L加起来所形成的区间长度.
#pragma comment(linker, "/STACK:102400000,102400000")
#include B. Just Eat It!
Today, Yasser and Adel are at the shop buying cupcakes. There are n cupcake types, arranged from 1 to n on the shelf, and there are infinitely many of each type. The tastiness of a cupcake of type i is an integer ai. There are both tasty and nasty cupcakes, so the tastiness can be positive, zero or negative.
Yasser, of course, wants to try them all, so he will buy exactly one cupcake of each type.
On the other hand, Adel will choose some segment [l,r] ( 1 ≤ l ≤ r ≤ n 1≤l≤r≤n 1≤l≤r≤n) that does not include all of cupcakes (he can’t choose [l,r]=[1,n]) and buy exactly one cupcake of each of types l , l + 1 , … , r . l,l+1,…,r. l,l+1,…,r.
After that they will compare the total tastiness of the cupcakes each of them have bought. Yasser will be happy if the total tastiness of cupcakes he buys is strictly greater than the total tastiness of cupcakes Adel buys regardless of Adel’s choice.
For example, let the tastinesses of the cupcakes be [7,4,−1]. Yasser will buy all of them, the total tastiness will be 7+4−1=10. Adel can choose segments [7],[4],[−1],[7,4] or [4,−1], their total tastinesses are 7,4,−1,11 and 3, respectively. Adel can choose segment with tastiness 11, and as 10 is not strictly greater than 11, Yasser won’t be happy
Find out if Yasser will be happy after visiting the shop.
Input
Each test contains multiple test cases. The first line contains the number of test cases t (1≤t≤104). The description of the test cases follows.
The first line of each test case contains n (2≤n≤105).
The second line of each test case contains n integers a1,a2,…,an (−109≤ a i a_i ai≤109), where ai represents the tastiness of the i t h i_{th} ith type of cupcake.
It is guaranteed that the sum of n over all test cases doesn’t exceed 1 0 5 10^5 105.
Output
For each test case, print “YES”, if the total tastiness of cupcakes Yasser buys will always be strictly greater than the total tastiness of cupcakes Adel buys regardless of Adel’s choice. Otherwise, print “NO”.
Example
Input
3
4
1 2 3 4
3
7 4 -1
3
5 -5 5
Output
YES
NO
NO
Note
In the first example, the total tastiness of any segment Adel can choose is less than the total tastiness of all cupcakes.
In the second example, Adel will choose the segment [1,2] with total tastiness 11, which is not less than the total tastiness of all cupcakes, which is 10.
In the third example, Adel can choose the segment [3,3] with total tastiness of 5. Note that Yasser’s cupcakes’ total tastiness is also 5, so in that case, the total tastiness of Yasser’s cupcakes isn’t strictly greater than the total tastiness of Adel’s cupcakes.
题解
如果,这个序列存在一个非正的前缀和或者后缀和,我们删除它,这样,我们可以选出一个子串使得其和大于总和.
而对于其他的情况,我们可以知道,不存在能够让子串大于总和的情况了.
#pragma comment(linker, "/STACK:102400000,102400000")
#include C. Fadi and LCM
Today, Osama gave Fadi an integer X X X, and Fadi was wondering about the minimum possible value of m a x ( a , b ) max(a,b) max(a,b) such that L C M ( a , b ) LCM(a,b) LCM(a,b) equals X X X. Both a a a and b b b should be positive integers.
L C M ( a , b ) LCM(a,b) LCM(a,b) is the smallest positive integer that is divisible by both a a a and b b b. For example, L C M ( 6 , 8 ) = 24 , L C M ( 4 , 12 ) = 12 , L C M ( 2 , 3 ) = 6 LCM(6,8)=24, LCM(4,12)=12, LCM(2,3)=6 LCM(6,8)=24,LCM(4,12)=12,LCM(2,3)=6.
Of course, Fadi immediately knew the answer. Can you be just like Fadi and find any such pair?
Input
The first and only line contains an integer X ( 1 ≤ X ≤ 1 0 12 X(1≤X≤10^{12} X(1≤X≤1012).
Output
Print two positive integers, a a a and b b b, such that the value of m a x ( a , b ) max(a,b) max(a,b) is minimum possible and L C M ( a , b ) LCM(a,b) LCM(a,b) equals X X X. If there are several possible such pairs, you can print any.
Examples
Input
2
Output
1 2
Input
6
Output
2 3
Input
4
Output
1 4
Input
1
Output
1 1
题解
这个题目,就是给一个最小公倍数 n n n,求两个数 a , b a,b a,b.
还要求求出的两个数的最大值最小.
自然想到在给定数的因子里寻找 a a a.
再判断 b = n a b=\dfrac{n}{a} b=an, a , b a,b a,b的最小公倍数是否为 n n n即可.
#pragma comment(linker, "/STACK:102400000,102400000")
#include D. Dr. Evil Underscores
Today, as a friendship gift, Bakry gave Badawy n n n integers a 1 , a 2 , … , a n a_1,a_2,…,a_n a1,a2,…,an and challenged him to choose an integer X X X such that the value m a x 1 ≤ i ≤ n ( a i ⊕ X ) \underset{1≤i≤n}{max}(a_i⊕X) 1≤i≤nmax(ai⊕X) is minimum possible, where ⊕ ⊕ ⊕ denotes the bitwise X O R XOR XOR operation.
As always, Badawy is too lazy, so you decided to help him and find the minimum possible value of m a x 1 ≤ i ≤ n ( a i ⊕ X ) \underset{1≤i≤n}{max}(a_i⊕X) 1≤i≤nmax(ai⊕X).
Input
The first line contains integer n ( 1 ≤ n ≤ 1 0 5 ) n (1≤n≤10^5) n(1≤n≤105).
The second line contains n integers a 1 , a 2 , … , a n ( 0 ≤ a i ≤ 2 30 − 1 ) a_1,a_2,…,a_n (0≤a_i≤2^{30−1}) a1,a2,…,an(0≤ai≤230−1).
Output
Print one integer — the minimum possible value of m a x 1 ≤ i ≤ n ( a i ⊕ X ) \underset{1≤i≤n}{max}(ai⊕X) 1≤i≤nmax(ai⊕X).
Examples
Input
3
1 2 3
Output
2
Input
2
1 5
Output
4
Note
In the first sample, we can choose X=3.
In the second sample, we can choose X=5.
题解
按位递归.
- 如果该为有 1 1 1也有 0 0 0,我们将其分成两组,分别递归,因为两者都有的话,无论怎么 X O R XOR XOR,所得结果在该位都有 1 1 1,于是 a n s = a n s + 2 k ans=ans+2^{k} ans=ans+2k
- 如果只有 1 1 1或者只有 0 0 0,直接递归,因为可以避免该位 X O R XOR XOR为 1 1 1
依次递归,求得结果
#pragma comment(linker, "/STACK:102400000,102400000")
#include E. Deadline
Adilbek was assigned to a special project. For Adilbek it means that he has n days to run a special program and provide its results. But there is a problem: the program needs to run for d days to calculate the results.
Fortunately, Adilbek can optimize the program. If he spends x x x ( x x x is a non-negative integer) days optimizing the program, he will make the program run in ⌈ d x + 1 ⌉ ⌈\frac{d}{x+1}⌉ ⌈x+1d⌉ days ( ⌈ a ⌉ ⌈a⌉ ⌈a⌉ is the ceiling function: ⌈ 2.4 ⌉ = 3 , ⌈ 2 ⌉ = 2 ⌈2.4⌉=3, ⌈2⌉=2 ⌈2.4⌉=3,⌈2⌉=2). The program cannot be run and optimized simultaneously, so the total number of days he will spend is equal to x + ⌈ d x + 1 ⌉ x+⌈\frac{d}{x+1}⌉ x+⌈x+1d⌉.
Will Adilbek be able to provide the generated results in no more than n n n days?
Input
The first line contains a single integer T ( 1 ≤ T ≤ 50 ) T (1≤T≤50) T(1≤T≤50) — the number of test cases.
The next T T T lines contain test cases – one per line. Each line contains two integers n n n and d ( 1 ≤ n ≤ 1 0 9 , 1 ≤ d ≤ 1 0 9 ) d (1≤n≤10^9, 1≤d≤10^9) d(1≤n≤109,1≤d≤109) — the number of days before the deadline and the number of days the program runs.
Output
Print T answers — one per test case. For each test case print YES (case insensitive) if Adilbek can fit in n days or NO (case insensitive) otherwise.
Example
Input
3
1 1
4 5
5 11
Output
YES
YES
NO
Note
In the first test case, Adilbek decides not to optimize the program at all, since d ≤ n d≤n d≤n.
In the second test case, Adilbek can spend 1 day optimizing the program and it will run ⌈ 5 2 ⌉ ⌈\frac{5}{2}⌉ ⌈25⌉=3 days. In total, he will spend 4 days and will fit in the limit.
In the third test case, it’s impossible to fit in the limit. For example, if Adilbek will optimize the program 2 days, it’ll still work ⌈ 11 2 + 1 ⌉ ⌈\frac{11}{2+1}⌉ ⌈2+111⌉=4 days.
题解
给一个天数 n n n,以及工作需要时间 d d d,以及一个优化时间的方式,将 d d d转变为 x + ⌈ d x + 1 ⌉ x+⌈\frac{d}{x+1}⌉ x+⌈x+1d⌉.
也就是判断 d d d是否小于 n n n,最小的 x + ⌈ d x + 1 ⌉ x+⌈\frac{d}{x+1}⌉ x+⌈x+1d⌉能否小于 n n n.
对于 x + d x + 1 x+\frac{d}{x+1} x+x+1d,我们转换为 x + 1 + d x + 1 − 1 x+1+\frac{d}{x+1}-1 x+1+x+1d−1
我们根据均值不等式可知,当 x + 1 = d x + 1 x+1=\frac{d}{x+1} x+1=x+1d时,可以得到上式得最小值
即 x = d − 1 x=\sqrt{d}-1 x=d−1时
#pragma comment(linker, "/STACK:102400000,102400000")
#include F. Yet Another Meme Problem
Try guessing the statement from this picture http://tiny.cc/ogyoiz.
You are given two integers A A A and B B B, calculate the number of pairs ( a , b ) (a,b) (a,b) such that 1 ≤ a ≤ A , 1 ≤ b ≤ B 1≤a≤A, 1≤b≤B 1≤a≤A,1≤b≤B, and the equation a ⋅ b + a + b = c o n c ( a , b ) a⋅b+a+b=conc(a,b) a⋅b+a+b=conc(a,b) is true; c o n c ( a , b ) conc(a,b) conc(a,b) is the concatenation of a a a and b b b (for example, c o n c ( 12 , 23 ) = 1223 , c o n c ( 100 , 11 ) = 10011 conc(12,23)=1223, conc(100,11)=10011 conc(12,23)=1223,conc(100,11)=10011). a a a and b b b should not contain leading zeroes.
Input
The first line contains t ( 1 ≤ t ≤ 100 ) t (1≤t≤100) t(1≤t≤100) — the number of test cases.
Each test case contains two integers A A A and B ( 1 ≤ A , B ≤ 1 0 9 ) B (1≤A,B≤10^9) B(1≤A,B≤109).
Output
Print one integer — the number of pairs ( a , b ) (a,b) (a,b) such that 1 ≤ a ≤ A , 1 ≤ b ≤ B 1≤a≤A, 1≤b≤B 1≤a≤A,1≤b≤B, and the equation a ⋅ b + a + b = c o n c ( a , b ) a⋅b+a+b=conc(a,b) a⋅b+a+b=conc(a,b) is true.
Example
Input
3
1 11
4 2
191 31415926
Output
1
0
1337
题解
我们考虑这个 c o n c ( a , b ) conc(a,b) conc(a,b),其值就相当于 a ⋅ 1 0 n + b a\cdot 10^n+b a⋅10n+b
那么对于 a ⋅ b + a + b = a ⋅ 1 0 n + b a\cdot b+a+b=a\cdot 10^n+b a⋅b+a+b=a⋅10n+b
化简就得到了 a ( b + 1 ) = a ⋅ 1 0 n a(b+1)=a\cdot 10^n a(b+1)=a⋅10n
我们可以得到 b = 1 0 n − 1 b=10^n-1 b=10n−1
而 a a a得取值便为 A A A得范围, b b b得取值为 9 , 99 , 999... 9,99,999... 9,99,999...
#pragma comment(linker, "/STACK:102400000,102400000")
#include G. HQ9+
HQ9+ is a joke programming language which has only four one-character instructions:
- “H” prints “Hello, World!”,
- “Q” prints the source code of the program itself,
- “9” prints the lyrics of “99 Bottles of Beer” song,
- “+” increments the value stored in the internal accumulator.
Instructions “H” and “Q” are case-sensitive and must be uppercase. The characters of the program which are not instructions are ignored.
You are given a program written in HQ9+. You have to figure out whether executing this program will produce any output.
Input
The input will consist of a single line p which will give a program in HQ9+. String p will contain between 1 and 100 characters, inclusive. ASCII-code of each character of p will be between 33 (exclamation mark) and 126 (tilde), inclusive.
Output
Output “YES”, if executing the program will produce any output, and “NO” otherwise.
Examples
Input
Hi!
Output
YES
Input
Codeforces
Output
NO
Note
In the first case the program contains only one instruction — “H”, which prints “Hello, World!”.
In the second case none of the program characters are language instructions.
题解
如题所述,包含’H’,‘Q’,和9得时候就输出YES
#pragma comment(linker, "/STACK:102400000,102400000")
#include H. Rolling The Polygon
Bahiyyah has a convex polygon with n n n vertices P 0 , P 1 , ⋯ , P n − 1 P_0,P_1,⋯,P_{n−1} P0,P1,⋯,Pn−1 in the counterclockwise order. Two vertices with consecutive indexes are adjacent, and besides, P 0 P_0 P0 and P n − 1 P_{n−1} Pn−1 are adjacent. She also assigns a point Q Q Q inside the polygon which may appear on the border.
Now, Bahiyyah decides to roll the polygon along a straight line and calculate the length of the trajectory (or track) of point Q Q Q.
To help clarify, we suppose P n = P 0 , P n + 1 = P 1 P_n=P_0,P_{n+1}=P_1 Pn=P0,Pn+1=P1 and assume the edge between P 0 P_0 P0 and P 1 P_1 P1 is lying on the line at first. At that point when the edge between P i − 1 P_{i−1} Pi−1 and P i P_i Pi lies on the line, Bahiyyah rolls the polygon forward rotating the polygon along the vertex P i P_i Pi until the next edge (which is between P i P_i Pi and P i + 1 P_{i+1} Pi+1) meets the line. She will stop the rolling when the edge between P n P_n Pn and P n + 1 P_{n+1} Pn+1 (which is same as the edge between P 0 P_0 P0 and P 1 P_1 P1) meets the line again.
Input
The input contains several test cases, and the first line is a positive integer T T T indicating the number of test cases which is up to 50.
For each test case, the first line contains an integer n ( 3 ≤ n ≤ 50 ) n (3≤n≤50) n(3≤n≤50) indicating the number of vertices of the given convex polygon. Following n lines describe vertices of the polygon in the counterclockwise order. The i-th line of them contains two integers x i − 1 x_{i−1} xi−1 and y i − 1 y_{i−1} yi−1, which are the coordinates of point P i − 1 P_{i−1} Pi−1. The last line contains two integers x Q x_Q xQ and y Q y_Q yQ, which are the coordinates of point Q Q Q.
We guarantee that all coordinates are in the range of − 1 0 3 −10^3 −103 to 1 0 3 10^3 103, and point Q Q Q is located inside the polygon or lies on its border.
Output
For each test case, output a line containing Case #x: y, where x is the test case number starting from 1, and y is the length of the trajectory of the point Q rounded to 3 places. We guarantee that 4-th place after the decimal point in the precise answer would not be 4 or 5.
Example
Input
4
4
0 0
2 0
2 2
0 2
1 1
3
0 0
2 1
1 2
1 1
5
0 0
1 0
2 2
1 3
-1 2
0 0
6
0 0
3 0
4 1
2 2
1 2
-1 1
1 0
Output
Case #1: 8.886
Case #2: 7.318
Case #3: 12.102
Case #4: 14.537
题解
这个题的意思就是给一个凸包,凸包里面有个点,我们滚动这个凸包,问这个点它走过的路径是多少
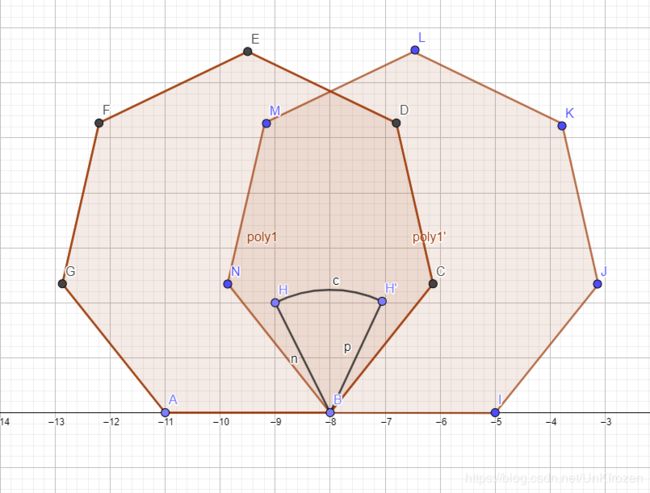
拿这个图说吧,就是 A B AB AB转到了 N B NB NB的位置, B C BC BC转到了 B I BI BI的位置
我们可以知道 ∠ A B N = ∠ C B I = ∠ H B H ′ \angle{ABN}=\angle{CBI}=\angle{HBH'} ∠ABN=∠CBI=∠HBH′,毕竟旋转的角度是一样的啊
然后咧,我们求 H H ′ ⌢ \overset{\frown}{HH'} HH′⌢的长度,就相当于求圆弧嘛.
以 B B B为圆点, ∠ H B H ′ \angle{HBH'} ∠HBH′的角所对应嘛
然后求 ∠ H B H ′ \angle{HBH'} ∠HBH′相当于求 ∠ A B N \angle{ABN} ∠ABN相当于求 π − ∠ N B I \pi-\angle{NBI} π−∠NBI
然后就结束了
#pragma comment(linker, "/STACK:102400000,102400000")
#include