QLU ACM 2018新生赛解题报告

A [1303]约数个数

题目描述

  p^q表示p的q次方，正整数M可以分解为M=( p_1^a_1 )(p_2^a_2)(p_3^a_3)……(p_n^a_n)的形式，其中p_1，p_2……p_n为质数(大于1并且只能被1和自身整除的数叫做质数)。a_1，a_2……a_n为整数。例如18=(2¹)(3²)，45=(3²)(5¹)。
  给出n和一个质数g，以及正整数M分解后的形式，求M的所有约数中，有多少能被g整除。

输入

第一行 两个数n和g.0 第二行 n个数p_1到p_n ,1 第三行 n个数a_1到a_n,0<=a_i<=20,a_i为整数（1<=i<=n）。
保证对于任意的i,j(i != j) ,p_i != p_j

输出

一个数
表示M的所有约数中，有多少能被g整除。

样例输入
2 3
3 5
2 2

样例输出
6

提示
样例解释：
M=(3²)(5²)=9x25=225
225能被3整除的约数有3 9 15 45 75 225 共6个。

解析

  基础数论题目,及一个数,可以分解为多个质数的次方积的形式,并且每个数分解的方式且唯一.
  也就是算术基本定理.
  知道这个定理后,那么得到的质数g,只需判断该数是否在分解的式子里存在并且质数大于0即可.
设p=(g^b)(c^d),那么可以整除g的有(g¹,g²,g³…g^b)(c⁰,c¹…,c^d)种,也就是b*(d+1)
(注,这里质数大于0是个坑点…我在这里wa了7次)

#include
#include
#include

int a[110], b[110];
int main()
{
	int n, g;
	long long sum = 1;  //为了防止乘积卡int
	scanf("%d %d",&n,&g);
	for (int i = 0; i < n; i++)   //输入有哪些质因数
		scanf("%d",&a[i]);
	for (int i = 0; i < n; i++)  //借助桶排序的思想,将每个质因数所对应的指数储存
		scanf("%d",&b[a[i]]);
	if (b[g] == 0)   //如果搜索的质数不存在,或指数为0,直接输出0
		printf("0\n");
	else {
		for (int i = 0; i < n; i++)   //计算有多少种结果
			if (b[a[i]] != 0 && a[i] != g)  //这个因数如果不是g,就让他的个数+1后相乘
				sum *= (b[a[i]] + 1);
			else if (a[i] == g)   //如果是g,则直接乘
				sum *= b[g];
		printf("%lld\n",sum);   //输出结果
	}
	return 0;
}

B [1301]Alice and Bob

题目描述

  Alice and Bob decide to play a game. At the beginning of the game they put n piles of sweets on the table.The number of each pile of sweets may be different. Alice and Bob take away sweets in turn,and always Alice takes sweets first in every games.Each time in their turn they can get only one whole pile of sweets.When there is no sweet left, the game is over. Finally, The man who have the largest number of sweets in hand will win.
  Assume that Alice and Bob were very clever.

输入

  The first line is an integer n, which means that there are n pile sweets.1 <= n <= 100000
  Next n integers, the i-th integer means the number of sweets in the i-th pile.
  The number of sweets in each pile is less than 10000.

###输出
  If Alice wins, output “A”, and if Bob wins, output “B”.
  Otherwise output “again”

样例输入
样例输入1:
3
1 6 7

样例输入2:
4
3 3 3 3

样例输出
样例输出1:
A

样例输出2:
again

解析

  一句话,假的博弈论…比赛的时候没看懂题意,就觉得是轮流取数,是"按照物品的顺序取"还是"不按照物品顺序取"之间纠结,于是就使了下,发现是可以不按顺序取就可以.
英语差,看不懂
  题目大意为,这俩孩儿,轮流拿东西,谁最后手里的总物品价值最大,谁赢.俩孩儿都很聪明,会选择当下最优结果.每次都是Alice先拿女孩儿,然后再是Bob.谁赢,输出谁的名字首字母,平局就输出"again"再来一次.
显然…Bob这个傻孩子是别想赢了.
  先排序,轮流拿,比较最终结果,输出.

#include
#include
#include

int a[100010];
int cmp(const void *a,const void *b)
{
	return *(int *)b-*(int *)a;
}
int main()
{
	int n;
	long long sum1 = 0,sum2=0;
	scanf("%d",&n);
	for (int i = 0; i < n; i++)
		scanf("%d",&a[i]);
	qsort(a,n,sizeof(a[0]),cmp);  //c的qsort函数,可自行百度
	for (int i =0; i<n; i++)
		if (i % 2)  //如果i%2=0,那就是Alice拿,否则就是Bob
			sum2 += a[i];
		else
			sum1 += a[i];
	if (sum1 > sum2)
		printf("A\n");
	else if (sum1 < sum2)
		printf("B\n");
	else
		printf("again\n");
	return 0;
} 

C [1289] 黑白黑

题目描述

  黑白黑是一个很经典的游戏，规则也非常简单。三个人同时伸出一只手，手心为白，手背为黑，如果有两人为黑一人为白，或者两人为白一人为黑，则单独伸出手心或者手背的那个人就输了。
  又是一个周末，小A小B小C他们仨个懒虫又睡到了中午，外卖送到楼下了也不想下楼拿，于是他们决定用这个游戏来选出一个输的人去拿外卖。

输入

三个整数
a b c
(0 <= a,b,c <= 1)
a表示小A
b表示小B
c表示小C
0表示伸出的手背
1表示伸出的手心

输出

如果有人输了则输出他的名字A/B/C（大写）
平局则输出"aha"（不含引号）

样例输入
样例输入1:
0 0 0

样例输入2:
1 1 0

样例输出
样例输出1:
aha

样例输出2:
C

解析

布尔运算直接过
三个if,只要两个相同,一个不同,然后只需要特判到底谁是卧底就可以了.

#include
#include
#include

int main()
{
	int a, b, c;
	scanf("%d %d %d",&a,&b,&c);
	if (a == b && a != c)
		printf("C\n");
	else if (a == c && a != b)
		printf("B\n");
	else if (b == c && b != a)
		printf("A\n");
	else
		printf("aha\n");
	return 0;
}

D [1300]GPA

题目描述

  期末考试成绩终于出来了，小杜怀着忐忑的心情查了一下自己的成绩，还好7门课程都没有挂科。
  不过教务系统出故障了，唯独不显示小杜的平均绩点，但是小杜这种学渣又不会算，你能帮他计算一下吗？

输入

第一行输入7个整数 分别为这7门课程的成绩
第二行输入7个整数 分别为这7门课程的学分
0 <= 成绩 <= 100
1 <= 学分 <= 5
成绩与学分均为整数

输出

输出一行，即小杜的平均绩点，保留2位有效数字

样例输入
67 80 69 60 94 100 80
1 2 4 4 3 2 1

样例输出
2.29

对于样例的解释：
(1.5* 1+2.5* 2+1.5* 4+1.0* 4+4.0* 3+4.0* 2+2.5* 1)/(1+2+4+4+3+2+1) = 2.2941176470588

提示
成绩 绩点
91-100 4.0
86-90 3.5
81-85 3.0
76-80 2.5
71-75 2.0
66-70 1.5
60-65 1.0
60以下 0
平均绩点:(课程学分1* 绩点+课程学分2* 绩点+…+课程学分n*绩点)/(课程学分1+课程学分2+…+课程学分n)

解析

根据提示,一点点写if就完事了=^=

#include
#include

double a[2][8];
int main()
{
	double sum = 0,ans=0;
	for(int i=0;i<2;i++)
		for (int j = 0; j < 7; j++)
			scanf("%lf",&a[i][j]);
	for(int i=0;i<7;i++){
		ans += a[1][i];
		if (a[0][i] > 90 && a[0][i] <= 100)
			sum += 4.0*a[1][i];
		else if (a[0][i] <= 90 && a[0][i] > 85)
			sum += 3.5*a[1][i];
		else if (a[0][i] <= 85 && a[0][i] > 80)
			sum += 3.0*a[1][i];
		else if (a[0][i] <= 80 && a[0][i] > 75)
			sum += 2.5*a[1][i];
		else if (a[0][i] <= 75 && a[0][i] > 70)
			sum += 2.0 * a[1][i];
		else if (a[0][i] <= 70 && a[0][i] > 65)
			sum += 1.5*a[1][i];
		else if (a[0][i] <= 65 && a[0][i] >= 60)
			sum += 1.0*a[1][i];
	}
	printf("%.2f\n", sum / ans);
	return 0;
}

E [1302]are you ok?

题目描述

  小朋是一家超市的老板,他经常会来超市检查,每次都会让仓库管理员列出仓库中剩余商品的数量。但是仓库管理员是个非常健忘的人，有时候商品都卖光了也不去进货，这会让老板非常生气，因为这样超市卖不出去东西就没办法赚钱了。小朋有句口头禅"are you ok?"，如果发现所有商品的库存都为0的话，就会非常生气地喊出"are you ok?"，大声地质询仓库管理员。
  现在你就是仓库管理员，每次面对小朋的询问，你都会在电脑系统中对库存进行查询，然后列出剩余商品的清单。（如果所有商品库存都是0，那你就没办法交差了，你的老板会非常生气）。

输入

第一行一个整数n，表示有n种货物
(2 <= n <= 100)
往下一行有n个字符串s1,s2…si…sn 表示系统显示的第i种货物的名称（1<=i<=n）
(字符串长度不超过10)
往下一行有n个整数a1,a2…ai…an 表示系统显示的第i种货物的库存（1<=i<=n）
(每种货物库存数量 <= 1000)

输出

如果还有商品（哪怕只有一个），你也可以列出剩余商品的清单。
否则你就只能挨老板骂了。

样例输入
样例输入1:
4
a b c d
0 0 0 0

样例输入2:
5
apple egg milk desk light
0 1 2 0 1

样例输出
样例输出1:
are you ok?

样例1的说明：
所有的商品都没库存， 你的老板会非常生气

样例输出2:
egg x 1
milk x 2
light x 1
(x前后有空格)

解析

循环一遍,只要有个东西有库存,就令f=1,及不用输出are…,如果f=0,也就是没库存,就输出are you…

#include
#include
#include

struct vec {
	char s[110];
	int x;
}p[100];
int main()
{
	int n,f=0;
	scanf("%d",&n);
	for (int i = 0; i < n; i++)
		scanf("%s",&p[i].s);
	for (int i = 0; i < n; i++)
		scanf("%d",&p[i].x);
	for (int i = 0; i < n; i++)
		if (p[i].x != 0) {
			printf("%s x %d\n",p[i].s,p[i].x);
			f = 1;
		}
	if(!f)
		printf("are you ok?\n");
	return 0;
}

F [1290]折纸达人

题目描述

  小明最近对折纸很感兴趣，他想知道一张正方形的纸在多次折叠以后沿纸的中线用剪刀将其剪开能得到多少张纸？

输入

第一行一个整数t,表示一共有t组数据(1 <= t <= 100)
每组输入数据包括三行
第一行为一个整数n，表示有n次操作(1 <= n <= 10^5)
  第二行为n个大写字母(四种情况L,R,T,B L表示从左向右折 R表示从右向左折 T表示从上向下折 B表示从下向上折)
  第三行为两个字母(四种情况 LR,RL,TB,BT LR表示从左向右剪 RL表示从右向左剪 TB表示从上往下剪 BT表示从下往上剪)

输出

输出一个整数表示能得到的纸的数目
答案可能过大 需要对1000000007 (1e9+7)取模

样例输入
2

2
BB
LR

1
R
LR

样例输出
5
2

提示
所有的“对折”与“剪”的操作均沿中线进行

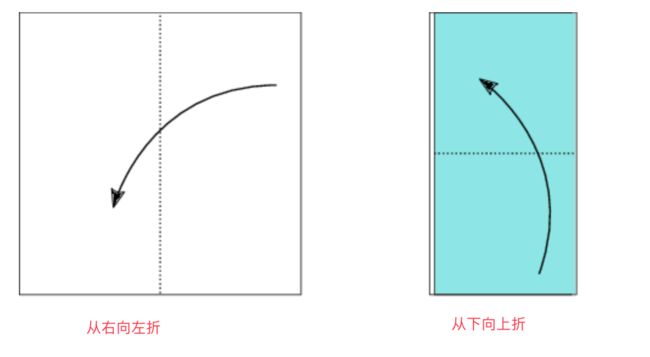
对于样例中第二组数据的解释：

折叠

剪

最终结果

解析

蒟蒻我总结规律的能力奇差无比
  在L题三重for循环+线段树无限超时又不想去写别的解法之后,我撕了1h30分钟的纸,emm,应该差不多.还是没做出来╮(╯▽╰)╭.
  今日观苗大佬的讲解才明白过来.早知道就不剪啊剪了╮(╯▽╰)╭
  规律如下:

上下折叠只对左右剪有关
左右折叠只对上下剪有关
向上折叠和向下折叠是一样的,向左或者向右剪相同
向左折叠和向右折叠是一样的,向上或者向下剪相同
个数问题,向一个方向剪,那么纸数为另一方向的折叠数 ,k次折叠,则值为2^k+1

总结东西好难啊

#include
#include
#include

const long long Mod = 1000000007;
char s[100010],c[3];
int main()
{
	int t;
	scanf("%d", &t);
	while (t--)
	{
		int lr=0, tb=0,n;
		long long ans = 1;
		scanf("%d%s", &n, &s);
		for (int i = 0; i < strlen(s); i++)
			if (s[i] == 'R' || s[i] == 'L')
				lr++;
			else
				tb++;
		scanf("%s", &c);
		if (strcmp(c,"LR")==0||strcmp(c,"RL")==0)
			for (int i = 1; i <= tb; i++)
				ans = ans * 2 % Mod;     //注意每次都要%一次,防止超,这里可以参看同余定理
		else
			for (int i = 1; i <= lr; i++)
				ans = ans * 2 % Mod;
		ans++;
		printf("%lld\n",ans);
	}
	return 0;
}

G [1299]数数

题目描述

  小凯今年上一年级了，他只学会了0-9这十个数字，对于两位以上的数字，小凯自创了一套读法。
  连续出现的x个y,小凯将其读作“xy”
  比如:11 小凯读作"21" (连续2个1)
  21 小凯读作"1211" (连续1个2 连续1个1)
  99 小凯读作"29" (连续2个9)
  310 小凯读作"131110"(连续1个3 连续1个1 连续1个0)
  330111 小凯读作"231031"(连续2个3 连续1个0 连续3个1)
  给定一个由数字组成的字符串n(2 <= |n| <= 100),请输出小凯对n的读法
  |n|表示字符串n的长度
  保证连续出现同一个数字的次数不会超过9次(因为小凯最多只能数到9)
  比如:2223311111111118(非法,因为数字1连续出现了10次)

输入

  由纯数字组成的一行字符串

输出

  在小凯的自创规则下这一长串数的读法

样例输入
13145

样例输出
1113111415

解析

  当作一个字符串处理就可以了,当数到第i位数时,如果这位数和第i-1的数不一样,那么就输出数的个数和这个数

#include
#include
#include

char s[110];
int main()
{
	int sum=0;
	scanf("%s",&s);
	char x = s[0];
	for (int i = 0; i < (int)strlen(s); i++) {
		if (x == s[i])
			sum++;
		else {
			printf("%d%c",sum,x);
			x = s[i];
			sum = 1;
		}
	}
	printf("%d%c\n",sum,x);
	return 0;
}

H [1291]老虎机

题目描述

  不知道你有没有玩过老虎机，现在小明面前有一台神奇的老虎机，这台机器有n个滚轮，从左往右数第i个滚轮包含1到a_i的整数(包括1和a_i)。在按下按钮之后，所有的滚轮都会飞速旋转，最终停下来，每个滚轮将显示其中一个整数。这个过程是随机的。小明有一个有趣的想法，如果将滚轮显示的数字连接起来看做一长串字符串的话，将会有非常多的可能，在这所有的可能中字典序最小的字符串是哪个？（只能从左向右读）

  对于字典序的说明:
  两个字符串S和T，从前往后比较，如果存在一个位置，在该位置两个字符串的字符不同，则比较小的那个所在的字符串字典序更小。
  例如: 123的字典序比14的小，因为在第二个位置上2小于4
12345的字典序比9的小
220的字典序比22的大，因为22是220的一个前缀

输入

一个整数t，表示有t组数据(1 <= t <= 100)
每组第一行为一个整数n表示老虎机有n个滚轮
(1 <= n <= 1000)
第二行为n个整数（a_1 a_2 … a_i … a_n ）
表示第i个滚轮上的数字范围(1~a_i)
(1 <= a_i <= 100)

输出

每组输入对应一行输出，输出字典序最小时老虎机滚轮上显示的数字
两个数字之间用空格隔开

样例输入
2
4
6 6 6 6
2
2 2

样例输出
1 1 1 1
1 1

提示
老虎机上显示的数都不含前导0
比如：某一块滚轮包含[1,33]，如果它显示"1"的话，显示的是"1"而不是"01"

对于样例2的解释:
所有情况分别为：“1 1”、“1 2”、“2 1”、“2 2”
其中"1 1"是字典序最小的，所以答案为"1 1"

解析

前n-1位的数字零越多越好,最后一位越小越好.
啥意思??
1 1和
100 1比较,显然100 1小
1 10 1 100和
1 10 1 1比较,显然1 10 1 1小

#include
#include
#include

int a[1100], b[110];
int main()
{
	int n, t;
	scanf("%d",&t);
	while(t--){
		scanf("%d",&n);
		for (int i = 1; i <= n; i++)
			scanf("%d",&a[i]);
		for (int i = 1; i < n; i++)
			if (a[i] < 10)
				printf("1 ");
			else if (a[i] < 100)
				printf("10 ");
			else if (a[i] == 100)
				printf("100 ");
		printf("1\n");
	}
}

I [1293]五环

题目描述

  提到五环，我想大家都非常熟悉。“啊_{五环你比四环多一环}~~”
  不好意思 跑题了。。。
  奥运五环由蓝、黄、黑、绿、红五种颜色的圆环组成。
  小迪认为五个圆环分别代表五大洲：
蓝色 = 欧洲
黄色 = 亚洲
黑色 = 非洲
绿色 = 大洋州
红色 = 美洲
对应英文为
Blue = Europe
Yellow = Asia
Black = Africa
Green = Oceania
Red = America

输入

输入一行字符串
字符串为五环的颜色或者五个大洲的名称

输出

如果输入的是颜色则输出对应的大洲
如果输入的是大洲则输出对应的颜色

样例输入
Blue

样例输出
Europe

解析

这个题啊…乖乖打个表吧,然后再搬出c的利器strcmp,相同返回1.返回-1和0是什么情况可以自行百度

#include
#include
#include

char a[5][9] = { "Blue","Yellow","Black","Green","Red" };
char b[5][9] = { "Europe","Asia","Africa","Oceania","America" };
int main()
{
	char c[9];
	scanf("%s",&c);
	for (int i = 0; i < 5; i++)
		if (strcmp(a[i], c)==0)
			printf("%s\n", b[i]);
	for (int i = 0; i < 5; i++)
		if (strcmp(b[i], c)==0)
			printf("%s\n",a[i]);
	return 0;
}

J [1296]开挂的小洋

题目描述

  最近小洋迷上了一款名叫打地鼠的游戏,但是小洋是个游戏白痴,这么简单的游戏也总是得不到几分,有一天他发现这款游戏可以在网络上买到外挂,这款外挂可以提前预知所有地鼠出现的时间,并且他可以开局得到两把锤子,之前小洋1s只能挥动一次锤子,现在他左右开弓可以同时打中最多两只地鼠。每只地鼠在第i秒出现,在第i+1秒的时候就会消失。也就是说在第i秒小洋只能打到这一秒出现的地鼠,(i-1)秒以及(i+1)秒出现的地鼠他都没办法打中。

输入

一个整数n,表示地鼠的数目
一个整数m,表示此次游戏时长
接下来n个整数a_1-a_n,表示地鼠会在第a_i秒出现
1 <= a_i <= m
1 <= n <= 1000;
1 <= m <= 100000;
每只地鼠最多停留一秒

输出

一个整数,表示小洋最高得分（每打中一只地鼠得一分）

样例输入
样例输入1:
4
9
1 1 4 7

样例输入2:
6
10
3 3 3 3 9 1

样例输出
样例输出1:
4

样例输出2:
4

提示
对于样例1的解释：
第1秒出现两只地鼠 左右开弓两只全打中得2分
第4秒出现一只地鼠 打中得1分
第7秒出现一只地鼠 打中得1分
最终得分4分

对于样例2的解释:
第1秒出现一只地鼠 打中得1分
第3秒出现四只地鼠 两把锤子最多打中两只 得2分
第9秒出现一只地鼠 打中得1分
共4分

解析

借助桶排序的思想,把第i秒地鼠的个数全都存在第i个元素上

#include
#include

int a[100010];
int main()
{
	int n, m,sum=0,maxx=0;
	scanf("%d %d",&n,&m);
	for (int i = 0; i < n; i++) {
		int x;
		scanf("%d",&x);
		maxx = maxx>x?maxx:x;  //最晚出现的时间,减少遍历的个数
		a[x]++;   //储存
	}
	for (int i = 1; i <=maxx; i++)
		if (a[i] > 2)  //一次只能最多打俩
			sum += 2;
		else
			sum += a[i];
	printf("%d\n",sum);
	return 0;
}

K 数字匹配

题目描述

  给出两个元素数量都为n的数组a和数组b。对于数组a中的每个元素，都必须找一个（而且最多一个）数组b中的元素进行匹配，数组b中的所有元素也都要被匹配到,也就是说一一匹配。匹配完成后，相互匹配的元素相乘，然后把所有的积相加。
例如：
数组a：1 5 3
数组 b：2 3 4
  如果a中第一个元素跟b中第三个元素匹配，第二个元素跟b中第二个元素匹配，第三个元素跟b中第一个元素匹配，匹配完后相乘得到 14、53、32，求和得到结果14+53+32=25。
  如果a中第一个元素跟b中第二个元素匹配，第二个元素跟b中第三个元素匹配，第三个元素跟b中第一个元素匹配，匹配完后相乘得到 13、54、32，求和得到结果13+54+32=29。
  给出n和两个数组，分别计算求和的最大结果与最小结果。

输入

第一行 一个数n，表示两个数组元素的个数 1<=n<=1000。
第二行 n个数 表示数组a的各个元素ai，0 第三行 n个数 表示数组b的各个元素bi，0

输出

两个数 分别表示最大结果和最小结果。最大结果和最小结果可以相等。

样例输入
3
1 5 3
2 3 4

样例输出
31 23

解析

emmm,一道经典的数学题,公式结论,可翻看高中数学选修<不等式选讲>,排序不等式

//将两个数组正序排后相乘求和为最大值
//一个正序,一个逆序,相乘求和为最小值
//结束
#include
#include
#include

int a[10010], b[10010];
int cmp(const void *a,const void *b)
{
	return *(int *)a-*(int *)b;
}
int main()
{
	int n,sum1=0,sum2=0;
	scanf("%d",&n);
	for (int i = 0; i < n; i++)
		scanf("%d",&a[i]);
	for (int i = 0; i < n; i++)
		scanf("%d",&b[i]);
	qsort(a,n,sizeof(a[0]),cmp);
	qsort(b,n,sizeof(b[0]),cmp);
	for (int i = 0; i < n; i++) {
		sum1 += a[i] * b[i];
		sum2 += a[i] * b[n - 1 - i];
	}
	printf("%d %d\n",sum1,sum2);
	return 0;
}

L [1298]寄蒜几何

题目描述

  现在有一个圆圈，圆圈上有若干个点，请判断能否在若干个点中选择三个点两两相连组成一个等边三角形？
  这若干个点在圆圈上按顺时针顺序分布。
  如果可以的话输出"Yes"(不含引号)
  不可以的话输出"No"(不含引号)

输入

  第一行一个整数n，表示圆圈上有n个点
  第二行n个整数，分别表示第1个点与第2个点之间圆弧的长度、第2个点与第3个点之间圆弧的长度······第n个点与第1个点之间圆弧的长度
3 <= n <= 10^6
1 <= x_i <= 1000 ( 1 <= i <= n)

输出

如果可以组成等边三角形则输出"Yes"(不含引号)
否则输出"No"(不含引号)

样例输入
样例输入1：
4
1 1 2 2

样例输入2：
8
4 2 4 2 2 6 2 2

样例输出
样例输入1：
Yes

样例输入2：
Yes

提示
对于样例2配图：

解析

  仔细读题,要求写在一个圆里面找一个等边三角形,有就输出Yes,没有就输出No.
  emm,选择一个等边三角形,就等于找到三个圆弧长度相同.
  那就从i点寻找,找到点j,使得点s[i~j]=圆周长的1/3,然后再从j点搜索,找到k点,使得s[j ~k]=圆的周长的1/3.那么可以知道s[k ~i]必定等于圆的周长1/3.
  嗯,我真机智.三个for循环嘛不就是,emmm,完美超时38%,nice 别告诉我数据范围10^6
  转念一想,哦,求区间长度,那不就用线段树降复杂度吗,我不会树状数组
  然后手搓线段树,提交,超时18%,嗯,优秀…
  等等,求一个按照小到大排列的区间,用二分搜索不就快吗~ ~
  终于成功AC.嗯,耗时171ms. 我不喜欢用c++的map
  具体线段树的定义,c/c++的写法,可以看这里浅谈线段树的指针写法

#include
#include
#include
#ifndef NULL
#define NULL 0
#endif

typedef struct Segment_Tree* Node;
typedef long long ll;
struct Segment_Tree {
   ll d;
   int left, right;
   Node lson, rson;
}*root;
int a[1000010], n;
ll s;
Node built(int left, int right)
{
   Node p = (Node)malloc(sizeof(Segment_Tree));
   p->left = left;
   p->right = right;
   if (left == right) {
   	p->d = a[left];
   	p->lson = NULL;
   	p->rson = NULL;
   }
   else {
   	int mid = (left + right) / 2;
   	p->lson = built(left, mid);
   	p->rson = built(mid + 1, right);
   	p->d = p->lson->d + p->rson->d;
   }
   return p;
}
ll find(Node p, int x, int y)  //区间查找
{
   if (p->left == x && p->right == y)
   	return p->d;
   int mid = (p->left + p->right) / 2;
   if (y <= mid)
   	return find(p->lson, x, y);
   if (x > mid)
   	return find(p->rson, x, y);
   return find(p->lson, x, mid) + find(p->rson, mid + 1, y);
}
void close(Node p)
{
   if (p != NULL) {
   	close(p->lson);
   	close(p->rson);
   	free(p);
   }
   return;
}
int Binary_Search(int i,int left, int right)   //二分查找
{
   while (left < right) {
   	int mid = (left + right) / 2;
   	ll t = find(root, i, mid);
   	if (t > s)
   		right = mid;
   	else if (t < s)
   		left = mid + 1;
   	else
   		return mid;
   }
   return -1;
}
int main()
{
   scanf("%d",&n);
   for (int i = 1; i <= n; i++)  //存数据
   	scanf("%d", &a[i]);
   root = built(1, n);
   s = root->d / 3;
   for (int i = 1; i <= n; i++) {  //假定第一个点i
   	int j = Binary_Search(i,i, n)+ 1;  //二分查找,符合s[i~j]=s的j
   	if (j == 0)
   		continue;
   	else if(Binary_Search(j,j,n)!=-1){   //二分查找,符合s[j~k]=s的点,找到了立刻结束程序,减少耗时
   		printf("Yes\n");
   		exit(0);
   	}
   }
   printf("No\n");  //找不到say no
   close(root);
   return 0;
}

M [1318]签到题

题目描述

  恭喜你发现一道签到题，请输出“check in”来解决这道问题。

输入

无

输出

check in

样例输入
无

样例输出
check in

提示
恭喜你，签到成功

解析

=^=

#include
#include

int main()
{
	printf("check in\n");
	return 0;
}