无向图的关节点和重连通分量

     以下内容主要参考了严蔚敏版的数据结构教材。我觉得教材在算法原理方面讲解的不是那么通俗易懂，所以我同时也参考了这个文档，它在算法原理方面的讲解要通俗易懂一些，可以作为教材的一个补充。
     以下讲解针对的是连通的无向图。如果删除连通的无向图中的一个顶点V以及和顶点V相关的边后可以将连通的无向图分割成两个或两个以上的连通分量则顶点V为该无向连通图的关节点。一个没有关节点的连通的无向图称为重连通图。图1是一个连通的无向图，它有关节点$A、B、D、G$。

　 图1.

     利用深度优先遍历可以求连通图的关节点。图2是图1的无向图的深度优先生成树。图中实线是深度优先搜索过程走过的图中的边，虚线是深度优先搜索过程没有走过的图中的边。对生成树中任一顶点V而言，其孩子节点为在它之后搜索到的邻接点，其双亲节点和由回边（生成树中的虚线）连接的祖先节点是在它之前搜索到的邻接点。由深度优先生成树可以得到两类关节点的特性：

1. 如果生成树的根有两个或两个以上的子树，则此根节点必为关节点。因为此时不存在连接不同子树中的节点的边，因此删除根节点生成树便会称为生成森林。
2. 如果生成树中某个非叶子节点V，其某颗子树的根以及该子树中的其它节点没有指向节点V的祖先的回边，则V为关节点。因为此时删除节点V则该子树和图的其它部分分开来。

     求关节点的算法中使用了两个辅助数组$nodeVisitedOrderNumber$和$low$。数组$nodeVisitedOrderNumber$用来记录每一个节点在深度优先搜索过程中被搜索到的次序。如果$nodeVisitedOrderNumber[3]=7$则说明搜索到节点3（从0开始计数）时前面已经搜索到了6个节点。生成树中对于某个节点V的所有子树中的每一个节点$v_x$，假设和它相关的边有n个，相应的节点为$v_{x_1}$、$v_{x_2}$、…、$v_{x_n}$，这些节点在深度有点搜索过程中的搜索次序号分别为$s_1$、$s_2$、…、$s_n$，假设这n个搜索次序号中最小的为$s_i$。现在假设节点V的所有子树中一共有m个节点，这m个节点的$s_i$值的最小值即为数组$low$中与节点V对应的元素的值。数组$low$中各元素值的求解方法：$low[v]=Min\{visited[v],low[w],visited[w]\}$，节点w是顶点v在深度优先生成树中的孩子节点，节点k是顶点v在深度优先生成树上由回边连接的祖先节点，边$<v,w>$和边$<v,k>$都是无向图中实际存在的边。数组$low$中对应的节点的的元素的计算顺序是按照生成树中节点的后续遍历迅速逐一计算的。
     如果对于某个除生成树根节点之外的节点v，存在孩子节点w且$low[w]>=visited[v]$则说明节点v的以w节点为根的子树中的所有节点都没有指向节点v的祖先的边，因此可以得到节点v为关节点。

　 图2.

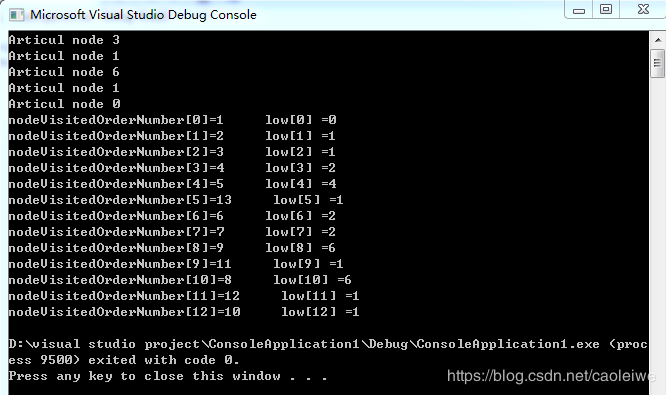
     图3为在图1上的测试结果。因为此时节点0即节点A是生成树的根节点，其实这时不用管它的LOW值，只看它是否有多个子树来判断其是否是关节点。

　 图3.

//图的邻接表表示
//弧节点
class GraphArcNode
{
private:
	int weight;
	int adjVertexIndex;
	GraphArcNode* nextArcNode;
public:
	GraphArcNode(int d = 0, int index = 0)
	{
		weight = d;
		adjVertexIndex = index;
		nextArcNode = nullptr;
	}
	void setNextArcNode(GraphArcNode* next)
	{
		nextArcNode = next;
	}
	int getWeight()
	{
		return weight;
	}
	int getAdjVertexIndex()
	{
		return adjVertexIndex;
	}
	GraphArcNode* getNextArcNode()
	{
		return nextArcNode;
	}
};
//图节点
class GraphNode
{
private:
	int data;
	GraphArcNode* nextArcNode;
public:
	GraphNode(int d = 0)
	{
		data = d;
		nextArcNode = nullptr;
	}
	void setNextArcNode(GraphArcNode* next)
	{
		nextArcNode = next;
	}
	int getData()
	{
		return data;
	}
	GraphArcNode* getNextArcNode()
	{
		return nextArcNode;
	}
};
//图的数据结构
class ALGraph
{
private:
	vector<GraphNode> graphNodeSet;
	int nodeNum;
public:
	ALGraph(int num)
	{
		nodeNum = num;
	}
	void addGraphNode(int data)
	{
		graphNodeSet.push_back(GraphNode(data));
	}
	int getGraphNodeNum()
	{
		return nodeNum;
	}
	GraphArcNode* getGraphNodeFirstArc(int nodeIndex)
	{
		return graphNodeSet[nodeIndex].getNextArcNode();
	}
	void setGraphNodeArc(int graphNodeIndex, int weight, int adjVertexIndex)
	{
		if (graphNodeSet[graphNodeIndex].getNextArcNode() == nullptr)
		{
			graphNodeSet[graphNodeIndex].setNextArcNode(new GraphArcNode(weight, adjVertexIndex));
		}
		else
		{
			GraphArcNode* currentArcNode = graphNodeSet[graphNodeIndex].getNextArcNode();
			GraphArcNode* nextArcNode = graphNodeSet[graphNodeIndex].getNextArcNode()->getNextArcNode();
			while (nextArcNode != nullptr)
			{
				currentArcNode = nextArcNode;
				nextArcNode = nextArcNode->getNextArcNode();
			}
			currentArcNode->setNextArcNode(new GraphArcNode(weight, adjVertexIndex));
		}
	}

	void DFSArticul(int startNode, vector<int>& visited, int& count, vector<int>& low)
	{
		int min = ++count;
		visited[startNode] = min;
		int nextAdjVex = 0;
		for (GraphArcNode* p = getGraphNodeFirstArc(startNode); p != nullptr; p = p->getNextArcNode())
		{
			nextAdjVex = p->getAdjVertexIndex();
			if (visited[nextAdjVex] == 0)//节点startNode的该邻接点没有访问
			{
				DFSArticul(nextAdjVex, visited, count, low);
				if (low[nextAdjVex] < min)
				{
					min = low[nextAdjVex];
				}
				if (low[nextAdjVex] >= visited[startNode])
					cout << "Articul node " << startNode << endl;

			}
			else if (visited[nextAdjVex] < min)//节点startNode的该邻接点已访问，且该邻接点是其在生成树上的祖先。
			{
				min = visited[nextAdjVex];
			}
		}
		low[startNode] = min;
	}

	void FindArticul()
	{
		int count = 1;
		vector<int> nodeVisitedOrderNumber(nodeNum, 0);
		vector<int> low(nodeNum, 0);
		nodeVisitedOrderNumber[0] = 1;
		GraphArcNode* p = getGraphNodeFirstArc(0);
		int nextAdjVex = p->getAdjVertexIndex();
		DFSArticul( nextAdjVex, nodeVisitedOrderNumber, count, low);
		if (count < nodeNum)//如果生成树的根节点有多个子树则根节点为关节点
		{
			cout << "Articul node 0" << endl;
			while (p->getNextArcNode() != nullptr)
			{
				p = p->getNextArcNode();
				nextAdjVex = p->getAdjVertexIndex();
				if (nodeVisitedOrderNumber[nextAdjVex] == 0)
				{
					DFSArticul(nextAdjVex, nodeVisitedOrderNumber, count, low);
				}
			}
		}
		for (int i = 0; i < nodeNum; i++)
		{
			cout << "nodeVisitedOrderNumber[" << i << "]=" << nodeVisitedOrderNumber[i] << "     low[" << i << "] =" << low[i] << endl;
		}
	}
};

#define A 0
#define B 1
#define C 2
#define D 3
#define E 4 
#define F 5
#define G 6 
#define H 7
#define I 8
#define J 9
#define K 10
#define L 11
#define M 12
//测试程序
int main()
{
	ALGraph g(13);
	for (int nodeDataIndex = 0; nodeDataIndex < 13; nodeDataIndex++)
	{
		g.addGraphNode(nodeDataIndex);
	}
	g.setGraphNodeArc(A, 0, B);
	g.setGraphNodeArc(A, 0, C);
	g.setGraphNodeArc(A, 0, F);
	g.setGraphNodeArc(A, 0, L);
	g.setGraphNodeArc(B, 0, A);
	g.setGraphNodeArc(B, 0, C);
	g.setGraphNodeArc(B, 0, D);
	g.setGraphNodeArc(B, 0, G);
	g.setGraphNodeArc(B, 0, H);
	g.setGraphNodeArc(B, 0, M);
	g.setGraphNodeArc(C, 0, A);
	g.setGraphNodeArc(C, 0, B);
	g.setGraphNodeArc(D, 0, B);
	g.setGraphNodeArc(D, 0, E);
	g.setGraphNodeArc(E, 0, D);
	g.setGraphNodeArc(F, 0, A);
	g.setGraphNodeArc(G, 0, B);
	g.setGraphNodeArc(G, 0, H);
	g.setGraphNodeArc(G, 0, I);
	g.setGraphNodeArc(G, 0, K);
	g.setGraphNodeArc(H, 0, B);
	g.setGraphNodeArc(H, 0, G);
	g.setGraphNodeArc(H, 0, K);
	g.setGraphNodeArc(I, 0, G);
	g.setGraphNodeArc(J, 0, L);
	g.setGraphNodeArc(J, 0, M);
	g.setGraphNodeArc(K, 0, G);
	g.setGraphNodeArc(K, 0, H);
	g.setGraphNodeArc(L, 0, A);
	g.setGraphNodeArc(L, 0, J);
	g.setGraphNodeArc(L, 0, M);
	g.setGraphNodeArc(M, 0, B);
	g.setGraphNodeArc(M, 0, J);
	g.setGraphNodeArc(M, 0, L);
	g.FindArticul();

}