赫夫曼树和赫夫曼编码

     以下内容主要参考了严蔚敏版的数据结构教材。
     赫夫曼树又叫做最优树，是一类带权路径长度最短的树，这里讨论的是最优二叉树。
     假设现在有n个权值$w_1,w_2,...,w_n$，如何构造一颗有n个叶子节点的二叉树使得二叉树的带权路径长度（${\sum }_{k=1}^n{w}_k\ast l_k$）最小，其中$w_1,w_2,...,w_n$分别是n个叶子节点的权值$l_1,l_2,...,l_n$分别是n个叶子节点的路径长度（即树根到该节点的分支数目）。这样额的二叉树叫做最优二叉树或赫夫曼树。
     构造赫夫曼树的算法如下：

1. 根据给定的n个权值$w_1,w_2,...,w_n$构成n颗二叉树的集合$F=\{T_1,T_2,...,T_n\}$，此时每棵二叉树都只有一个权值为$w_i$的根节点，左右子树均为空。
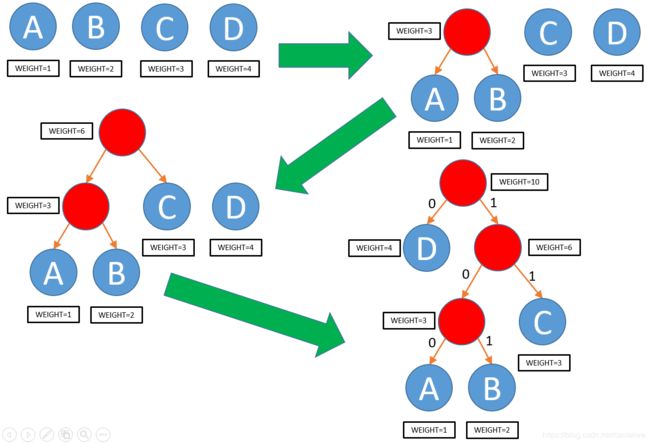
2. 在集合F中选取两颗根节点的权值最小的二叉树作为左右子树构建一颗新的二叉树，新的二叉树的根节点的权值为左右两颗子树的根节点权值的和。
3. 在集合F中删除这两颗二叉树同时将新建立的二叉树加入到集合F中。
4. 重复步骤2和3直到F中只有一颗二叉树时为止。此时即为所求。

     图1是一个简单的例子，测试程序也是在该例子上进行测试的。

　 图1.

     最优二叉树的一个应用是设计二进制前缀编码。前缀编码是一种不等长的编码，对于每个要编码的字符其对应的编码长度不同且每一个字符的编码都不是另一个字符对应的编码的前缀。这样便于译码。可以将出现频率较高的字符编码较少的位数，将出现频率较低的字符编码较多的位数，这样可以使得整体要传送的数据减少，提高了效率。用最优二叉树来设计二进制前缀编码比较简单，将字符出现的频率当做权重，来构建相应的最优二叉树，然后将二叉树左分支的边设为编码’0’，右分支的边设为编码’1’。之后再从根节点到相应叶子节点的字符串就是叶子节点对应的字符的二进制前缀编码。

class HuffmanNode
{
private:
	int weight;
	int parent;
	int leftChild;
	int rightChild;
public:
	HuffmanNode(int d1=0, int d2=0, int d3=0, int d4=0)
	{
		weight=d1;
		parent=d2;
		leftChild=d3;
		rightChild=d4;
	}
	void setWeight(int value)
	{
		weight = value;
	}
	void setParent(int value)
	{
		parent = value;
	}
	void setLeftchild(int value)
	{
		leftChild = value;
	}
	void setRightchild(int value)
	{
		rightChild = value;
	}
	int getWeight()
	{
		return weight;
	}
	int getParent()
	{
		return parent;
	}
	int getLeftchild()
	{
		return leftChild;
	}
	int getRightchild()
	{
		return rightChild;
	}
};

class HuffmanTree
{
private:
	vector<string> HuffmanCodeUp;
	vector<string> HuffmanCodeDown;
	vector<HuffmanNode> treeNodes;
	int LeafNodeNum;
	void selectTwoMininum(vector<HuffmanNode> Nodes,int upperIndex, int &s1,int &s2)
	{
		if (upperIndex < 2)
			return;
		int tempS1 = 0;
		int tempS2 = 0;
		int countParentZero = 0;
		for (int i = 1; i <= upperIndex; i++)
		{
			if ((Nodes[i].getParent() == 0) && (countParentZero == 0))
			{
				tempS1 = i;
				countParentZero++;
			}
			else if ((Nodes[i].getParent() == 0) && (countParentZero == 1))
			{
				tempS2 = i;
				countParentZero++;
				if (Nodes[tempS1].getWeight() > Nodes[tempS2].getWeight())
				{
					int tempIndex = tempS1;
					tempS1 = tempS2;
					tempS2 = tempIndex;
				}
			}
			else if ((Nodes[i].getParent() == 0) && (countParentZero > 1))
			{
				if (Nodes[i].getWeight() <= Nodes[tempS1].getWeight())
				{
					tempS2 = tempS1;
					tempS1 = i;
				}
				else if ((Nodes[tempS1].getWeight() < Nodes[i].getWeight()) && (Nodes[i].getWeight() <= Nodes[tempS2].getWeight()))
				{
					tempS2 = i;
				}
				countParentZero++;
			}
		}
		s1=tempS1;
		s2=tempS2;
		return;
	}
public:
	HuffmanTree(int leafNodeNum,vector<int> leafNodeWeight)
	{
		LeafNodeNum = leafNodeNum;
		treeNodes = vector<HuffmanNode>(2*leafNodeNum, HuffmanNode());
		for (int i = 1; i <= leafNodeNum; i++)
		{
			treeNodes[i].setWeight(leafNodeWeight[i-1]);
		}
	}
	void printCodingUp()
	{
		cout << "HuffmanCodeUp=:" << endl;
		for (int i = 0; i < HuffmanCodeUp.size(); i++)
		{
			cout << "HuffmanCodeUp[i]=" << HuffmanCodeUp[i] << endl;
		}
	}

	void printCodingDown()
	{
		cout << "HuffmanCodeDown=:" << endl;
		for (int i = 0; i < HuffmanCodeUp.size(); i++)
		{
			cout << "HuffmanCodeDown[i]=" << HuffmanCodeDown[i] << endl;
		}
	}
	void printTree()
	{
		for (int i = 1; i < 8; i++)
		{
			cout << "i=" << i << endl;
			cout << "weight=" << treeNodes[i].getWeight() << endl;

			cout << "Parent=" << treeNodes[i].getParent() << endl;

			cout << "Leftchild=" << treeNodes[i].getLeftchild() << endl;

			cout << "Rightchild=" << treeNodes[i].getRightchild() << endl;

		}
	}

	void constructTree()
	{
		if (LeafNodeNum < 2)
			return;
		int minimumNode1 = 0;
		int minimumNode2 = 0;
		string currentCode;
		for (int i = LeafNodeNum + 1; i < (2 * LeafNodeNum); i++)
		{
			selectTwoMininum(treeNodes, i - 1, minimumNode1, minimumNode2);
			treeNodes[minimumNode1].setParent(i);
			treeNodes[minimumNode2].setParent(i);
			treeNodes[i].setLeftchild(minimumNode1);
			treeNodes[i].setRightchild(minimumNode2);
			treeNodes[i].setWeight(treeNodes[minimumNode1].getWeight() + treeNodes[minimumNode2].getWeight());
		}
	}
    //从叶子节点开始求每个字符的HUFFMAN编码
	void HuffmanCodingUp()
	{
		int childIndex = 0;
		int parentIndex = 0;
		string currentCode;
		for (int i = 1; i <= LeafNodeNum; i++)
		{
			for (childIndex=i,parentIndex= treeNodes[i].getParent(); parentIndex!=0; childIndex = parentIndex, parentIndex = treeNodes[parentIndex].getParent())
			{
				if (treeNodes[parentIndex].getLeftchild()== childIndex)
				{
					currentCode = currentCode + "0";
				}
				else
				{
					currentCode = currentCode + "1";
				}
			}
			//因为是从叶子节点开始求每个字符的HUFFMAN编码，求得编码后需要将编码逆序
			reverse(currentCode.begin(), currentCode.end());
			HuffmanCodeUp.push_back(currentCode);
			currentCode.clear();
		}
	}
    //从根节点开始求每个字符的HUFFMAN编码
	void HuffmanCodingDown()
	{
		if (LeafNodeNum < 2)
			return;
		int currentNodeIndex = 2 * LeafNodeNum - 1;
		string currentCodeString;
		vector<HuffmanNode> tempTreeNodes = treeNodes;
		for (int i = 1; i < (2 * LeafNodeNum); i++)
		{
		    //此时weight的值可以看做是节点被访问的次数，初始时都为0且最多被访问两次
			tempTreeNodes[i].setWeight(0);
		}
		while (currentNodeIndex!=0)
		{    
		    //初始时没有被访问，访问完后向左边进发
			if (tempTreeNodes[currentNodeIndex].getWeight()==0)
			{
				tempTreeNodes[currentNodeIndex].setWeight(1);
				if (tempTreeNodes[currentNodeIndex].getLeftchild()!=0)
				{
					currentNodeIndex = tempTreeNodes[currentNodeIndex].getLeftchild();
					currentCodeString.push_back('0');
				}
				//如果一个节点的左右子树都为空则为叶子节点，得到相应节点的编码字符串
				else if (tempTreeNodes[currentNodeIndex].getRightchild() == 0)
				{
					HuffmanCodeDown.push_back(currentCodeString);
				}
			}
			//节点已经被访问过一次，向右边进发
			else if (tempTreeNodes[currentNodeIndex].getWeight() == 1)
			{
				tempTreeNodes[currentNodeIndex].setWeight(2);
				if (tempTreeNodes[currentNodeIndex].getRightchild()!=0)
				{
					currentNodeIndex = tempTreeNodes[currentNodeIndex].getRightchild();
					currentCodeString.push_back('1');
				}
			}
			//节点已经被访问过两次则返回其父节点
			else
			{
			    //下面这一句代码是教材中的，我觉得这里可以删除，因为这个节点不会再访问了
				tempTreeNodes[currentNodeIndex].setWeight(0);
				currentNodeIndex = tempTreeNodes[currentNodeIndex].getParent();
				if(currentNodeIndex!=0)
				{ 
				    currentCodeString.pop_back();
				}
			}
		}
	}
};

//测试程序
int main()
{
	int leafNodeNum = 4;
	vector<int> leafNodeWeight;
	leafNodeWeight.push_back(1);
	leafNodeWeight.push_back(2);
	leafNodeWeight.push_back(3);
	leafNodeWeight.push_back(4);
	HuffmanTree tree(leafNodeNum, leafNodeWeight);
	tree.constructTree();
	tree.HuffmanCodingUp();
	tree.printCodingUp();
	tree.HuffmanCodingDown();
	tree.printCodingDown();
}