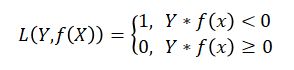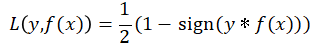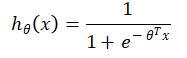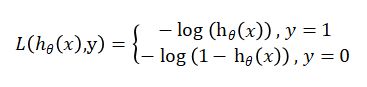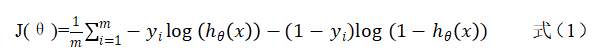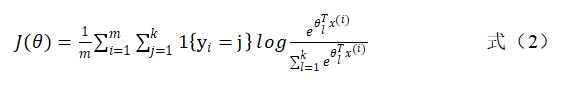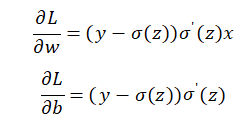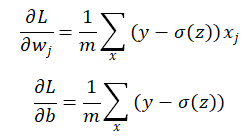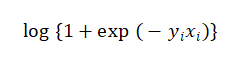深度学习中常见的损失函数
文章来源于AI的那些事儿,作者黄鸿波
2018年我出版了《TensorFlow进阶指南 基础、算法与应用》这本书,今天我把这本书中关于常见的损失函数这一节的内容公开出来,希望能对大家有所帮助。
![]()
在深度学习分类任务中,我们经常会使用到损失函数,今天我们就来总结一下深度学习中常见的损失函数。
0-1损失函数
在分类问题中,可以使用函数的正负号来进行模式判断,函数值本身大小并不重要,该函数衡量的是预测值与真实值的符号是否相同,具体形式如下所示:
其等价于下述函数:
由于0-1损失函数只取决于正负号,是一个非凸的函数,在求解过程中,存在很多的不足,通常在实际应用中使用其替代函数。
对数(Log)损失函数
Log损失函数是0-1损失函数的一种替代函数,其形式如下:
运用Log损失函数的典型分类器是logistic(逻辑)回归算法。为什么逻辑回归不用平方损失呢?原因在于平方损失函数是线性回归在假设样本是高斯分布的条件下推导得到的(为什么假设高斯分布?其实就是依据中心极限定理)。而逻辑回归的推导中,它假设样本服从于伯努利分布(0-1分布),然后求得满足该分布的似然函数,接着求取对数等(Log损失函数中采用log就是因为求解过中使用了似然函数,为了求解方便而添加log,因为添加log并不改变其单调性)。但逻辑回归并没有极大化似然函数,而是转变为最小化负的似然函数,因此有了上式。
已知逻辑函数(sigmoid函数)为:
可以得到逻辑回归的Log损失函数:
上式的含义就是:如果y=1,我们鼓励![]() 趋向于1,
趋向于1,![]() 趋向于0,如果y=1,我们鼓励
趋向于0,如果y=1,我们鼓励![]() 也趋向于0,
也趋向于0,![]() 也趋向于0,即满足损失函数的第二个条件,因为
也趋向于0,即满足损失函数的第二个条件,因为![]() 小于1,为了保证损失函数的非负性,即满足第一个条件,所以添加负号。此时将其合并可得单个样本的损失函数:
小于1,为了保证损失函数的非负性,即满足第一个条件,所以添加负号。此时将其合并可得单个样本的损失函数:
则全体样本的经验风险函数为:
该式就是sigmoid函数的交叉熵,这也是上文说的在分类问题上,交叉熵的实质是对数似然函数。在深度学习中更普遍的做法是将softmax作为最后一层,此时常用的仍是对数似然损失函数,如下所示:
其中![]() 为真时
为真时![]() ,否则为0。
,否则为0。
该式其实是式(1)的推广,正如softmax是sigmoid的多类别推广一样,在TensorFlow里面根据最后分类函数softmax和sigmoid就分为softmax交叉熵以及sigmoid的交叉熵,并对这两个功能进行统一封装。
先看tf.nn.sigmoid_cross_entropy_with_logits(logits,targets)函数,它的实现和之前的交叉熵算法定义是一样的,也是TensorFlow最早实现的交叉熵算法。这个函数的输入是logits和targets,logits就是神经网络模型中的W*X矩阵,注意不需要经过sigmoid,因为在函数中会对其进行sigmoid激活,而targets的shape和logtis相同,就是正确的label值。其计算过程大致如下:
tf.nn.softmax_cross_entropy_with_logits(logits,targets)同样是将softmax和交叉熵计算放到一起了,但是需要注意的是,每个样本只能属于一个类别,即要求分类结果是互斥的,因此该函数只适合单目标的二分类或多分类问题。补充一点,对于多分类问题,例如我们分为5类,并且将其人工编码为0,1,2,3,4,因为输出值是5维的特征,因此需要人工做onehot enconding,即分别编码为00001,00010,00100,01000,10000,才能作为该函数的输入。理论上不做onehot encoding也可以,做成和为1的概率分布也可以,但需要保证和为1,否则TensorFlow会检查这些参数,提醒用户更改。
TensorFlow还提供了一个softmax_cross_entropy_with_logits的易用版本,tf.nn.sparse_softmax_cross_entropy_with_logits(),除了输入参数不同,作用和算法实现都是一样的。softmax_cross_entropy_with_logits的输入必须是类似onehot encoding的多维特征,但像CIFAR-10、ImageNet和大部分分类场景都只有一个分类目标,label值都是从0编码的整数,每次转成onehot encoding比较麻烦,TensorFlow为了简化用户操作,在该函数内部高效实现类似onehot encoding,第一个输入函数和前面一样,shape是[batch_size,num_classes],第二个参数以前必须也是[batch_size,num_classes]否则无法做交叉熵,而这里将其改为[batch_size],但值必须是从0开始编码的int32或int64,而且值的范围是[0,num_class)。如果我们从1开始编码或者步长大于1,则会导致某些label值超过范围,代码会直接报错退出。其实如果用户已经做了onehot encoding,那就可以不使用该函数。
还有一个函数tf.nn.weighted_cross_entropy_with_logits(),是sigmoid_cross_entropy_with_logits的拓展版,输入和实现两者类似,与后者相比,多支持一个pos_weight参数,目的是可以增加或减小正样本在算交叉熵时的loss.其计算原理如下:
还有一个计算交叉熵的函数,sequence_loss_by_example (logits,targets,weights),用于计算所有examples(假设一句话有n个单词,一个单词及单词所对应的label就是一个example,所有examples就是一句话中所有单词)的加权交叉熵损失,logits的shape为[batch_size,num_decoder_symbols],返回值是一个1D float类型的tensor,尺寸为batch_size,其中每一个元素代表当前输入序列example的交叉熵。另外,还有一个与之类似的函数sequence_loss,它对sequence_loss_by_example函数的返回结果进行了一个tf.reduce_sum运算。
值得一提的是,当最后分类函数是sigmoid和softmax时,不采用平方损失函数除上文中提到的样本假设分布不同外,还有一个原因是如果采用平方损失函数,则模型权重更新非常慢,假设采用平方损失函数如下式所示:
采用梯度下降算法调整参数的话,则有
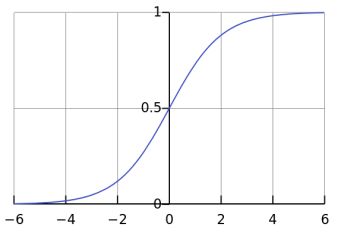
可知w和b的梯度跟激活函数的梯度成正比,但是因为sigmoid的性质,导致![]() 在z取大部分值时都会很小,这样导致w和b更新非常慢,如图所示。
在z取大部分值时都会很小,这样导致w和b更新非常慢,如图所示。
而如果采用交叉熵或者说对数损失函数,则参数更新梯度变为:
可以看到,没有![]() 这一项,权重的更新受误差影响,误差越大权重更新越快,误差越小权重更新就慢,这是一个很好的性质。
这一项,权重的更新受误差影响,误差越大权重更新越快,误差越小权重更新就慢,这是一个很好的性质。
为什么一开始我们说log损失函数也是0-1损失函数的一种替代函数,因为log损失函数其实也等价于如下形式:
Hinge损失函数
Hinge损失函数也是0-1函数的替代函数,具体形式如下:
对可能的输出![]() 和分类器预测值
和分类器预测值![]() , 预测值
, 预测值![]() 的损失就是上式。运用Hinge损失函数的典型分类器是SVM算法,
的损失就是上式。运用Hinge损失函数的典型分类器是SVM算法,![]() 。可以看出当
。可以看出当![]() 和y同符号时,意味着hinge loss为0,但是如果它们的符号相反,
和y同符号时,意味着hinge loss为0,但是如果它们的符号相反, ![]() 则会根据
则会根据![]() 线性增加。
线性增加。
指数损失
具体形式如下:
这也是0-1函数的一种替代函数,主要用于AdaBoost算法。
感知机损失
这也是0-1函数的一种替代函数,具体形式如下:
运用感知机损失的典型分类器是感知机算法,感知机算法只需对每个样本判断其是否分类正确,只记录分类错误的样本,类似hinge损失,不同之处在于,hinge损失对判定边界附近的点的惩罚力度较高,而感知损失只要样本的类别判定正确即可,而不需要其离判别边界的距离,这样的变化使得其比hinge损失简单,但是泛化能力没有hinge损失强。
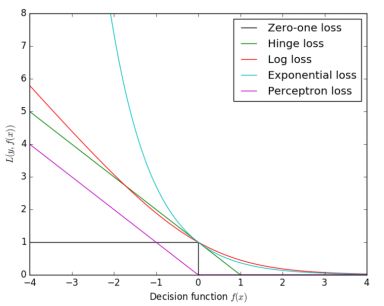
这几种损失函数形式如下,可以看出,除了0-1函数,其他函数都可认为是0-1函数的替代函数,目的在于使函数更平滑,提高计算性,如图所示。
平方(均方)损失函数
具体形式为:
平方损失函数较多应用于回归任务,它假设样本和噪声都是服从高斯分布的,是连续的。它有几个特点:计算简单方便;欧式距离是一种很好的相似度度量标准;在不同的表示域变换后特征性质不变。因此平方损失函数也是一种应用较多的形式。
在TensorFlow中计算平方损失,一般采用tf.pow(x,y),其返回值是x^y。举例来说:
loss = tf.reduce_mean(tf.pow(y-y_, 2))
绝对值损失函数
具体形式为:
绝对值损失函数与平方损失函数类似,不同之处在于平方损失函数更平滑,计算更简便,因此实际应用中更多地使用平方损失函数。
以上主要讲了损失函数的常见形式,在神经网络中应用较多的是对数损失函数(交叉熵)和平方损失函数。可以看出,损失函数的选择与模型是密切相关的,如果是square loss,就是最小二乘了,如果是hinge loss,就是SVM了;如果是exp-loss,那就是boosting了;如果是log loss,那就是logistic regression了,等等。不同的loss函数,具有不同的拟合特性,就需要具体问题具体分析。
自定义损失函数
Tensorflow不仅支持经典的损失函数,还可以优化任意的自定义损失函数。自定义的损失函数原则上满足上文中讲的两个条件即可。TensorFlow提供了很多计算函数,基本可以满足自定义损失函数可能会用到的计算操作。举例来说,预测商品销量时,假设商品成本为1元,销售价为10,如果预测少一个,意味着少挣9元,但预测多一个,意味只损失1元,希望利润最大化,因此损失函数不能采用均方误差,需要自定义损失函数,定义如下:
在TensorFlow中可以这样定义:其中tf.greater()用于比较输入两个张量每个元素的大小,并返回比较结果。Tf.select()会根据第一个输入是否为true,来选择第二个参数,还是第三个参数,类似三目运算符。
loss=tf.reduce_sum(tf.select(tf.greater(v1,v2),a*(v1-v2),b*(v2-v1)))
往期精彩回顾
适合初学者入门人工智能的路线及资料下载机器学习在线手册深度学习在线手册AI基础下载(pdf更新到25集)本站qq群1003271085,加入微信群请回复“加群”获取一折本站知识星球优惠券,复制链接直接打开:https://t.zsxq.com/yFQV7am喜欢文章,点个在看