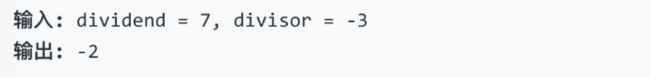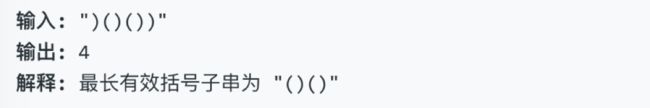LeetCode刷题笔记(Java)---第19-40题
文章目录
- 全部章节
- 1-18题
- 19-40题
- 41-60题
- 61-80题
- 81-100题
- 101-120题
- 121-140题
- 19.删除链表的倒数第N个节点
- 20.有效的括号
- 21.合并两个有序链表
- 22.括号生成
- 23.合并K个排序链表
- 24. 两两交换链表中的节点
- 25. K个一组翻转链表
- 26.删除排序数组中的重复项
- 27. 移除元素
- 28. 实现 strStr()
- 29. 两数相除
- 30. 串联所有单词的子串
- 31. 下一个排列
- 32. 最长有效括号
- 33. 搜索旋转排序数组
- 34. 在排序数组中查找元素的第一个和最后一个位置
- 35. 搜索插入位置
- 36. 有效的数独
- 37. 解数独
- 38. 外观数列
- 39. 组合总和
- 40. 组合总和 II
全部章节
1-18题
19-40题
41-60题
61-80题
81-100题
101-120题
121-140题
19.删除链表的倒数第N个节点
给定一个链表,删除链表的倒数第 n 个节点,并且返回链表的头结点。
示例:

说明:
给定的 n 保证是有效的。
进阶:
你能尝试使用一趟扫描实现吗?
- 解答
class ListNode {
int val;
ListNode next;
ListNode(int x) {
val = x;
}
}
public ListNode removeNthFromEnd(ListNode head, int n) {
ListNode succ = null;
ListNode p = head;
if (n == 1 && head.next == null) return null;
while (p.next != null) {
p = p.next;
if (n == 0) {
succ = succ.next;
} else {
n--;
if (n == 0) succ = head;
}
}
if (succ == null) head = head.next;
else if (succ.next == p) succ.next = null;
else succ.next = succ.next.next;
return head;
}
-
分析
1.一次遍历,那么就要使用两个指针,一个指针用于遍历所有的节点p,一个指针记录要删除的节点的前一个节点succ。因为是单链表记录删除节点的前一个节点更方便操作。
2.如何设置第二个指针是关键。已知要删除倒数第n个节点。所以可以先让第一个指针跑n次,然后第二个指针再前进。 -
过程
首先设置2个指针,succ初始化为null,p初始化指向头节点。
若n等于1,且链表中只有一个节点,返回null。
遍历链表。p不断的后移,n减一,当n等于0的时候,succ指向头节点。再接下来n等于0的时候,succ后移一位。
结束遍历后,p和succ都已经确定。此时再根据不同的情况来删除节点。
情况1:succ==null,这种情况就是要删除的节点刚好是头节点,此时头节点直接后移一位。
情况2:succ的后一位是p,说明要删除的刚好是p指向的节点,succ的后一位置null即可。
情况3:删除的节点既不是头也不是尾,那么就只要将succ的后继指向它后继的后继即可。
20.有效的括号
给定一个只包括 ‘(’,’)’,’{’,’}’,’[’,’]’ 的字符串,判断字符串是否有效。
有效字符串需满足:
左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
注意空字符串可被认为是有效字符串。
- 解答
public boolean isValid(String s) {
Stack<Character> stack = new Stack<>();
char[] chars = s.toCharArray();
for (char aChar : chars) {
if (stack.size() == 0) {
stack.push(aChar);
} else if (match(stack.peek(), aChar)) {
stack.pop();
} else {
stack.push(aChar);
}
}
return stack.size() == 0;
}
private boolean match(char c1, char c2) {
return (c1 == '(' && c2 == ')') || (c1 == '[' && c2 == ']') || (c1 == '{' && c2 == '}');
}
-
分析
1.利用栈来实现,每次入栈判断与栈顶是否匹配,匹配则栈顶出栈,不同则入栈。
2.若完全匹配,则栈是空的。 -
过程
新建一个栈,再将字符串转数组,遍历数组。若栈空则入栈,若栈顶元素与字符已知,则栈顶出站,否则元素入栈。最后返回栈是否为空即可。
21.合并两个有序链表
将两个有序链表合并为一个新的有序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
- 解答
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
ListNode res = new ListNode(0);
ListNode head = res;
while (l1 != null && l2 != null) {
if (l1.val <= l2.val) {
res.next = l1;
res = res.next;
l1 = l1.next;
} else {
res.next = l2;
res = res.next;
l2 = l2.next;
}
}
if (l1 != null) res.next = l1;
else if (l2 != null) res.next = l2;
return head.next;
}
-
分析
1.已知链表是有序的,所以只需要比较两个链表的头的大小,小的先加入到答案的链表中。
2.若有一个链表为空,则另一个链表直接接到答案链表的后面即可。 -
过程
新建一个答案链表,设置头指针head指向答案链表的头结点。
while循环的条件是已知的两个链表当前指针所指的元素不为空,这样才能比较当前所指的两个元素的大小。
小的一个接到答案链表的后面,修改指针后移。
结束while之后判断已知的两个指针所指的节点是否为空,若不为空,则接在答案链表的后面。这里有且只有一个指针指向的节点不为空。
最后返回头指针指向的后一个节点,即是答案。
22.括号生成
给出 n 代表生成括号的对数,请你写出一个函数,使其能够生成所有可能的并且有效的括号组合。
例如,给出 n = 3,生成结果为:

方法1:
开始想到的笨方法暴力解决,不过也通过了。
- 解答
public List<String> generateParenthesis(int n) {
String s = "()";
List<String> list = new ArrayList<>();
if (n == 1) return new ArrayList<String>() {{
add(s);
}};
Set<String> set = new HashSet<String>() {{
add(s);
}};
set = itr(set, n);
list.addAll(set);
return list;
}
public Set<String> itr(Set<String> stringSet, int num) {
Set<String> set = new HashSet<>();
if (num > 1) {
for (String s : stringSet) {
int l = s.length();
for (int i = 0; i < l - 1; i++) {
if (("" + s.charAt(i)).equals("(") && ("" + s.charAt(i + 1)).equals(")")) {
String newString1 = s.substring(0, i) + leftAndRight(s.substring(i, i + 2)) + s.substring(i + 2, l);
String newString2 = s.substring(0, i) + after(s.substring(i, i + 2)) + s.substring(i + 2, l);
set.add(newString1);
set.add(newString2);
}
}
}
if(num>2)
set = itr(set, num - 1);
}
return set;
}
public String leftAndRight(String s) {
return "(" + s + ")";
}
public String after(String s) {
return s + "()";
}
-
分析
1.n对括号的组合是在n-1对括号的组合的情况下扩展的。
2.在已有的一对括号“()”,其扩展方式只有2中。
第一种是在它的左右两边加,即“(())”
第二种是在它的后面加,前后加都是一样的,即“()()”
3.考虑到不能重复,所以用Set集合。 -
过程
当n等于1直接返回“()”,当n大于1,新建Set集合,集合内元素为“()”。调用itr方法,itr是遍历Set集合中的字符串,按照两种情况,分别遍历每一个字符串进行修改得到新的字符串添加到新的Set集合中,递归调用itr直到满足括号对数等于n。
方法2:
看了大神的代码,感觉自己就是个渣渣,思路很巧妙。
- 解答
public List<String> generateParenthesis(int n) {
List<String> res = new ArrayList<String>();
generate(res, "", 0, 0, n);
return res;
}
//count1统计“(”的个数,count2统计“)”的个数
public void generate(List<String> res , String ans, int count1, int count2, int n){
if(count1 > n || count2 > n) return;
if(count1 == n && count2 == n) res.add(ans);
if(count1 >= count2){
String ans1 = new String(ans);
generate(res, ans+"(", count1+1, count2, n);
generate(res, ans1+")", count1, count2+1, n);
}
}
-
分析
1.比较左右括号数量即可
2.在递归的过程中确保字符串中右括号的数量不能大于左括号,不然已经不符合括号对的条件了。 -
过程
调用generate函数,当左括号的数量大于等于右括号的时候,
在这字符串的基础上,分别加“(”与“)”,递归调用generate,修改参数括号的数量。当有一个括号的数量大于n的时候,跳出,返回到上一层。当左右括号数量一致的时候,说明该组合满足条件加入到答案列表中。
23.合并K个排序链表
合并 k 个排序链表,返回合并后的排序链表。请分析和描述算法的复杂度。
- 解答
public ListNode mergeKLists(ListNode[] lists) {
if (lists == null || lists.length == 0) return null;
return merge(lists, 0, lists.length - 1);
}
private ListNode merge(ListNode[] lists, int left, int right) {
if (left == right) return lists[left];
int mid = left + (right - left) / 2;
ListNode l1 = merge(lists, left, mid);
ListNode l2 = merge(lists, mid + 1, right);
return mergeTwoLists(l1, l2);
}
private ListNode mergeTwoLists(ListNode l1, ListNode l2) {
if (l1 == null) return l2;
if (l2 == null) return l1;
if (l1.val < l2.val) {
l1.next = mergeTwoLists(l1.next, l2);
return l1;
} else {
l2.next = mergeTwoLists(l1,l2.next);
return l2;
}
}
-
分析
1.合并多个链表,可以把问题分而治之,简化成合并两个链表,使用之前的方法。
2.问题就在于如何将问题简化。每次选择两个链表合并。
3.使用分治法
分–将问题分解为规模更小的子问题;
治–将这些规模更小的子问题逐个击破;
合–将已解决的子问题合并,最终得出“母”问题的解; -
过程
若链表数组为空,则返回null。
否则调用merge函数。分化问题规模。每次将列表对半分开,递归merge,直到数组只剩下一个链表,则这个链表即为找到规模最小的问题所需的参数。将找到的两个链表调用两个链表合并的算法,即可得到一个新的链表,新链表返回到上一层递归,与下一个链表结合。直到递归调用完成。即可得到答案。
24. 两两交换链表中的节点
给定一个链表,两两交换其中相邻的节点,并返回交换后的链表。
你不能只是单纯的改变节点内部的值,而是需要实际的进行节点交换。
示例:

public ListNode swapPairs(ListNode head) {
ListNode r = new ListNode(0);
ListNode p = r;
ListNode q = head;
if (head == null || head.next == null) return head;
while (head != null){
if(head.next!=null){
p.next = head.next;
q = head;
head = head.next.next;
p.next.next = q;
p = q;
p.next = null;
}else {
p.next = head;
head = head.next;
}
}
return r.next;
}
-
分析
1.此题考的就是指针的操作,需要额外定义两个指针来帮助数字倒转。
2.若已知链表为空或只有一个则直接返回链表。
3.while循环,每次在一小段的范围内,倒转数字,直到head为空。 -
过程
首先定义一个r节点,来接收答案。辅助节点2个,初始化分别指向r节点与head节点。
判断head是否为空或只有一个节点,若满足则返回head。
进入while循环,循环条件是head不为空。若head的后继不为空
则首先将p的后继指向head的后继。q指向head。head后移两位,这里就是每次修改的步长,因为是颠倒两个数字。p的后继的后继指向q。此时就已完成两个数字的倒转。修改p等于q,为了接下来的操作做准备。p的后继设空,此时p是答案链表的最后一个节点。若head的后继为空
则只需要将head节点,连接到p后面即可。修改head指针,避免进入死循环。
25. K个一组翻转链表
给你一个链表,每 k 个节点一组进行翻转,请你返回翻转后的链表。
k 是一个正整数,它的值小于或等于链表的长度。
如果节点总数不是 k 的整数倍,那么请将最后剩余的节点保持原有顺序。
示例:
给你这个链表:1->2->3->4->5
当 k = 2 时,应当返回: 2->1->4->3->5
当 k = 3 时,应当返回: 3->2->1->4->5
说明:
- 你的算法只能使用常数的额外空间。
- 你不能只是单纯的改变节点内部的值,而是需要实际进行节点交换。
public static ListNode reverseKGroup(ListNode head, int k) {
ListNode p = head;
ListNode res = new ListNode(0);
ListNode last = res;
int num = 1;
while (p != null) {
if (p.next != null) {
p = p.next;
num++;
if (num == k) {
ListNode q = p.next;
ListNode h = p;
p.next = null;
reverse(head);
last.next = h;
last = head;
head = q;
p = q;
num = 1;
}else if(p.next == null){
last.next = head;
while (head.next != null) head = head.next;
last = head;
head = null;
}
}else {
last.next = head;
p = p.next;
}
}
res = res.next;
return res;
}
public static void reverse(ListNode head) {
ListNode r = new ListNode(0);
ListNode q = null;
while (head != null) {
r.next = head;
ListNode p = head.next;
head.next = q;
q = head;
head = p;
}
}
-
分析
1.首先需要一个翻转函数reverse,用头插法可以实现翻转。
2.创建一个接收答案的链表结点res。设置指针last,该指针始终指向res的末尾。设置p指针指向head表头。
3.计数器num,用于记录个数。
4.while循环,p指针后移,并计数,计数达到k进行翻转。修改各种指针,即进行连接,和准备下一轮循环。 -
过程
创建p结点指向表头head,创建答案接收结点res,创建last指针指向res,该指针始终指向res的表尾。计数器num设为1;
开始循环。当p不为空的时候,进入循环体。首先判断p的后继是否为空,不为空的话,p后移,计数器加一。
当计数器的值等于k的时候。设q指针等于p的后继,q指向的节点即是下一节循环开始的节点。设置h指针指向p,h所指向的结点倒转之后就是该子链表的第一个结点。用于与答案连接。设p的后继为null,即切断链表,子链表进行倒转。last的后继指向h,完成连接。修改last为head,因为head一开始指向子链表的头部,翻转后即指向表尾。修改head和p为q,即下一节循环开始的节点。重置计数器。
当计数器的值不等于k且p的后继为空时,则将剩余的链表接在last后面。
若p的后继后继为空时,即只有最后一个节点了,直接接在后面即可。
返回答案链表。
26.删除排序数组中的重复项
给定一个排序数组,你需要在 原地 删除重复出现的元素,使得每个元素只出现一次,返回移除后数组的新长度。
不要使用额外的数组空间,你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。
- 解答
public int removeDuplicates(int[] nums) {
int num = 0;
int p = 1;
int l = nums.length;
if(l == 0 )return num;
for (int i = 0; i < l-1; i++) {
if (nums[i] == nums[p]){
p ++;
}else {
num++;
nums[num] = nums[p];
p++;
}
}
return num+1;
}
-
分析
1.不能有额外的数组空间,那就需要在原数组上进行操作。
2.需要一个计数器记录不重复的个数,以及一个指针用来遍历的时候比较前后数字是否一样。 -
过程
首先定义一个num变量用于记录不重复的个数,因为数组下标是从0开始的。所以实际不重复的个数应该是num+1;num初始设为0是为了之后在原数组上进行修改操作方便。
定义变量p=1。用于之后遍历数组的时候与下标i对应的值进行比较。
计算数组的赏读l。若l等于0则返回0;
遍历数组,当nums[i]等于nums[p]时候,p++;寻找不重复的数字。
当找到不重复的数字的时候,num++;此时num下标对应的数字是和前一位重复的,所以此位置可以修改为一个不重复的值,即nums[p]。之后p++。
直到遍历结束 返回num+1。
27. 移除元素
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。
不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并 原地 修改输入数组。
元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
- 解答
public int removeElement(int[] nums, int val) {
int flag = -1;
int num = 0;
int l = nums.length;
if (l == 0) return 0;
for (int i = 0; i < l; i++) {
if(nums[i] == val){
num ++;
if(flag == - 1){
flag = i;
}
}else if(flag != -1){
nums[flag] = nums[i];
flag++;
}
}
return l - num;
}
-
分析
1.需要在原数组上修改,所以要有标示位用于记录数字要移动的位置。
2.遍历数组找到第一个与val相同的位置。即后续的元素要前移。 -
过程
首先定义变量flag 初始化为-1。定义变量num,记录有多少个与val相同的值。计算数组大小l。若l等于0,则返回0。
遍历数组,找到与val相同的值,num++。若找到第一个与val相同的值,则记录下此时的下标。用于后续元素后移。
若nums[i]不等于val且已经找到第一个与val相同的位置。则将其移到flag标记的位置。
最后返回l-num。
28. 实现 strStr()
实现 strStr() 函数。
给定一个 haystack 字符串和一个 needle 字符串,在 haystack 字符串中找出 needle 字符串出现的第一个位置 (从0开始)。如果不存在,则返回 -1。
public int strStr(String haystack, String needle) {
int flag = -1;
if (needle.length() == 0) return 0;
for (int i = 0; i < haystack.length() - needle.length() + 1; i++) {
for (int j = 0; j < needle.length(); j++) {
if (haystack.charAt(i + j) == needle.charAt(j)) {
if (flag == -1) flag = i;
if (j == needle.length()-1) return flag;
} else {
flag = -1;
break;
}
}
}
return flag;
}
-
分析
1.此题可以用KMP算法,不过有点遗忘了,就先用暴力解决了。
2.遍历haystack字符串,从每个字母开始,与needle字符串去匹配。 -
过程
首先定义个变量flag,用于记录完全匹配的第一个字母的位置。
若needle数组为空,则返回0;
遍历haystack字符串,只需要遍历前haystack.length() - needle.length() + 1个字符。
然后与needle字符串去匹配。若相等,则记录下第一个字母匹配的位置。
若完全匹配,则返回flag。
否则flag置为-1.跳出内层循环。
最后返回flag。
29. 两数相除
给定两个整数,被除数 dividend 和除数 divisor。将两数相除,要求不使用乘法、除法和 mod 运算符。
返回被除数 dividend 除以除数 divisor 得到的商。
- 解答
public int divide(int dividend, int divisor) {
if (dividend == 0) {
return 0;
}
if (dividend == Integer.MIN_VALUE && divisor == -1) {
return Integer.MAX_VALUE;
}
boolean negative;
negative = (dividend ^ divisor) <0;
long t = Math.abs((long) dividend);
long d= Math.abs((long) divisor);
int result = 0;
for (int i=31; i>=0;i--) {
if ((t>>i)>=d) {
result+=1<<i;
t-=d<<i;
}
}
return negative ? -result : result;
}
-
分析
1.不能使用乘除法,取余,那么只能使用加减法来做。而除法的含义,也就是被除数可以减去多少个除数。
2.如果使用减法的话效率会很低,所以可以使用移位来做。 -
过程
判断除数是否为0,若为0则返回0.
若被除数是最小的int类型的整数并且除数等于-1,则直接返回int型的最大值。
使用异或操作来计算符号是否相同。记录下来negative
将除数与被除数取绝对值,方便计算。
设置变量result,用于记录答案。
for循环遍历,将被除数先除以2n。不断减小n去试探,当某个n满足dividend/2n>=divisor时,表示已经找到一个足够大的数。然后就讲被除数减去这个足够大的数。将答案result + 2n。表示被除数减去了2n个除数。以此类推。
最后根据negative 返回result。
30. 串联所有单词的子串
给定一个字符串 s 和一些长度相同的单词 words。找出 s 中恰好可以由 words 中所有单词串联形成的子串的起始位置。
注意子串要与 words 中的单词完全匹配,中间不能有其他字符,但不需要考虑 words 中单词串联的顺序。
- 解答
public static List<Integer> findSubstring(String s, String[] words) {
List<Integer> res = new ArrayList<Integer>();
if (words.length == 0) return res;
int wl = words[0].length();
int wc = words.length;
int win = wc * wl;
Map<String,Integer> map1 = new HashMap<String,Integer>();
for (String w:words) {
if (map1.get(w)==null) map1.put(w,0);
map1.put(w, map1.get(w)+1);
}
int[] wordNums = new int[map1.size()];
int i = 0;
for (Integer n:map1.values()) {
wordNums[i] = n;
i++;
}
int[] f=new int[s.length()];
int wn=1;
for(String w:map1.keySet()) {
int index = -2;
while(index != -1) {
if (index == -2) index=-1;
index = s.indexOf(w, index+1);
if (index >=0) f[index] = wn;
}
wn++;
}
int[] wordNumsWin = new int[map1.size()];
for (int j=0;j+win<=s.length();j++) {
while(f[j]==0) {
j++;
if(j+win>s.length()) return res;
}
int k=j;
while(k<j+win) {
if(f[k] != 0) {
wordNumsWin[f[k]-1]++;
if (wordNumsWin[f[k]-1] > wordNums[f[k]-1]) break;
}else break;
k+=wl;
}
if (k==j+win) {
int mm=0;
for (;mm<map1.size();mm++) {
if (wordNumsWin[mm] != wordNums[mm]) break;
}
if (mm==map1.size()) res.add(j);
}
for (int mm=0;mm<map1.size();mm++) wordNumsWin[mm] = 0;
}
return res;
}
-
分析
1.匹配数组words里面的单词长度是一致的。所以如果字符串s中有words中的单词的组合。那子串的长度一定是数组words中单词的数量*单词的长度。
2.可以利用滑动窗口来判断窗口内的是否满足条件
3.首先缓存所有words中的单词在字符串s中出现的下标,便于后面比较。
4.若匹配到一个单词,则窗口的滑动一个单词的长度。可以加快匹配。 -
过程
定义一个链表数组res用于保存匹配的位置。判断若匹配数组words喂空,则返回空链表。计算words中单词的长度与个数。求得滑动窗口的大小。
定义一个HashMap,出现的单词作为key,它出现的次数作为value。
定义一个数组wordNums,按照map中添加的顺序记录单词的次数。
定义一个与字符串s等长的数组f。用于记录字符串s中匹配单词的首字母的位置。
for循环就是遍历map中的key,即遍历words中出现的单词。
若与s中匹配,在数组f中记录下匹配的首字母位置,其值为words中的第几个单词。
定义一个数组wordNumsWin,大小等于不同单词的个数。
根据滑动窗口来遍历之前初始化过的数组f。找到第一个匹配单词的位置。记录下此时的位置k。
在k的位置,以滑动窗口的大小范围内,寻找下一个单词是否匹配。即k加上单词的长度,判断此时f[k]是否为0,0表示没有单词匹配,不为0表示有单词匹配。并将wordNumsWin[f[k]-1]++。记录匹配了单词的数量。若wordNumsWin[f[k]-1]>wordNums[f[k]-1],表示若匹配的单词的数量超过了words数组中该单词的个数,则跳出while循环。
若此时的k等于滑动窗口的末尾,判断此时的wordNumsWin数组是否与wordNums数组一致,若一致则说明满足匹配条件,将j加入到答案链表数组中。若不一致则放弃该轮的结果。将wordNumsWin数组清空。滑动窗口移动一位,继续上述过程。
31. 下一个排列
实现获取下一个排列的函数,算法需要将给定数字序列重新排列成字典序中下一个更大的排列。
如果不存在下一个更大的排列,则将数字重新排列成最小的排列(即升序排列)。
必须原地修改,只允许使用额外常数空间。
以下是一些例子,输入位于左侧列,其相应输出位于右侧列。
1,2,3 → 1,3,2
3,2,1 → 1,2,3
1,1,5 → 1,5,1
- 解答
public static void nextPermutation(int[] nums) {
if (nums == null || nums.length == 1) {
return;
}
// 从后往前找
int i = nums.length - 1;
while (i > 0) {
// 找到一个比后面数字小的
if (nums[i] > nums[i - 1]) {
// 后面数字的最小值
int min = nums[i];
int k = i;
for (int j = i + 1; j < nums.length; j++) {
// 该最小值要比nums[i-1]大,这样才可以交换
if (nums[j] < min && nums[j] > nums[i - 1]) {
min = nums[j];
// 标记最小值的位置,以便交换
k = j;
}
}
swap(nums, i - 1, k);
// 对交换后,i-1之后的数组排序
Arrays.sort(nums, i, nums.length);
break;
}
i--;
}
// 降序数组直接重排
if (i == 0) {
Arrays.sort(nums);
}
}
private static void swap(int[] nums, int i, int k) {
int tmp = nums[i];
nums[i] = nums[k];
nums[k] = tmp;
}
-
分析
1.从后往前找,找到第一个比后一位数字小的数字。该数字与后面的数字中比他大的数字中最小的一个交换。之后后面的数字按照从小到大排序。
2.若原始数组是降序的,则直接重排序。 -
过程
若原始数组的等于0或1,则直接返回。
while循环,从后往前找,找到第一个比后一个数字小的数字。从这一位置开始,在其后面比他大的数字中,挑出最小的那一个与之交换。交换后,i-1之后的数字从小到大排序。
若while结束,i等于0,则说明原数组是降序排序的。找不到一个数字比其后面数字还要小。此时直接将数组重排序即可。从小到大。
32. 最长有效括号
给定一个只包含 ‘(’ 和 ‘)’ 的字符串,找出最长的包含有效括号的子串的长度。
- 解答
public static int longestValidParentheses(String s) {
int left = 0, right = 0, res = 0;
for (char c : s.toCharArray()) {
if (c == '(')
left++;
else
right++;
if (left == right) {
int tmp = 2 * right;
res = res > tmp ? res : tmp;
}
if (right > left)
left = right = 0;
}
if (left > right) {
left = right = 0;
int length = s.length();
for (int i = length - 1; i >= 0; i--) {
char c = s.charAt(i);
if (c == '(')
left++;
else
right++;
if (left == right) {
int tmp = 2 * left;
res = res > tmp ? res : tmp;
}
if (left > right)
left = right = 0;
}
}
return res;
}
-
分析
1.根据左右括号的数量,来判断是否满足括号对。
2.当左右括号数量一致的时候,则说明括号匹配。
3.右括号数量大于左括号数量则说明已经不满足括号对。
4.正序倒序遍历两次,可以避免“(()”输出是0的问题。实际是2。 -
过程
首先定义变量left和right,用来表示左右括号的数量。
定义res,用来记录最长匹配括号对的长度。
正序遍历字符串,记录左右括号的数量。当左右括号相等的时候,记录下此时的长度。当右括号数量大于左括号的数量的时候,则重置变量left和right。
第一遍遍历结束,若left>right.即出现类似的"(()"这种情况。需要倒序遍历。同上一步一样,最后返回res。
33. 搜索旋转排序数组
假设按照升序排序的数组在预先未知的某个点上进行了旋转。
( 例如,数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。
搜索一个给定的目标值,如果数组中存在这个目标值,则返回它的索引,否则返回 -1 。
你可以假设数组中不存在重复的元素。
你的算法时间复杂度必须是 O(log n) 级别。
- 解答
public int search(int[] nums, int target) {
int len = nums.length;
int left = 0, right = len-1;
while(left <= right){
int mid = (left + right) / 2;
if(nums[mid] == target)
return mid;
else if(nums[mid] < nums[right]){
if(nums[mid] < target && target <= nums[right])
left = mid+1;
else
right = mid-1;
}
else{
if(nums[left] <= target && target < nums[mid])
right = mid-1;
else
left = mid+1;
}
}
return -1;
}
-
分析
1.有时间复杂的要求,可以考虑使用二分查找。
2.将数组从中间分成左右两个,根据中间的值与最右边的值可以判断出左右两个数组哪个是有序的。其次根据中间值与目标值可以判断在左右两个数组中去寻找。 -
过程
首先定义两个变量,left和right,初始化为0与数组长度减一。
二分查找使用while循环,判断条件是left小于等于right。
循环体内,首先得到中间位置的下标mid。若mid所指的位置等于target。则直接返回mid。
若nums[mid]< nums[right]:
则说明右边的数组是有序的,可以比较target是否在nums[mid]和nums[right]之间。若满足这个条件,则将left修改为mid+1,否则right修改为mid-1。
同理,若nums[mid] > nums[right]:
则说明左边的数组是有序的,可以比较targte是否在nums[left]和nums[mid]之间。若满足条件,则将right修改为mid-1,否则将right修改为mid+1。
若最后没有找到则返回-1。
34. 在排序数组中查找元素的第一个和最后一个位置
给定一个按照升序排列的整数数组 nums,和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。
你的算法时间复杂度必须是 O(log n) 级别。
如果数组中不存在目标值,返回 [-1, -1]。
示例 1:

示例 2:

- 解答
public static int[] searchRange(int[] nums, int target) {
int len = nums.length;
int left = 0, right = len - 1;
int[] res = new int[]{-1, -1};
int first = search(nums, left, right, target);
if (first != -1) {
res[0] = first;
res[1] = first;
} else return res;
while (search(nums, left, res[0] - 1, target) != -1) res[0] = search(nums, left, res[0] - 1, target);
while (search(nums, res[1] + 1, right, target) != -1) res[1] = search(nums, res[1] + 1, right, target);
return res;
}
public static int search(int[] nums, int left, int right, int target) {
while (left <= right) {
int mid = (left + right) / 2;
if (nums[mid] == target) return mid;
else if (nums[mid]> target) {
right = mid - 1;
} else left = mid + 1;
}
return -1;
}
-
分析
1.使用二分查找,先找到第一个符合目标的数字的位置。
2.找到后,以这个位置为准,在这个位置之前寻找目标数字,在这个位置之后寻找目标数字。这样最后可以找到开始位置和结束的位置。 -
过程
定义长度为2的数组res来存储答案,left变量初始化为0,right遍历初始化为nums长度减一。
首先执行一次二分查找,若找到符合目标的位置,记录下来。若没有则返回{-1,-1}。
利用二分查找循环查找已找到的目标数字的位置之前的数组部分,看是否还有符合目标的数字。
同理查找已找到的符合目标的位置之后的数组部分,是否还有符合目标的数字。
最后返回res。
35. 搜索插入位置
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
你可以假设数组中无重复元素。
- 解答
public int searchInsert(int[] nums, int target) {
int left = 0, right = nums.length - 1;
int mid = 0;
while (left <= right) {
mid = (left + right) / 2;
if (nums[mid] == target) return mid;
else if (nums[mid] > target) {
right = mid - 1;
} else left = mid + 1;
}
if (nums[mid] < target) return mid + 1;
else return mid;
}
-
分析
1.利用二分查找。寻找目标值
2.根据目标值与最后检索的mid所对应的值的大小,返回插入位置。 -
过程
二分查找寻找目标值,若找到则返回坐标。
若没有找到目标值。则判断nums[mid]与target的大小。若target大,则插入位置为mid+1,否则插入位置为mid。
36. 有效的数独
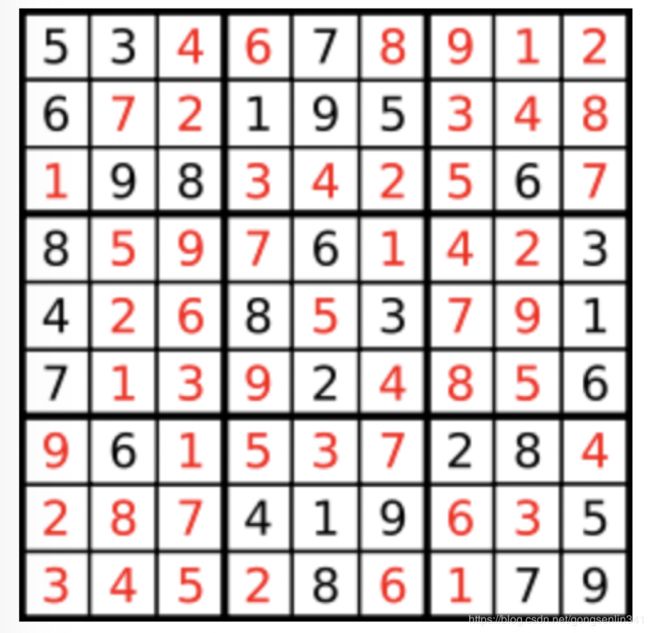
判断一个 9x9 的数独是否有效。只需要根据以下规则,验证已经填入的数字是否有效即可。
1.数字 1-9 在每一行只能出现一次。
2.数字 1-9 在每一列只能出现一次。
3.数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。
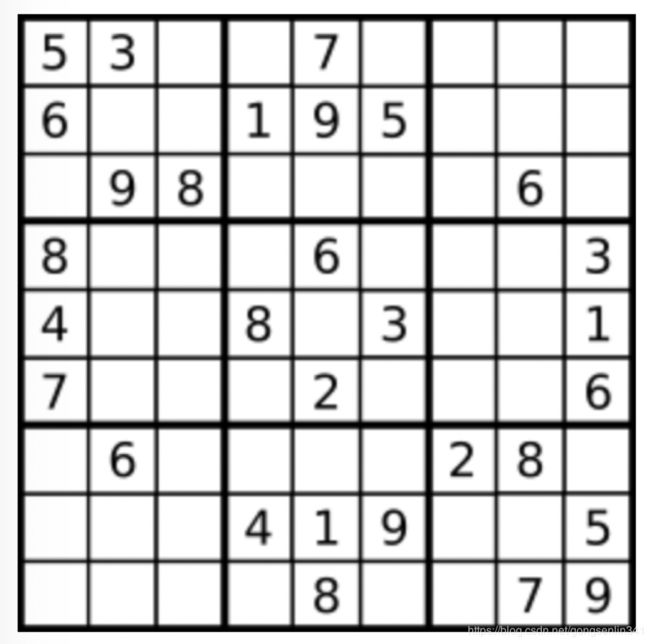
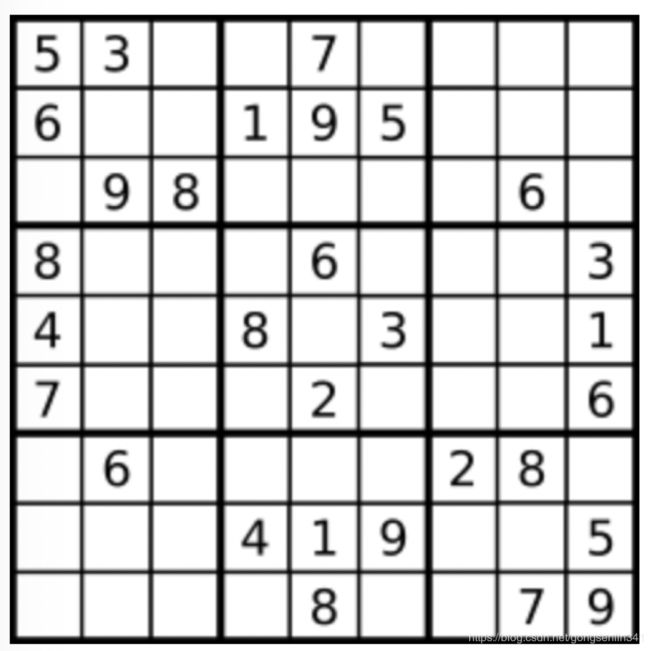
上图是一个部分填充的有效的数独。
数独部分空格内已填入了数字,空白格用 ‘.’ 表示。
说明:
-
一个有效的数独(部分已被填充)不一定是可解的。
-
只需要根据以上规则,验证已经填入的数字是否有效即可。
-
给定数独序列只包含数字 1-9 和字符 ‘.’ 。
-
给定数独永远是 9x9 形式的。
-
解答
public boolean isValidSudoku(char[][] board) {
boolean[][] row = new boolean[9][9];
boolean[][] col = new boolean[9][9];
boolean[][] block = new boolean[9][9];
for (int i = 0; i < 9; i++) {
for (int j = 0; j < 9; j++) {
if (board[i][j] != '.') {
int num = board[i][j] - '1';
int blockIndex = i / 3 + j / 3 * 3;
if (row[i][num] || col[j][num] || block[blockIndex][num]) {
return false;
} else {
row[i][num] = true;
col[j][num] = true;
block[blockIndex][num] = true;
}
}
}
}
return true;
}
-
分析
1.分别三个二维数组来记录已被记录的数字。
2.关于9个33的序号,可以根据i / 3 + j / 3 * 3,来判断是第几个33的格子。 -
过程
定义3个9*9的二维数组
遍历已知的二维数组,将对应的行列中出现的数字,修改三个自定义的二维数组,来记录是否已经出现过。当出现重复的数字,则返回false。
37. 解数独
编写一个程序,通过已填充的空格来解决数独问题。
一个数独的解法需遵循如下规则:
1.数字 1-9 在每一行只能出现一次。
2.数字 1-9 在每一列只能出现一次。
3.数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。
空白格用 ‘.’ 表示。
* 给定的数独序列只包含数字 1-9 和字符 '.' 。
* 你可以假设给定的数独只有唯一解。
* 给定数独永远是 9x9 形式的。
- 解答
public void solveSudoku(char[][] board) {
boolean[][] row = new boolean[9][9];//用于记录每行出现的数字
boolean[][] col = new boolean[9][9];//用于记录每列出现的数字
boolean[][] block = new boolean[9][9];//用于记录每个3*3方格出现的数字
//遍历board,将出现的数字填入对应的三个数组中。
for (int i = 0; i < 9; i++) {
for (int j = 0; j < 9; j++) {
if (board[i][j] != '.') {
int num = board[i][j] - '1';
row[i][num] = true;
col[j][num] = true;
block[i / 3 * 3 + j / 3][num] = true;
}
}
}
dfs(board, row, col, block, 0, 0);
}
private boolean dfs(char[][] board, boolean[][] row, boolean[][] col, boolean[][] block, int i, int j) {
//找到第一个空格为位置。
while (board[i][j] != '.') {
if (++j >= 9) {
i++;
j = 0;
}
if (i >= 9) {
return true;
}
}
//遍历数字1-9,寻找适合填入该空格的数字。
for (int num = 0; num < 9; num++) {
int blockIndex = i / 3 * 3 + j / 3;
if (!row[i][num] && !col[j][num] && !block[blockIndex][num]) {
board[i][j] = (char) ('1' + num);
row[i][num] = true;
col[j][num] = true;
block[blockIndex][num] = true;
//递归调用,继续寻找空格填入数字。
if (dfs(board, row, col, block, i, j)) {
return true;
//若无合适数字,则回溯,将上一个填入的数字擦去。
} else {
row[i][num] = false;
col[j][num] = false;
block[blockIndex][num] = false;
board[i][j] = '.';
}
}
}
return false;
}
-
分析
1.首先用上一题的方法,记录下每行每列每一个3*3的格子里已有的数字。
2.遍历数组寻找空格位置,判断填入的数字,递归调用dfs。若没有合适的填入数字则返回false。返回上一层递归。回溯擦去填入的数字。 -
过程
首先定义3个99的二维数组,用于记录行列和9个33方格内的数字。利用上一题方法,记录下已有的数字。
dfs方法,首先寻找第一个空格,然后遍历1-9的数字,判断哪个数字没有出现在行列货3*3方格中。则将其填入,即修改3个数组对应的位置为true。
递归调用dfs。
若没有找到合适填入的数字。则返回上一层,回溯,将数字擦除,即修改3个数组对应的位置为false。
38. 外观数列
「外观数列」是一个整数序列,从数字 1 开始,序列中的每一项都是对前一项的描述。前五项如下:

1 被读作 “one 1” (“一个一”) , 即 11。
11 被读作 “two 1s” (“两个一”), 即 21。
21 被读作 “one 2”, “one 1” (“一个二” , “一个一”) , 即 1211。
给定一个正整数 n(1 ≤ n ≤ 30),输出外观数列的第 n 项。
注意:整数序列中的每一项将表示为一个字符串。
- 解答
public static String countAndSay(int n) {
String str = "1";//初始化第一个序列
if (n == 1) return str;
StringBuilder stringBuilder = new StringBuilder();
int number = 1;
//遍历n-1次。得到各个序列。
for (int i = 0; i < n - 1; i++) {
//遍历str
for (int j = 0; j < str.length(); j++) {
if (j + 1 < str.length()) {
//若有一样的数字,则记录数量
if (str.charAt(j) == str.charAt(j + 1)) {
number++;
} else {
stringBuilder.append(number).append(str.charAt(j));//若不一样则直接将当前的个数和数字填入新的序列中。重置number
number = 1;
}
} else {
//当只有一个数字,则直接插入11。
if (j == 0) stringBuilder.append(1).append(str.charAt(j));
// str遍历到最后的时候 number不等于1,则将此时的number和数字插入。
else if (number != 1) {
stringBuilder.append(number).append(str.charAt(j));
number = 1;
} else if (str.charAt(j) != str.charAt(j - 1)) stringBuilder.append(1).append(str.charAt(j));//若最后一位与前一位不同,则插入1和该数字。
}
}
//得到新的序列。
str = stringBuilder.toString();
//清楚stringBuilder。
stringBuilder.delete(0, stringBuilder.length());
}
return str;
}
-
分析
1.序列规律是对上一个序列的描述。即前一个是“1”,则下一个序列就是要描述它,1个“1”,所以记为11。同理下一个序列是描述“11”,2个“1”,所以记为21。以此类推。
39. 组合总和
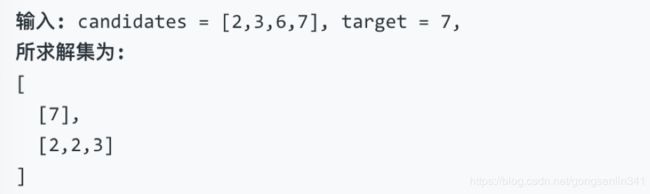
给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的数字可以无限制重复被选取。
说明:
- 所有数字(包括 target)都是正整数。
- 解集不能包含重复的组合。
- 解答
public List<List<Integer>> combinationSum(int[] candidates, int target) {
//用于接收答案
List<List<Integer>> res = new ArrayList<>();
//排序后方便后续的回溯
Arrays.sort(candidates);
//回溯算法。
backtrack(candidates, target, res, 0, new ArrayList<>());
return res;
}
private void backtrack(int[] candidates, int target, List<List<Integer>> res, int i, ArrayList<Integer> tmp_list) {
if (target < 0) return;
//当target == 0,则说明此时找到了符合条件的组合。
if (target == 0) {
res.add(new ArrayList<>(tmp_list));
return;
}
//遍历数组,当前数组值加入链表数组中。递归调用backtrack,此时参数target减去加入链表数组中的那个数,参数i=j,避免有重复的组合。若target小于0,则跳出到上一层递归。链表数组中移除最后一个加进去的值。
for (int j = i; j < candidates.length; j++) {
if (target < 0) break;
tmp_list.add(candidates[j]);
backtrack(candidates, target - candidates[j], res, j, tmp_list);
tmp_list.remove(tmp_list.size() - 1);
}
}
-
分析
1.像这类有一定规律,寻找组合的算法,可以考虑递归+回溯来实现。
2.为了方便最好将数组先排序。
40. 组合总和 II
给定一个数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用一次。
说明:
所有数字(包括目标数)都是正整数。
解集不能包含重复的组合。
示例 1:
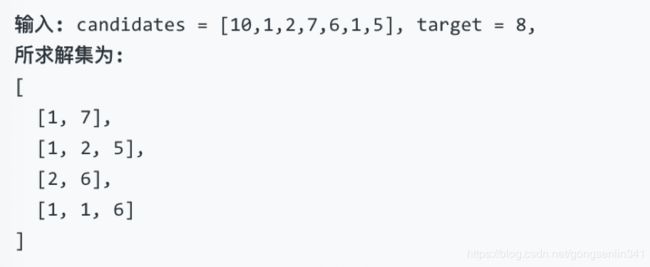
示例 2:
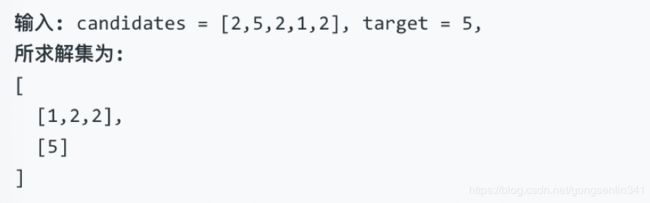
- 解答
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
List<List<Integer>> res = new ArrayList<>();
Arrays.sort(candidates);
backtrack2(candidates, target, res, 0, new ArrayList<>());
return res;
}
private void backtrack2(int[] candidates, int target, List<List<Integer>> res, int i, ArrayList<Integer> tmp_list) {
if (target < 0) return;
if (target == 0) {
res.add(new ArrayList<>(tmp_list));
return;
}
for (int j = i; j < candidates.length; j++) {
//同一层里跳过重复的数。表示不能重复使用。
if(j>i&&candidates[j] == candidates[j-1])continue;
if (target < 0) break;
tmp_list.add(candidates[j]);
backtrack2(candidates, target - candidates[j], res, j + 1, tmp_list);//此处的参数i = j+1,因为不能使用重复数字。
tmp_list.remove(tmp_list.size() - 1);
}
}
-
分析
1.与上一题的不同之处在于数字不能重复使用。if(j>i&&candidates[j] == candidates[j-1])continue;可以跳过重复使用的数字。