LeetCode刷题笔记（Java）---第101-120题
文章目录
- 全部章节
- 1-18题
- 19-40题
- 41-60题
- 61-80题
- 81-100题
- 101-120题
- 121-140题
- 101. 对称二叉树
- 102. 二叉树的层序遍历
- 103. 二叉树的锯齿形层次遍历
- 104. 二叉树的最大深度
- 105. 从前序与中序遍历序列构造二叉树
- 106. 从中序与后序遍历序列构造二叉树
- 107. 二叉树的层次遍历 II
- 108. 将有序数组转换为二叉搜索树
- 109. 有序链表转换二叉搜索树
- 110. 平衡二叉树
- 111. 二叉树的最小深度
- 112. 路径总和
- 113. 路径总和 II
- 114. 二叉树展开为链表
- 115. 不同的子序列
- 116. 填充每个节点的下一个右侧节点指针
- 117. 填充每个节点的下一个右侧节点指针 II
- 118. 杨辉三角
- 119. 杨辉三角 II
- 120. 三角形最小路径和
全部章节
1-18题
19-40题
41-60题
61-80题
81-100题
101-120题
121-140题
101. 对称二叉树
给定一个二叉树，检查它是否是镜像对称的。
例如，二叉树 [1,2,2,3,4,4,3] 是对称的。
但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:
进阶：
你可以运用递归和迭代两种方法解决这个问题吗？
- 解答
public static boolean isSymmetric(TreeNode root) {
if(root == null) return true;
return isSymmetric(root.left, root.right);
}
public static boolean isSymmetric(TreeNode leftTree, TreeNode rightTree) {
if (leftTree == null && rightTree == null) return true;//当前比较的两个结点都为空的时候返回true
if ((leftTree == null && rightTree != null) || (leftTree != null && rightTree == null)) return false;//当其中一个结点为空 另一个结点不为空，则返回false
// 比较左边树的左子树和右边树的右子树
if (isSymmetric(leftTree.left, rightTree.right)) {
// 当前比较的结点数值一样
//递归调用 左边树的右子树和右边树的左子树
if (leftTree.val == rightTree.val) {
return isSymmetric(leftTree.right, rightTree.left);
}
}
return false;
}
-
分析
1.对称的二叉树，若根结点不为空，则左子树和右子树对称的话为对称。
2.如何判断左子树和右子树对称，左子树的左孩子和右子树的右孩子相同，左子树的右孩子和右子树的左孩子相同，则说明左子树和右子树对称。
3.根据2 可以递归实现 -
提交结果
102. 二叉树的层序遍历
给你一个二叉树，请你返回其按 层序遍历 得到的节点值。 （即逐层地，从左到右访问所有节点）。
示例：
二叉树：[3,9,20,null,null,15,7],
返回其层次遍历结果：
- 解答
public static List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> res = new ArrayList<>();
backtrack(root, res, 0);
return res;
}
public static void deep(TreeNode root, List<List<Integer>> res, int depth) {
if (root == null) return;//结点为空则返回上一层递归或结束
if (res.size() <= depth)//若当前小于等于遍历的深度
res.add(new ArrayList<>());//则新建一个List来存放当前层的结点
List<Integer> list = res.get(depth);//获取同一层的集合
list.add(root.val);//存入同一层集合中
deep(root.left, res, depth + 1);//递归遍历左孩子，深度加1
deep(root.right, res, depth + 1);//递归遍历右孩子深度加1
}
-
分析
1.因为这题不是直接读取层次遍历的结果序列，而是将每一层都记录下来。
所以可以使用先序遍历递归的模版方法，再加上当前层的参数，就可以将同一层的结点记录在同一个集合中。
2.注意当res的大小等于层次的时候，就要扩大res的大小，新建一个集合用来存下一层的结点。 -
提交结果
103. 二叉树的锯齿形层次遍历
给定一个二叉树，返回其节点值的锯齿形层次遍历。（即先从左往右，再从右往左进行下一层遍历，以此类推，层与层之间交替进行）。
例如：
给定二叉树 [3,9,20,null,null,15,7],
返回锯齿形层次遍历如下：
- 解答
public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
List<List<Integer>> res = new ArrayList<>();
zigzagLevelOrder(root, res, 0);
return res;
}
public void zigzagLevelOrder(TreeNode root, List<List<Integer>> res, int depth) {
if (root == null) return;
if (res.size() == depth) res.add(new ArrayList<>());
List<Integer> list = res.get(depth);//获得同一层已遍历的链表
if (depth % 2 == 0)//这里定义第一层是0，当偶数层的时候，则从左到右的保存数值
list.add(root.val);
else list.add(0, root.val);//当奇数层的时候，则从右到左保存数值，所以后来的数值要添加在已有的数字的左边。
zigzagLevelOrder(root.left, res, depth + 1);
zigzagLevelOrder(root.right, res, depth + 1);
}
-
分析
1.相比较于上一题，只需要判断当前结点属于的层是要从左到右遍历还是从右到左遍历。即可
2.获取同一层已遍历的数值链表，然后根据层数判断插入的位置
3.list.add(Object object)是在原有的链表后面加入数值
list.add(int index,Object object)可在指定的位置加入数值。这样就可以满足从左遍历还是从右遍历。 -
提交结果
104. 二叉树的最大深度
给定一个二叉树，找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例：
返回它的最大深度 3 。
- 解答
public int maxDepth(TreeNode root) {
return maxDepth(root, 0);
}
public int maxDepth(TreeNode root, int MaxDepth) {
if (root == null) return MaxDepth;
int maxLeft = maxDepth(root.left, MaxDepth + 1);
int maxRight = maxDepth(root.right, MaxDepth + 1);
return maxLeft > maxRight ? maxLeft : maxRight;
}
-
分析
1.判断二叉树的高度，就是判断左右子树的高度，选择高的一个的基础上+1
2.使用递归实现，计算左右子树的高度，返回大的一个。
左右子树的高度就是计算其独自的左右子树的高度。以此来递归。 -
提交结果
105. 从前序与中序遍历序列构造二叉树
根据一棵树的前序遍历与中序遍历构造二叉树。
注意:
你可以假设树中没有重复的元素。
例如，给出
返回如下的二叉树：
- 解答
public static TreeNode buildTree(int[] preorder, int[] inorder) {
if(preorder.length==0||inorder.length==0)return null;
//先序遍历的第一个值作为根
TreeNode root = new TreeNode(preorder[0]);
if (preorder.length == 1) return root;
int rootIndex = 0;
//在中序遍历中寻找这个根的位置，即可确定左子树的结点数量和右子树的结点数量
for (int i = 0; i < inorder.length; i++) {
if (inorder[i] == root.val) {
rootIndex = i;
break;
}
}
int leftLen = rootIndex;
//inorder中，根位置前面的部分作为根的左子树的中序遍历的结果
int[] in1 = Arrays.copyOfRange(inorder, 0, leftLen);
// 根位置后面的部分作为根的右子树的中序遍历的结果
int[] in2 = Arrays.copyOfRange(inorder, leftLen + 1, inorder.length);
// 在preorder中，除去第一个根之外，根据左子树结点的数量，确定左子树的先序遍历结果
int[] pre1 = Arrays.copyOfRange(preorder, 1, 1 + leftLen);
// 余下的部分就是右子树的先序遍历结果
int[] pre2 = Arrays.copyOfRange(preorder, 1 + leftLen, preorder.length);
// 左子树不为空
if (pre1.length > 0)
// 根据左子树的先序遍历和中序遍历构建树
root.left = buildTree(pre1, in1);
// 右子树不为空
if (pre2.length > 0)
// 根据右子树的先序遍历和中序遍历构造树
root.right = buildTree(pre2, in2);
return root;
}
-
分析
1.观察先序遍历和中序遍历的结果可以发现
先序遍历的第一个作为根结点。根据这个根结点可以在中序遍历的序列中 找到其位置。该位置的前面部分的结点就是根结点的左子树结点。该位置的后面的部分的结点就是根结点的右子树结点。
2.确定了左右子树结点的数量 就可以递归的构造出左右子树。 -
提交结果
106. 从中序与后序遍历序列构造二叉树
根据一棵树的中序遍历与后序遍历构造二叉树。
注意:
你可以假设树中没有重复的元素。
例如，给出
返回如下的二叉树：
- 解答
public TreeNode buildTree(int[] inorder, int[] postorder) {
if (postorder.length == 0 || inorder.length == 0) return null;
TreeNode root = new TreeNode(postorder[postorder.length - 1]);//后序遍历的最后一个最为根
if (postorder.length == 1) return root;
int rootIndex = 0;
for (int i = 0; i < inorder.length; i++) {//寻找根在中序遍历中的位置
if (inorder[i] == root.val) {
rootIndex = i;
break;
}
}
int leftLen = rootIndex;
//根据中序遍历中根的位置，可以划分出左子树和右子树的中序遍历和后序遍历
int[] subInorder1 = Arrays.copyOfRange(inorder, 0, leftLen);
int[] subInorder2 = Arrays.copyOfRange(inorder,leftLen+1,inorder.length);
int[] subPostorder1 = Arrays.copyOfRange(postorder,0,leftLen);
int[] subPostorder2 = Arrays.copyOfRange(postorder,leftLen,postorder.length-1);
if(subInorder1.length>0)//若左子树不为空，则递归构造左子树
root.left = buildTree(subInorder1,subPostorder1);
if(subInorder2.length>0)//若右子树不为空，则递归构造右子树
root.right = buildTree(subInorder2,subPostorder2);
return root;
}
-
分析
1.这题和上一题类似，二叉树的中序遍历+二叉树的先/后序遍历可以确定唯一的二叉树。
2.每次都现在先/后序遍历中确定根，然后在中序遍历中寻找根的位置，根据根的位置可以划分出左右子树。
3.这题和上一题在拷贝数组上要花费时间，所以可以另外写一个递归函数，方法参数中可以加上中序遍历和后序遍历的起始和结束的位置。
这样就不用拷贝数组花费额外开销了。过程类似，就不写了 -
提交结果
107. 二叉树的层次遍历 II
给定一个二叉树，返回其节点值自底向上的层次遍历。 （即按从叶子节点所在层到根节点所在的层，逐层从左向右遍历）
例如：
给定二叉树 [3,9,20,null,null,15,7],
返回其自底向上的层次遍历为：
- 解答
public List<List<Integer>> levelOrderBottom(TreeNode root) {
List<List<Integer>> res = new ArrayList<>();
levelOrderBottom(root, res, 0);
return res;
}
public void levelOrderBottom(TreeNode root, List<List<Integer>> res, int depth) {
if (root == null) return;
if (res.size() <= depth) {
res.add(0, new ArrayList<>());//因为是从底向上，所以新的一层需要在原来一层的前面，即在0的位置新建一个集合。
}
List<Integer> list = res.get(res.size() - depth - 1);//原来depth层的元素，因为要从底向上，所以插入的集合位置在res.size() - depth - 1。从下往上数
list.add(root.val);
levelOrderBottom(root.left, res, depth + 1);
levelOrderBottom(root.right, res, depth + 1);
}
-
分析
1.向比较与之前的从上到下的层次遍历，唯一的区别就在于构建新的一层的存储集合，和寻找插入的集合。
2.为了满足从底到上的顺序，所以存储每一层的集合需要在原有的集合链表的前面，即在位置0的地方新建一个该层的用于存储这一层的集合。相当于从下往上数层次。
3.根据结点所在的层次depth，从下往上数，就可找到要插入的集合。即res.size() - depth - 1 就是要插入的集合的下标。 -
提交结果
108. 将有序数组转换为二叉搜索树
将一个按照升序排列的有序数组，转换为一棵高度平衡二叉搜索树。
本题中，一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1。
示例:
- 解答
public static TreeNode sortedArrayToBST(int[] nums) {
TreeNode root = sortedArrayToBST(nums, 0, nums.length - 1);
return root;
}
public static TreeNode sortedArrayToBST(int[] nums, int start, int end) {
if(end < start) return null;
if (start == end) return new TreeNode(nums[start]);
int mid = (end + start + 1) / 2;//数组中间的值作为根，这样可以保证平衡
TreeNode root = new TreeNode(nums[mid]);
// 前一半作为左子树
root.left = sortedArrayToBST(nums, start, mid - 1);
// 后一半作为右子树
root.right = sortedArrayToBST(nums, mid + 1, end);
return root;
}
-
分析
1.数组本身是升序排序的，为了保证高度平衡，所以选择数组中间的值作为根，左边数值均小于中间值，可以作为根的左子树。右边同理。
2.递归生成左右子树。当数组仅有一个数值的时候，这个值直接作为根返回，当参数end小于start的时候直接返回null。 -
提交结果
109. 有序链表转换二叉搜索树
给定一个单链表，其中的元素按升序排序，将其转换为高度平衡的二叉搜索树。
本题中，一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1。
示例:
- 解答
public TreeNode sortedListToBST(ListNode head) {
if(head==null)return null;
if(head.next == null)return new TreeNode(head.val);
ListNode pre = head;
ListNode p = head.next;
ListNode doubleAdd = p.next;
// 找到中间结点p
while (doubleAdd!=null && doubleAdd.next!=null){
pre = p;
p = pre.next;
doubleAdd = doubleAdd.next.next;
}
pre.next = null;// 中间结点前面断开
TreeNode root = new TreeNode(p.val);//中间结点的值作为树的根
root.left = sortedListToBST(head);//前半段作为root的左子树
root.right = sortedListToBST(p.next);//后半段左右root的右子树
return root;
}
-
分析
1.和上一题类似，寻找有序链表中的中间结点作为根，前半段为左子树，后半段为右子树
2.递归构造子树的根结点即可。 -
提交结果
110. 平衡二叉树
给定一个二叉树，判断它是否是高度平衡的二叉树。
本题中，一棵高度平衡二叉树定义为：
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。
示例 1:
给定二叉树 [3,9,20,null,null,15,7]
返回 true 。
示例 2:
给定二叉树 [1,2,2,3,3,null,null,4,4]
返回 false 。
- 解答
public boolean isBalanced(TreeNode root) {
if (root == null) return true;
// 左右子树高度差的绝对值大于1 返回false，说明不平衡
if (Math.abs(getHieght(root.left, 0) - getHieght(root.right, 0)) > 1)
return false;
// 否则 递归判断左子树是否满足平衡 和右子树是否满足平衡
else return isBalanced(root.left) && isBalanced(root.right);
}
// 计算二叉树的高度
public int getHieght(TreeNode root, int height) {
if (root == null) return height;
return Math.max(getHieght(root.left, height + 1), getHieght(root.right, height + 1));
}
-
分析
1.前面有一题就是计算二叉树的高度，此时只需要多一个判断，即判断根结点的左右子树高度之差的绝对值是否大于1。
2.除了根结点满足之外，左右子树的根结点也要满足这一结果。即递归的判断左子树和右子树是否平衡。直到判断到叶子结点为止 -
提交结果
111. 二叉树的最小深度
给定一个二叉树，找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树 [3,9,20,null,null,15,7],
返回它的最小深度 2.
- 解答
public static int minDepth(TreeNode root) {
if (root == null) return 0;
// 返回左右子树中最接近叶子结点的值
if (root.left != null && root.right != null)
return Math.min(minDepth(root.left) + 1, minDepth(root.right) + 1);
else if (root.left == null && root.right == null) return 1;// 找到叶子结点返回1
else if (root.left == null) return minDepth(root.right) + 1;// 左孩子为null 左子树不参与比较，返回右子树的最小深度
else return minDepth(root.left) + 1;// 右孩子为null 返回右子树的最小深度
}
-
分析
1.返回最小深度，就是判断在左右子树的深度上，选择一个小的+1，
2.若没有孩子，则返回1，表示这层深度为1
3.若其中一边的子树为空，则不用比较，直接返回另一边子树的最小深度。
4.一直递归寻找子树的最小深度。 -
提交结果
112. 路径总和
给定一个二叉树和一个目标和，判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和。
说明: 叶子节点是指没有子节点的节点。
示例:
返回 true, 因为存在目标和为 22 的根节点到叶子节点的路径 5->4->11->2。
- 解答
public boolean hasPathSum(TreeNode root, int sum) {
if(root == null) return false;
// 左右子树不为空，则判断左右子树是否有满足条件的路径，sum-root.val
if (root.left != null && root.right != null)
return hasPathSum(root.left, sum - root.val) || hasPathSum(root.right, sum - root.val);
// 右子树为空，则判断左子树是否有满足条件的路径,sum-root.val
else if (root.left != null)
return hasPathSum(root.left, sum - root.val);
// 左子树为空，则判断右子树是否有满足条件的路径,sum-root.val
else if (root.right != null)
return hasPathSum(root.right, sum - root.val);
// 叶子结点，此时只要判断值和sum是否相等即可判断根到该叶子结点的路径满足。
return root.val == sum;
}
-
分析
1.目标值减去当前根结点的值，就是左右子树判断的目标值。
2.一直递归到叶子结点，比较结点值是否和目标值一致即可判断出是否满足条件。 -
提交结果
113. 路径总和 II
给定一个二叉树和一个目标和，找到所有从根节点到叶子节点路径总和等于给定目标和的路径。
说明: 叶子节点是指没有子节点的节点。
示例:
给定如下二叉树，以及目标和 sum = 22，
返回:
- 解答
public List<List<Integer>> pathSum(TreeNode root, int sum) {
List<List<Integer>> res = new ArrayList<>();
if(root==null) return res;
List<Integer> tmp = new ArrayList<>();
tmp.add(root.val);
pathSum(res, tmp, root, sum - root.val);
return res;
}
public void pathSum(List<List<Integer>> res, List<Integer> tmp, TreeNode root, int sum) {
// 当遍历到叶子结点，并且满足路径条件，则将路径加入到答案集合中
if (root.left == null && root.right == null && sum == 0) {
res.add(new ArrayList<>(tmp));
return;
}
// 遍历到叶子结点，但不满足路径条件，则返回上一层递归
else if (root.left == null && root.right == null) {
return;
}
// 回溯法
if (root.left != null) {// 左孩子存在
tmp.add(root.left.val);// 左孩子的值加入到路径组合中
pathSum(res, tmp, root.left, sum - root.left.val);// 递归，判断左孩子
tmp.remove(tmp.size() - 1);// 回溯，去掉刚加入的值
}
// 右孩子同理
if (root.right != null) {
tmp.add(root.right.val);
pathSum(res, tmp, root.right, sum - root.right.val);
tmp.remove(tmp.size() - 1);
}
}
-
分析
1.相比较于上一题，就多了需要将满足条件的组合找出来
2.排列组合的问题，想到用回溯法来做。
3.先左孩子递归，再右孩子递归，直到叶子结点，判断叶子结点时的sum值，保存结果跳出递归。 -
提交结果
114. 二叉树展开为链表
给定一个二叉树，原地将它展开为链表。
例如，给定二叉树
将其展开为：
- 解答
public static void flatten(TreeNode root) {
if(root == null) return;
flatten(root.left);
flatten(root.right);
TreeNode p = root.right;// p指向右子树的头结点
root.right = root.left;// root的右孩子指向左子树
root.left = null;// root的左孩子置空
while(root.right != null) root = root.right;//寻找root的最右的叶子结点
root.right = p;//最右的叶子结点右孩子指向p
}
-
分析
1.从底部向上，将每个结点的左子树移动到右孩子上，原来的右子树，接到原来左子树的最右边的叶子结点上。
2.可以使用后序遍历，先对底下的结点操作，再完成上面的结点。 -
提交结果
115. 不同的子序列
给定一个字符串 S 和一个字符串 T，计算在 S 的子序列中 T 出现的个数。
一个字符串的一个子序列是指，通过删除一些（也可以不删除）字符且不干扰剩余字符相对位置所组成的新字符串。（例如，“ACE” 是 “ABCDE” 的一个子序列，而 “AEC” 不是）
题目数据保证答案符合 32 位带符号整数范围。
示例 1：
示例 2：
- 解答
// 方法一
public static int numDistinct(String s, String t) {
int[][] dp = new int[t.length() + 1][s.length() + 1];
//初始化第一行全为1
for (int i = 0; i <= s.length(); i++) {
dp[0][i] = 1;
}
// 外层循环遍历t
for (int i = 1; i <= t.length(); i++) {
// 内层循环从i开始 遍历s
for (int j = i; j <= s.length(); j++) {
// 当比较的两个字符一致的时候 dp[i][j]满足如下条件
if (s.charAt(j - 1) == t.charAt(i - 1)) {
dp[i][j] = dp[i - 1][j - 1] + dp[i][j - 1];
}
// 否则
else dp[i][j] = dp[i][j - 1];
}
}
return dp[t.length()][s.length()];
}
// 方法二
public static int numDistinct2(String s, String t) {
int[] dp = new int[s.length() + 1];
int pre = 1;
// 改用一维数组
for (int i = 0; i < dp.length; i++) {
dp[i] = 1;
}
for (int i = 1; i <= t.length(); i++) {
for (int j = 0; j <= s.length(); j++) {
int tmp = dp[j]; // 这里的tmp相当于二维数组里的dp[i-1][j-1]
if (j == 0) dp[j] = 0;
else if (s.charAt(j - 1) == t.charAt(i - 1))
dp[j] = dp[j - 1] + pre;//dp[j-1]相当于 二维数组里的dp[i][j-1]
else dp[j] = dp[j - 1];
pre = tmp;
}
}
return dp[s.length()];
}
-
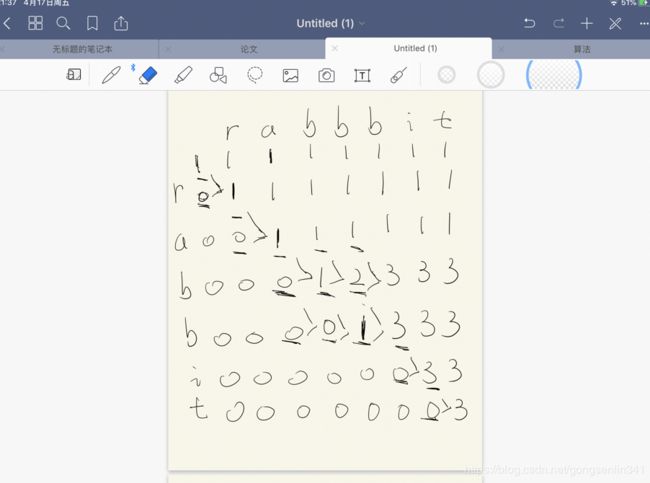
分析
1.方法一，使用动态规划实现，如下图所示：
当两个字符一致的时候
dp[i][j] = dp[i-1][j-1] + dp[i][j-1]
否则
dp[i][j] = dp[i][j-1]
2.方法二是在方法一的基础上改进
使用一维的dp数组，原理一致只是用
用tmp来存放dp[i-1][j-1]
- 提交结果
方法一
方法二
116. 填充每个节点的下一个右侧节点指针
给定一个完美二叉树，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：
填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。
初始状态下，所有 next 指针都被设置为 NULL。
示例：
提示：
- 你只能使用常量级额外空间。
- 使用递归解题也符合要求，本题中递归程序占用的栈空间不算做额外的空间复杂度。
- 解答
public static Node connect(Node root) {
if (root == null) return null;
LinkedList<Node> linkedList = new LinkedList<>();//队列
linkedList.add(root);//根加入队中
int number = -1;// 用于记录结点所在位置
int f = 1;// 和number进行比较即可判断出是否是最右边的结点，初始值为1
Node pre = null;//用来记录前一个结点
while (!linkedList.isEmpty()) {//队不为空
Node p = linkedList.removeFirst();//从队头取出一个结点
number++;// 计数+1
// 当前缀不为空 并且 numer不等于f，则前驱的next指向该结点
if (pre != null && number != f) {
pre.next = p;
}
// 当number 和f一致，说明已找到这一层的最右结点，更新f，来判断下一层的最右结点
else if (number == f)
f = 2 * f + 1;
// p的左右孩子入队
if (p.left != null)
linkedList.add(p.left);
if (p.right != null)
linkedList.add(p.right);
// 记录下p用于和右边兄弟相连
pre = p;
}
return root;
}
-
分析
1.因为是一颗满二叉树，所以最右的结点一定是2的某次方-1.根据这一条件可以用一个计数标志位来记录结点的位置。
2.然后在记录下遍历当前结点的前一个结点。方便连接操作。
3.利用队列来实现层次遍历。 -
提交结果
117. 填充每个节点的下一个右侧节点指针 II
给定一个二叉树
填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。
初始状态下，所有 next 指针都被设置为 NULL。
进阶：
- 你只能使用常量级额外空间。
- 使用递归解题也符合要求，本题中递归程序占用的栈空间不算做额外的空间复杂度。
示例：
- 解答
public static Node connect(Node root) {
if (root == null) return null;
LinkedList<Node> linkedList = new LinkedList<>();
linkedList.add(root);//根结点入队
while (!linkedList.isEmpty()) {
//计算队内大小，即该层所有的结点数量
int size = linkedList.size();
Node pre = null;//记录同一层结点的前一个结点
//遍历这一层结点出队，将这一层结点的下一层结点都入队。
for (int i = 0; i < size; i++) {
Node node = linkedList.removeFirst();
if (i > 0)//连接
pre.next = node;
if(node.left!=null)
linkedList.add(node.left);
if(node.right!=null)
linkedList.add(node.right);
pre = node;//记录当前的结点，用于和后序结点连接
}
}
return root;
}
-
分析
1.层次遍历while里面套个for。每次遍历一层结点
2.记录下当前遍历的结点，用于和后序结点连接 -
提交结果
118. 杨辉三角
给定一个非负整数 numRows，生成杨辉三角的前 numRows 行。
在杨辉三角中，每个数是它左上方和右上方的数的和。
示例:
- 解答
public List<List<Integer>> generate(int numRows) {
List<List<Integer>> res = new ArrayList<>();
if (numRows == 0) return res;
List<Integer> list = new ArrayList<>();
//第一层
list.add(1);
res.add(new ArrayList<>(new ArrayList<>(list)));
// 遍历需要多少层
for (int i = 1; i < numRows; i++) {
//获得上一层的元素链表
list = res.get(res.size() - 1);
//新建该层链表
List<Integer> tmp = new ArrayList<>();
tmp.add(1);//链表头是1
//中间部分，是上面两个数字相加
for (int j = 0; j < list.size() - 1; j++) {
tmp.add(list.get(j) + list.get(j + 1));
}
tmp.add(1);//链表结尾是1
//加入答案集合中
res.add(new ArrayList<>(new ArrayList<>(tmp)));
}
return res;
}
-
分析
1.观察杨辉三角可以发现，第一个和最后一个是1。
2.只需要补齐每一层的中间部分，每一层的中间部分和上一层有关。 -
提交结果
119. 杨辉三角 II
给定一个非负索引 k，其中 k ≤ 33，返回杨辉三角的第 k 行。
在杨辉三角中，每个数是它左上方和右上方的数的和。
示例:
进阶：
你可以优化你的算法到 O(k) 空间复杂度吗？
- 解答
public List<Integer> getRow(int rowIndex) {
List<Integer> pre = new ArrayList<>();//记录前一层
List<Integer> res = new ArrayList<>();//当前层
for (int i = 0; i <= rowIndex; i++) {
res = new ArrayList<>();
for (int j = 0; j <= i; j++) {
//第一个和最后一个为1
if (j == 0 || j == i) {
res.add(1);
}
//中间的为上一层的上面两个数字相加
else {
res.add(pre.get(j - 1) + pre.get(j));
}
}
pre = res;//当前层记录下来
}
return res;
}
public List<Integer> getRow(int rowIndex) {
int pre = 1;
List<Integer> res = new ArrayList<>();
res.add(1);
for (int i = 1; i <= rowIndex; i++) {
for (int j = 1; j < i; j++) {
//记录下当前j位置的值
int temp = res.get(j);
//更新当前的值
res.set(j, pre + res.get(j));
//pre用于更新下一个值
pre = temp;
}
res.add(1);
}
return res;
}
-
分析
1.由于不需要返回整一个杨辉三角，所以只需要记录上一层就可以得到下一层的数值 2.改进，因为每一个值的更新，之和当前这一位置的值和前一位置的值有关。所以只需要把当前欠一个位置之前的值保存起来，用于更新即可。 -
提交结果
改进：
120. 三角形最小路径和
给定一个三角形，找出自顶向下的最小路径和。每一步只能移动到下一行中相邻的结点上。
例如，给定三角形：
自顶向下的最小路径和为 11（即，2 + 3 + 5 + 1 = 11）。
说明：
如果你可以只使用 O(n) 的额外空间（n 为三角形的总行数）来解决这个问题，那么你的算法会很加分。
- 解答
//方法一
public int minimumTotal(List<List<Integer>> triangle) {
// 从倒数第二层开始遍历
for (int i = triangle.size() - 2; i >= 0; i--) {
//第i层结点
List<Integer> list = triangle.get(i);
//第i+1层结点
List<Integer> list2 = triangle.get(i + 1);
//更新第i层结点的值 表示第i层到最底层的最短路径
for (int j = 0; j < triangle.get(i).size(); j++) {
list.set(j, list.get(j) + Math.min(list2.get(j), list2.get(j + 1)));
}
}
//返回最顶层就是最短路径
return triangle.get(0).get(0);
}
-
分析
1.从最底层向上更新每一层到最底层的最短路径。
2.每一层每个结点的最短路径，和他下面一层的相邻两个结点有关，更新选择最小的那一个加上本身，就是这一个结点到底层的最短路径。 -
提交结果
