LeetCode刷题笔记（Java）---第121-140题
文章目录
- 全部章节
- 1-18题
- 19-40题
- 41-60题
- 61-80题
- 81-100题
- 101-120题
- 121-140题
- 121. 买卖股票的最佳时机
- 122. 买卖股票的最佳时机 II
- 123. 买卖股票的最佳时机 III
- 124. 二叉树中的最大路径和
- 125. 验证回文串
- 126. 单词接龙 II
- 127. 单词接龙
- 128. 最长连续序列
- 129. 求根到叶子节点数字之和
- 130. 被围绕的区域
- 131. 分割回文串
- 132. 分割回文串 II
- 133. 克隆图
- 134. 加油站
- 135. 分发糖果
- 136. 只出现一次的数字
- 137. 只出现一次的数字 II
- 138. 复制带随机指针的链表
- 139. 单词拆分
- 140. 单词拆分 II
全部章节
1-18题
19-40题
41-60题
61-80题
81-100题
101-120题
121-140题
121. 买卖股票的最佳时机
给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。
如果你最多只允许完成一笔交易（即买入和卖出一支股票一次），设计一个算法来计算你所能获取的最大利润。
注意：你不能在买入股票前卖出股票。
示例 1:
- 解答
public int maxProfit(int[] prices) {
if (prices.length <= 1) return 0;
int res = 0, min = prices[0];
for (int i = 1; i < prices.length; i++) {
// 记录当前最大收益
res = Math.max(res, prices[i] - min);
// 更新最小值，即买入点
min = Math.min(min, prices[i]);
}
return res;
}
-
分析
1.首先取第一天为最小值，即买入点
2.从第二天开始遍历
计算当天卖出可获得收益，与已知的最大收益做比较
更新最小值，即当天的价格和已知最小价格比较，若当天价格小，则更新最小值，即这天为最佳买入点。
3.最后返回最大收益res即可。 -
提交结果
122. 买卖股票的最佳时机 II
给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易（多次买卖一支股票）。
注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。
示例 1:
示例 2:
示例 3:
- 解答
public int maxProfit2(int[] prices) {
int res = 0;
int price = prices[0];//记录前一天的价格
//从第二天开始遍历
for (int i = 1; i < prices.length; i++) {
//若当天价格比前一天价格高，则记录收益，并更新前一天的价格为当天价格
if(prices[i]>price) {
res += prices[i] - price;
price = prices[i];
}
//否则，仅更新前一天的价格为当天价格，相当于在前一天的时候卖出。不过之前就已经记录了收益，这里就不用记录了。
else price = prices[i];
}
return res;//最后返回收益即可
}
-
分析
1.观察数组可以发现，累计收益最大，就是在递增的子序列的最低处卖出最高处卖出。多个递增子序列就进行多次买卖。
2.所以只需要遍历一次，比较当天价格和前一天的价格是否是递增的，是的话就记录收益，不是的话，说明前一天已经到达峰值，此时仅更新前一天的价格为当天价格即可。 -
提交结果
123. 买卖股票的最佳时机 III
给定一个数组，它的第 i 个元素是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。
注意: 你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。
示例 1:
- 解答
//方法一
public int maxProfit(int[] prices) {
int res = 0;
if (prices.length <= 1) return res;
//划分左右区间，计算最大收益
for (int i = 0; i < prices.length; i++) {
res = Math.max(res, maxProfit(prices, 0, i) + maxProfit(prices, i, prices.length));
}
return res;
}
//计算最大收益
public int maxProfit(int[] prices, int start, int end) {
int res = 0, min = prices[start];
for (int i = start; i < end; i++) {
res = Math.max(res,prices[i]-min);
min = Math.min(min,prices[i]);
}
return res;
}
// 方法二 大神的代码。
public int maxProfit(int[] prices) {
/**
对于任意一天考虑四个变量:
fstBuy: 在该天第一次买入股票可获得的最大收益
fstSell: 在该天第一次卖出股票可获得的最大收益
secBuy: 在该天第二次买入股票可获得的最大收益
secSell: 在该天第二次卖出股票可获得的最大收益
分别对四个变量进行相应的更新, 最后secSell就是最大
收益值(secSell >= fstSell)
**/
int fstBuy = Integer.MIN_VALUE, fstSell = 0;
int secBuy = Integer.MIN_VALUE, secSell = 0;
for(int p : prices) {
fstBuy = Math.max(fstBuy, -p);
fstSell = Math.max(fstSell, fstBuy + p);
secBuy = Math.max(secBuy, fstSell - p);
secSell = Math.max(secSell, secBuy + p);
}
return secSell;
}
-
分析
1.方法一是在120题的基础上的扩展，划分区间，计算各区间最大收益，求和得总体收益。再于已知总体最大收益比较。即可得到出结果。
2.方法二大神代码，记录了4种状态下的最大收益，第一次买卖，第二次买卖。 -
提交结果
方法一
方法二
124. 二叉树中的最大路径和
给定一个非空二叉树，返回其最大路径和。
本题中，路径被定义为一条从树中任意节点出发，达到任意节点的序列。该路径至少包含一个节点，且不一定经过根节点。
示例 1:
示例 2:
- 解答
private int max = Integer.MIN_VALUE;
public int maxPathSum(TreeNode root) {
max(root);
return max;
}
//后序遍历
public int max(TreeNode root) {
if (root == null) return 0;
int maxLeft = Math.max(max(root.left), 0);//左子树的最大路径
int maxRight = Math.max(max(root.right), 0);//右子树的最大路径
max = Math.max(max, maxLeft + root.val + maxRight);//比较root为转折点的最大路径和已知最大路径的值
return root.val + Math.max(maxLeft, maxRight);//root作为路径中的结点，左右子树选择路径之和大的作为路径分支。
}
-
分析
1.后序遍历，先遍历到叶子结点，再逐层往上。计算左右子树的最大路径。
2.判断root作为转折点时候的路径长度等于maxLeft+root.val+maxRight。比较此时的最大值，保留大的
3.返回root作为路径中结点，左右子树的最大路径选择其一作为路径的一部分，给上一层递归。 -
提交结果
125. 验证回文串
给定一个字符串，验证它是否是回文串，只考虑字母和数字字符，可以忽略字母的大小写。
说明：本题中，我们将空字符串定义为有效的回文串。
示例 1:
示例 2:
- 解答
public static boolean isPalindrome(String s) {
s = s.toLowerCase();
int left = 0;//从左遍历
int right = s.length() - 1;//从右遍历
while (left < right) {
//从左遍历到数字或字母
while (left < s.length() && (s.charAt(left) < 48 || (s.charAt(left) > 57 && s.charAt(left) < 65) || (s.charAt(left) > 90 && s.charAt(left) < 97)))
left++;
//从右遍历到数字或字母
while (right > 0 && (s.charAt(right) < 48 || (s.charAt(right) > 57 && s.charAt(right) < 65) || (s.charAt(right) > 90 && s.charAt(right) < 97)))
right--;
//比较，若不相等则返回false
if (left < right && s.charAt(left) != s.charAt(right)) return false;
else {
left++;
right--;
}
}
return true;
}
-
分析
1.设置两个指针，指向开头和结尾，分别遍历到数字或字母然后进行比较。
-
提交结果
126. 单词接龙 II
给定两个单词（beginWord 和 endWord）和一个字典 wordList，找出所有从 beginWord 到 endWord 的最短转换序列。转换需遵循如下规则：
1.每次转换只能改变一个字母。
2.转换过程中的中间单词必须是字典中的单词。
说明:
- 如果不存在这样的转换序列，返回一个空列表。
- 所有单词具有相同的长度。
- 所有单词只由小写字母组成。
- 字典中不存在重复的单词。
- 你可以假设 beginWord 和 endWord 是非空的，且 二者不相同。
示例 1:
示例 2:
- 解答
public static List<List<String>> findLadders(String beginWord, String endWord, List<String> wordList) {
List<List<String>> ans = new ArrayList<>();
// 如果不含有结束单词，直接结束
if (!wordList.contains(endWord)) {
return ans;
}
bfs(beginWord, endWord, wordList, ans);
return ans;
}
public static void bfs(String beginWord, String endWord, List<String> wordList, List<List<String>> ans) {
Queue<List<String>> queue = new LinkedList<>();
List<String> path = new ArrayList<>();
path.add(beginWord);
queue.offer(path);
boolean isFound = false;
Set<String> dict = new HashSet<>(wordList);//转成set集合加快读取
Set<String> visited = new HashSet<>();//使用过的词放入visited中
visited.add(beginWord);
while (!queue.isEmpty()) {//bfs
int size = queue.size();//已找到的序列的个数
Set<String> subVisited = new HashSet<>();
//分别遍历每一个序列
for (int j = 0; j < size; j++) {
List<String> p = queue.poll();//获取第j个序列
//得到当前路径的末尾单词
String temp = p.get(p.size() - 1);//获得队尾元素，也就是上一次找到的单词
// 一次性得到所有的下一个的节点
ArrayList<String> neighbors = getNeighbors(temp, dict);//得到temp的可能变换的情况
for (String neighbor : neighbors) {//遍历所有找到的变换情况
//只考虑之前没有出现过的单词
if (!visited.contains(neighbor)) {
//到达结束单词
if (neighbor.equals(endWord)) {
isFound = true;//退出标志
p.add(neighbor);//序列中加入这个单词
ans.add(new ArrayList<>(p));//答案集合中加入这个序列集合
p.remove(p.size() - 1);//回溯
}
//加入当前单词
p.add(neighbor);
queue.offer(new ArrayList<>(p));//单词序列集合中加入p
p.remove(p.size() - 1);//回溯
subVisited.add(neighbor);//加入到访问过的集合
}
}
}
visited.addAll(subVisited);//设为访问过
if (isFound) {//退出
break;
}
}
}
//找到单词node 可能变化的情况。并且在dict中出现过。
private static ArrayList<String> getNeighbors(String node, Set<String> dict) {
ArrayList<String> res = new ArrayList<String>();
char chs[] = node.toCharArray();
for (char ch = 'a'; ch <= 'z'; ch++) {
for (int i = 0; i < chs.length; i++) {
if (chs[i] == ch)
continue;
char old_ch = chs[i];
chs[i] = ch;
if (dict.contains(String.valueOf(chs))) {
res.add(String.valueOf(chs));
}
chs[i] = old_ch;
}
}
return res;
}
-
分析
1.广度优先遍历。
2.首先beginWord作为根，作为一个找到的子序列，加入到序列队列中。
3.遍历序列队列。
4.获得序列中最后一个单词，即刚加入序列的单词，计算获得存在WordList中所有可能的变换的情况。
5.遍历这些变换的情况，若没有访问过，则序列中加入该单词，得到的新的序列加入到序列队列中。
6.回溯，遍历完所有可能的变换情况后，即可得到这一轮找到的所有子序列。
7.跳到步骤3，直到找到的子序列最后一个单词符合endWord，将找到的序列加入答案集合中，并设置退出标识位为true，退出循环。 -
提交结果
127. 单词接龙
给定两个单词（beginWord 和 endWord）和一个字典，找到从 beginWord 到 endWord 的最短转换序列的长度。转换需遵循如下规则：
1.每次转换只能改变一个字母。
2.转换过程中的中间单词必须是字典中的单词。
说明:
- 如果不存在这样的转换序列，返回 0。
- 所有单词具有相同的长度。
- 所有单词只由小写字母组成。
- 字典中不存在重复的单词。
- 你可以假设 beginWord 和 endWord 是非空的，且二者不相同。
示例 1:
示例 2:
- 解答
public static int ladderLength(String beginWord, String endWord, List<String> wordList) {
if (!wordList.contains(endWord)) return 0;
return bfs(beginWord, endWord, wordList);
}
public static int bfs(String beginWord, String endWord, List<String> wordList) {
Queue<List<String>> queue = new LinkedList<>();//用于存储已找到的序列
List<String> path = new ArrayList<>();//创建第一个序列
path.add(beginWord);//beginWord添加进去
queue.offer(path);//添加到序列集合中
Set<String> dict = new HashSet<>(wordList);//转Set方便读取
Set<String> visited = new HashSet<>();//用于判断是否已经使用过
visited.add(beginWord);//beginWord添加进去
//序列集合不为空
while (!queue.isEmpty()) {
int size = queue.size();//一共多少个序列
Set<String> subVisited = new HashSet<>();
//遍历每一个序列
for (int i = 0; i < size; i++) {
//取出单词序列
List<String> p = queue.poll();
//获得序列中最后一个单词
String last = p.get(p.size() - 1);
//获得这个单词可能的变换情况
ArrayList<String> neighbors = getNeighbors(last, dict);
//遍历上面找到的所有情况
for (String neighbor : neighbors) {
//判断是否已经使用
if (!visited.contains(neighbor)) {
//若找到最后一个单词，则直接返回序列长度
if (neighbor.equals(endWord)) {
return p.size() + 1;
}
//否则加入到序列中
p.add(neighbor);
//新的序列加入到序列集合中
queue.offer(new ArrayList<>(p));
//回溯
p.remove(p.size() - 1);
subVisited.add(neighbor);
}
}
}
visited.addAll(subVisited);
}
return 0;
}
private static ArrayList<String> getNeighbors(String node, Set<String> dict) {
ArrayList<String> res = new ArrayList<String>();
char chs[] = node.toCharArray();
for (char ch = 'a'; ch <= 'z'; ch++) {
for (int i = 0; i < chs.length; i++) {
if (chs[i] == ch)
continue;
char old_ch = chs[i];
chs[i] = ch;
if (dict.contains(String.valueOf(chs))) {
res.add(String.valueOf(chs));
}
chs[i] = old_ch;
}
}
return res;
}
-
分析
1.上一题的简单版，只需要返回最小序列长度即可。
2.方法和上一题类似。 -
提交结果
128. 最长连续序列
给定一个未排序的整数数组，找出最长连续序列的长度。
要求算法的时间复杂度为 O(n)。
示例:
- 解答
public int longestConsecutive(int[] nums) {
Set<Integer> numSet = new HashSet<>();//将数组转成HashSet，方便查找
for (int num : nums) {
numSet.add(num);
}
int longest = 0;//记录最长连续序列长度
//遍历每一个数字。
for (int num : nums) {
//若当前数字有比他小一的存在，则说明这个数字被包括在比他小一的连续序列中不用考虑。
//若没有比它小一的数字存在，则它就是序列的头
if (!numSet.contains(num - 1)) {
int number = num;//记录下序列的头，即序列第一个数字
int len = 1;//初始化长度为1
//while循环，若连续数值存在，则更新number和长度。
while (numSet.contains(number + 1)) {
number += 1;
len++;
}
//判断找到的连续序列和已知的最长序列哪个更长，保留长的。
longest = Math.max(longest, len);
}
}
return longest;
}
-
分析
1.使用HashSet，查找的时间复杂度降到O(1)
2.遍历数值，选择不存在比它小一的数值的数字作为序列的头
3.while判断连续数字是否存在，构成连续序列。
4.保留最大的连续序列返回。 -
提交结果
129. 求根到叶子节点数字之和
给定一个二叉树，它的每个结点都存放一个 0-9 的数字，每条从根到叶子节点的路径都代表一个数字。
例如，从根到叶子节点路径 1->2->3 代表数字 123。
计算从根到叶子节点生成的所有数字之和。
说明: 叶子节点是指没有子节点的节点。
示例 1:
示例 2:
- 解答
private int ans = 0;
public int sumNumbers(TreeNode root) {
sumNumbers(0, root);
return ans;
}
public void sumNumbers(int tmp, TreeNode root) {
if (root == null) return;
tmp = tmp * 10 + root.val;//新数字皆在后面
//找到叶子结点
if (root.left == null && root.right == null) {
ans += tmp;//将tmp加入答案中
return;
}
sumNumbers(tmp, root.left);//递归左孩子
sumNumbers(tmp, root.right);//递归右孩子
}
-
分析
1.先序遍历二叉树，将途径的数字组合起来 2.遇到叶子结点的时候，将得到的数字加入答案中 -
提交结果
130. 被围绕的区域
给定一个二维的矩阵，包含 ‘X’ 和 ‘O’（字母 O）。
找到所有被 ‘X’ 围绕的区域，并将这些区域里所有的 ‘O’ 用 ‘X’ 填充。
示例:
运行你的函数后，矩阵变为：
解释:
被围绕的区间不会存在于边界上，换句话说，任何边界上的 ‘O’ 都不会被填充为 ‘X’。 任何不在边界上，或不与边界上的 ‘O’ 相连的 ‘O’ 最终都会被填充为 ‘X’。如果两个元素在水平或垂直方向相邻，则称它们是“相连”的。
- 解答
static int[] row = new int[]{1, -1, 0, 0};
static int[] column = new int[]{0, 0, 1, -1};
public static void solve(char[][] board) {
if (board == null || board.length == 0 || board[0] == null || board[0].length == 0) return;
int r = board.length;
int c = board[0].length;
for (int i = 0; i < r; i++) {
if (board[i][0] == 'O') dfs(board, i, 0);//第一列边界
if (board[i][c - 1] == 'O') dfs(board, i, c - 1);//最后一列边界
}
for (int i = 0; i < c; i++) {
if (board[0][i] == 'O') dfs(board, 0, i);//第一行边界
if (board[r - 1][i] == 'O') dfs(board, r - 1, i);//最后一行边界
}
//修改
for (int i = 0; i < r; i++) {
for (int j = 0; j < c; j++) {
if (board[i][j] == 'O') board[i][j] = 'X';
if (board[i][j] == 'D') board[i][j] = 'O';
}
}
}
public static void dfs(char[][] board, int r, int c) {
board[r][c] = 'D';
//深度优先搜索
//遍历4个方向，找到相邻的字符'O'，递归，将其改为D，记录下来。D表示不能转换成X
for (int i = 0; i < row.length; i++) {
int r_tmp = r + row[i];
int c_tmp = c + column[i];
if (r_tmp < 0 || r_tmp >= board.length || c_tmp < 0 || c_tmp >= board[0].length || board[r_tmp][c_tmp] != 'O') continue;
dfs(board, r_tmp, c_tmp);
}
}
-
分析
1.遍历数组的行列边界
2.找到行列边界为’O’的点，将这点改为D，深度搜索遍历找到相连接的所有’O’点，将其改为D，表示这些点不被包围。
3.遍历数组，剩下的O就是被X包围的，将其改为X，
刚才标记的D改为原来的O即可。 -
提交结果
131. 分割回文串
给定一个字符串 s，将 s 分割成一些子串，使每个子串都是回文串。
返回 s 所有可能的分割方案。
示例:
- 解答
public List<List<String>> partition(String s) {
char[] chars = s.toCharArray();
List<List<String>> res = new ArrayList<>();
partition(s, res, 0, s.length(), new ArrayList<>());
return res;
}
public void partition(String s, List<List<String>> res, int start, int end, List<String> tmp) {
//不可分割了，tmp加入到res中
if (start == end) {
res.add(new ArrayList<>(tmp));
return;
}
for (int i = start; i < end; i++) {
//从start位置开始寻找回文序列
if (!checkPalindrome(s, start, i)) continue;
tmp.add(s.substring(start, i + 1));//找到的回文序列，加入到tmp中
partition(s, res, i + 1, end, tmp);//递归余下的部分寻找。
tmp.remove(tmp.size() - 1);//回溯
}
}
//判断start开始end结束的序列是否回文
public boolean checkPalindrome(String s, int start, int end) {
while (start < end) {
if (s.charAt(start) != s.charAt(end))
return false;
start++;
end--;
}
return true;
}
-
分析
1.寻找分割点，判断分割出的是否是回文字符串
2.如果是回文，则将其加入到组合中，继续分割余下的部分
3.回溯，去掉已找到的部分，寻找其他可能的分割情况。 -
提交结果
132. 分割回文串 II
给定一个字符串 s，将 s 分割成一些子串，使每个子串都是回文串。
返回符合要求的最少分割次数。
示例:
- 解答
public int minCut(String s) {
int len = s.length();
if (len < 2) {//字符串长度小于2 不用分割
return 0;
}
//dp[i]表示字符串从位置0到位置i最少的分割次数
int[] dp = new int[len];
//初始化为最多的分割次数，n个字符就分割n-1次
for (int i = 0; i < len; i++) {
dp[i] = i;
}
//判断是否是回文的数组
boolean[][] checkPalindrome = new boolean[len][len];
for (int right = 0; right < len; right++) {
for (int left = 0; left <= right; left++) {
if (s.charAt(left) == s.charAt(right) && (right - left <= 2 || checkPalindrome[left + 1][right - 1])) {
checkPalindrome[left][right] = true;
}
}
}
for (int i = 1; i < len; i++) {
//从0-i是一个回文，所有不用分割dp[i]=0
if (checkPalindrome[0][i]){
dp[i] = 0;
continue;
}
//若 0-i不是回文，则需要分割，则遍历0-i，寻找分割点
//判断出最小分割次数
for (int j = 0; j < i; j++) {
//j为分割点 j+1到i是回文，则比较已知的分割次数，和dp[j]出分割次数+1 哪个小。保留小的那个作为0-i的最小分割次数。
if (checkPalindrome[j + 1][i]) {
dp[i] = Math.min(dp[i], dp[j] + 1);
}
}
}
return dp[len - 1];
}
-
分析
1.利用动态规划来实现，dp[i]记录0-i字符串最小分割次数
2.初始化将字符串，一个一个字符都分开，那么dp[i]就等于i。
3.使用数组的方式初始化所有回文，之后查找的时间复杂度就是O(1)。
4.从第二个字符开始遍历，更新0-i的最小分割次数
5.若0-i是回文，那么不需要分割，则dp[i]就等于0
6.若0-i不是回文，则需要分割，那么就要判断分割点
遍历0-i的位置。选择分割点更新dp[i]
若j为分割点，则dp[i] = Math.min(dp[i], dp[j] + 1)
7.最后返回dp[len - 1]。即是字符串最小的分割次数 -
提交结果
133. 克隆图
给你无向 连通 图中一个节点的引用，请你返回该图的 深拷贝（克隆）。
图中的每个节点都包含它的值 val（int） 和其邻居的列表（list[Node]）。
class Node {
public int val;
public List<Node> neighbors;
}
测试用例格式：
简单起见，每个节点的值都和它的索引相同。例如，第一个节点值为 1（val = 1），第二个节点值为 2（val = 2），以此类推。该图在测试用例中使用邻接列表表示。
邻接列表 是用于表示有限图的无序列表的集合。每个列表都描述了图中节点的邻居集。
给定节点将始终是图中的第一个节点（值为 1）。你必须将 给定节点的拷贝 作为对克隆图的引用返回。
示例 1：
示例 2：
示例 3：
示例 4：
- 解答
private HashMap<Node, Node> visited = new HashMap<>();//用于保存拷贝的结点
public Node cloneGraph(Node node) {
if (node == null) {
return node;
}
if (visited.containsKey(node)) {//若已经拷贝过该结点，则直接返回该结点的拷贝
return visited.get(node);
}
Node cloneNode = new Node(node.val, new ArrayList());//拷贝node结点，邻居初始化为空
visited.put(node, cloneNode);
for (Node neighbor : node.neighbors) {//遍历邻居，将邻居添加到新创建对象的邻居中，并递归的创建邻居结点的拷贝。
cloneNode.neighbors.add(cloneGraph(neighbor));
}
return cloneNode;
}
-
分析
1.深度搜索遍历
2.拷贝结点，并初始化邻居为空，遍历原邻居添加到拷贝结点的邻居中。
3.递归的拷贝邻居结点。
4.最后visited保存了所有拷贝的结点，便会结束递归。 -
提交结果
134. 加油站
在一条环路上有 N 个加油站，其中第 i 个加油站有汽油 gas[i] 升。
你有一辆油箱容量无限的的汽车，从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发，开始时油箱为空。
如果你可以绕环路行驶一周，则返回出发时加油站的编号，否则返回 -1。
说明:
- 如果题目有解，该答案即为唯一答案。
- 输入数组均为非空数组，且长度相同。
- 输入数组中的元素均为非负数。
示例 1:
示例 2:
- 解答
public static int canCompleteCircuit(int[] gas, int[] cost) {
int remain = 0;
int len = gas.length;
int index = -1;
for (int i = 0; i < len; i++) {
if (gas[i] < cost[i]) continue;//起始点油不够开往下一个地方，跳过
index = i;//记录起始点
remain = 0;//初始化油为0L
for (int j = 0; j < len; j++) {
remain += gas[(i + j) % len];//加油
remain -= cost[(i + j) % len];//开往下一站
if (remain < 0) {//若小于0说明开不到下一站
index = -1;//清空记录点
break;
}
}
if (index != -1) break;//若找到可以开一圈的起始点，则结束遍历
}
return index;
}
-
分析
1.遍历所有点作为起始点
2.从起始点开始，遍历所有的加油站，判断是否可以开一圈
3.返回index标志位 -
提交结果
135. 分发糖果
老师想给孩子们分发糖果，有 N 个孩子站成了一条直线，老师会根据每个孩子的表现，预先给他们评分。
你需要按照以下要求，帮助老师给这些孩子分发糖果：
- 每个孩子至少分配到 1 个糖果。
- 相邻的孩子中，评分高的孩子必须获得更多的糖果。
那么这样下来，老师至少需要准备多少颗糖果呢？
示例 1:
示例 2:
- 解答
public int candy(int[] ratings) {
int res = 0;
int len = ratings.length;
int[] number = new int[len];//记录每个小孩分到的糖果数量
number[0] = 1;//初始化第一个小孩一个糖果
//从前向后遍历
for (int i = 1; i < len; i++) {
//若后一个小孩比前一个小孩分数高，则糖果要比前面一个小孩多一个
if (ratings[i] > ratings[i - 1])number[i] = number[i - 1] + 1;
//否则发给他一个糖果
else number[i] = 1;
}
//从后向前遍历，更新孩子手中应得的糖果
for (int i = len - 2; i >= 0; i--) {
//若前面的小孩比后面的分数高，并且当前手上的糖果数量小于后面那个小孩的糖果数量+1时，则更新该小孩的糖果数量为后面的小孩的糖果数量+1。
if (ratings[i] > ratings[i + 1] && number[i] < number[i+1] +1)
number[i] = number[i+1] +1;
}
//将每个小孩分到的糖果叠加起来
for (int i = 0; i < number.length; i++) {
res += number[i];
}
return res;
}
-
分析
1.第一遍遍历，根据升序的原则，糖果数量以此递增。否则发一颗糖
2.第二遍遍历是考虑从后面往前的情况。更新孩子手中应得的糖果。
例1:孩子的分数为1，3，5，6，4，2
第一遍遍历，分到的糖果为1，2，3，4，1，1
第二遍遍历，分到的糖果为1，2，3，4，2，1
例2:孩子的分数为1，6，10，8，5，4，3，2
第一遍遍历，分到的糖果为1，2，3，1，1，1，1，1
第二遍遍历，分到的糖果为1，2，6，5，4，3，2，1重点关注例1中的得分为6的孩子和例2中的得分为10的孩子，就能知道为什么第二次遍历的时候要判断（number[i] < number[i+1] +1）是否满足
-
提交结果
136. 只出现一次的数字
给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。
说明：
你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗？
示例 1:
示例 2:
- 解答
public int singleNumber(int[] nums) {
int res = 0;
for (int i:nums) {
res ^= i;
}
return res;
}
-
分析
1.异或。相同为0，不同为1
2.所以出现相同的数字两次异或抵消，只留下了出现一次的数字 -
提交结果
137. 只出现一次的数字 II
给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现了三次。找出那个只出现了一次的元素。
说明：
你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗？
示例 1:
示例 2:
- 解答
public int singleNumber(int[] nums) {
int seenOnce = 0, seenTwice = 0;
for (int num : nums) {
seenOnce = ~seenTwice & (seenOnce ^ num);
seenTwice = ~seenOnce & (seenTwice ^ num);
}
return seenOnce;
}
-
分析
1.官方提供的题解，使用两个位掩码，区分出现一次和出现三次的数字。
2.可以发现seen_once保留了出现一次的数字，出现3次的清零了。
由此可以想到每个元素出现k次，仅出现一次数字的解法。
设置k-1个位掩码。例如k等于4的时候，设置3个位
public int singleNumber(int[] nums) {
int seenOnce = 0, seenTwice = 0, seenThird = 0;
for (int num : nums) {
seenOnce = ~seenTwice & ~seenThird & (seenOnce ^ num);//若seenTwice,seenThird,seenForth不改变，改变seenOnce
seenTwice = ~seenOnce & ~seenThird & (seenTwice ^ num);//若seenOnce,seenThird,seenForth不改变，改变seenTwice
seenThird = ~seenOnce & ~seenTwice & (seenThird ^ num);
}
return seenOnce;
}
- 提交结果
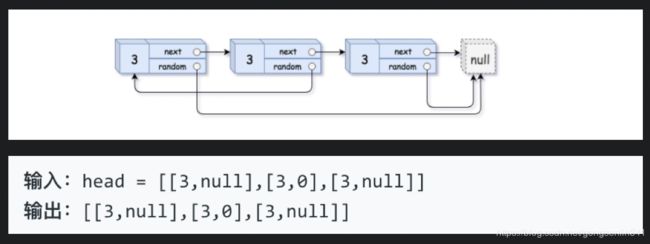
138. 复制带随机指针的链表
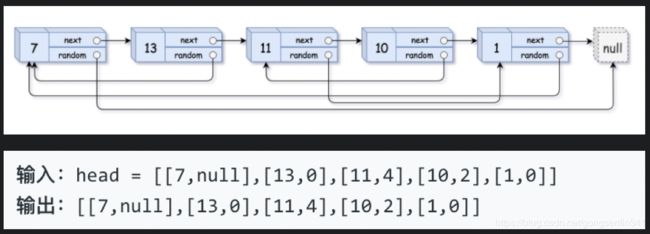
给定一个链表，每个节点包含一个额外增加的随机指针，该指针可以指向链表中的任何节点或空节点。
要求返回这个链表的 深拷贝。
我们用一个由 n 个节点组成的链表来表示输入/输出中的链表。每个节点用一个 [val, random_index] 表示：
- val：一个表示 Node.val 的整数。
- random_index：随机指针指向的节点索引（范围从 0 到 n-1）；如果不指向任何节点，则为 null 。
示例 1：
示例 2：
示例 3：
- 解答
HashMap<Node, Node> map = new HashMap<>();//用于保存结点与拷贝结点的映射关系
public Node copyRandomList(Node head) {
if (head == null) return null;//递归出口
Node newNode = new Node(head.val);//拷贝head结点
map.put(head, newNode);//保留其映射关系
if (!map.containsKey(head.random))//若他随机指向的结点还没有拷贝
newNode.random = copyRandomList(head.random);//则递归拷贝它随机指向的结点
else newNode.random = map.get(head.random);//否则从map中拿到随机指向结点的拷贝对象
if (!map.containsKey(head.next))//若head指向的下一个结点没有拷贝
newNode.next = copyRandomList(head.next);//则递归拷贝它指向的下一个结点
else newNode.next = map.get(head.next);//否则从map中拿到下一个结点的拷贝对象。
return newNode;//返回拷贝对象
}
-
分析
1.利用hashMap来保存已经建立的映射关系，即存储已经拷贝的对象
2.分别判断随机指向的结点和后继结点是否拷贝，若没有拷贝，则递归拷贝它。否则直接从mao中获取已经拷贝的对象。 -
提交结果
139. 单词拆分
给定一个非空字符串 s 和一个包含非空单词列表的字典 wordDict，判定 s 是否可以被空格拆分为一个或多个在字典中出现的单词。
说明：
- 拆分时可以重复使用字典中的单词。
- 你可以假设字典中没有重复的单词。
示例 1：
示例 2：
示例 3：
- 解答
public static boolean wordBreak(String s, List<String> wordDict) {
int maxLen = Integer.MIN_VALUE;//字典中最长的字符串长度
int minLen = Integer.MAX_VALUE;//字段中最短的字符串长度
for (String s1 : wordDict) {
if (s1.length() < minLen)
minLen = s1.length();
if (s1.length() > maxLen)
maxLen = s1.length();
}
boolean[] dp = new boolean[s.length() + 1];//记录第i个字符前的字符串是否可以根据字典划分
dp[0] = true;
for (int i = minLen; i <= s.length(); i++) {//不需要从0开始，比minLen还短的字符串明显不符合字典里的字符串要求。
for (int j = i - maxLen; j < i; j++) {//j也不需要从0开始，判断i-maxLen开始即可，因为是要判断j到i的字符串是否在字典中
if (i - j < minLen) break;
if (j >= 0 && dp[j] && wordDict.contains(s.substring(j, i))) {//若j之前的字符串可以分割为符合字典要求的字符串，并且j到i的字符串在字典中。那么i之前的字符串可以分割为符合字典要求的字符串，设为true
dp[i] = true;
break;
}
}
}
return dp[s.length()];
}
-
分析
1.使用动态规划来实现，dp[i]记录字符串i之前字符串是否可以被分割为符合字典要求的字符串。
2.修改循环判断的起始位置可以大幅度缩短时间。主要是提前求出字典中最短和最长的字符串长度。外层for循环的起始位置是最短字符串长度满足的位置。之前的不用考虑。内层for循环，根据已有的dp[j]求出dp[i]是否满足。则就是考虑j到i的字符串是否在字典中。所以j的起始点，是i - maxLen即可。之前的不用考虑，超出了最大长度。 -
提交结果
140. 单词拆分 II
给定一个非空字符串 s 和一个包含非空单词列表的字典 wordDict，在字符串中增加空格来构建一个句子，使得句子中所有的单词都在词典中。返回所有这些可能的句子。
说明：
- 分隔时可以重复使用字典中的单词。
- 你可以假设字典中没有重复的单词。
示例 1：
示例 2：
示例 3：
- 解答
public static List<String> wordBreak(String s, List<String> wordDict) {
Map<String, List<String>> map = new HashMap<>();
Set<String> dict = new HashSet<>();
for(String str : wordDict) {//换hashset存储，查找效率快
dict.add(str);
}
return helper(s, map, dict);
}
//得到字符串s，分割满足字典中字符串的所有组合
public static List<String> helper(String s, Map<String, List<String>> map, Set<String> dict) {
if(map.containsKey(s)) {//若map中已经有字符串s的分割组合结果 直接返回
return map.get(s);
}
List<String> cur = new ArrayList<>();//创建新的集合链表
if(dict.contains(s)) {//若s包含在字典中，则加入到链表中
cur.add(s);
}
for(int i = 0; i < s.length(); i++) {//遍历字符串s，寻找分割组合
String subRight = s.substring(i);
if(!dict.contains(subRight)) {//从后面找到字典中存在的字符串作为字符串组合的右端部分。
continue;
}
//左端部分递归调用helper寻找组合
List<String> subLeft = helper(s.substring(0, i), map, dict);
//将左端的各种组合和右端部分结合，得到字符串s的分割组合
List<String> tmpp = append(subLeft, subRight);
for(String tt : tmpp) {//添加到集合链表中
cur.add(tt);
}
}
map.put(s, cur);//找到了s的所有的分割组合添加到map中，作为记忆点
return map.get(s);//返回字符串s的分割组合
}
//左端组合结合上右端部分字符串。
public static List<String> append(List<String> tmp, String str) {
List<String> build = new ArrayList<>();
for(String ss : tmp) {
StringBuilder sb = new StringBuilder();
sb.append(ss).append(" ").append(str);
build.add(sb.toString());
}
return build;
}
-
分析
1.遍历字符串s。获得字符串s中所有子串的组合情况。
2.超出字典中字符串最长的长度时候，必定是需要分割的。
通过已经获得的字符串组合，在已有组合的基础上，添加字符串。
例如字典{“a”,“aa”,“aaa”},字符串s=“aaaaaaaa”
遍历字符串s空字符对应的组合情况为空。map中记录<"","">
“a"字符串，遍历它寻找符合字典的子串，因为a满足字典要求，其前面的字符串为”",对应的组合在已有的map的基础上添加字符串"a"，map中添加记录<“a”,“a”>
“aa"字符串，遍历子串发现"aa"符合字典要求，它之前的字符串为”"，获得对应的组合为""，所以在此基础上加上"aa"，map中添加记录<“aa”,“aa”>
继续遍历，发现"a"也符合字典要求，它之前的字符串为"a",获得对应已有的组合为"a"，所在再次基础上加上"a",map中添加记录<“aa”,“a a”>
因为出现了相同的key，所以value可以用集合存起来。
即map中关于"aa"的记录改为<“aa”,"‘aa’,‘a a’">“aaa"字符串，遍历子串，发现"aaa"符合字典要求，它之前的字符串为”"，获得其对应的组合为""，所以在此基础上加上"aaa"，map中添加记录<“aaa”,“aaa”>
继续遍历子串，发现"aa"符合字典要求，它之前的字符串为"a"，获得其对应的组合为"a"，所以在此基础上加上"aa",map中记录为<“aaa”,"‘aaa’,‘a aa’">
继续遍历子串，发现"a"符合字典要求，它之前的字符串为"aa"，获得对应的组合为"‘aa’,‘a a’"，在此基础上加上"a",map中记录为<“aaa”,"‘aaa’,‘a aa’,‘aa a’,‘a a a’">"aaaa"字符串字符串同理，从后面遍历其子串，获得符合字典要求的字符串，在该子串前的字符串的组合情况肯定是之前就找到的。则在这个组合的基础上添加上该字符串。遍历获得所有符合字典要求的字符串，并添加组合后。即可得到"aaaa"字符串的分割组合。
这样一直做到最后就可以获得字符串s的所有分割组合。
-
提交结果
