LeetCode刷题笔记（Java）---第161-180题

162. 寻找峰值

峰值元素是指其值大于左右相邻值的元素。

给定一个输入数组 nums，其中 nums[i] ≠ nums[i+1]，找到峰值元素并返回其索引。

数组可能包含多个峰值，在这种情况下，返回任何一个峰值所在位置即可。

你可以假设 nums[-1] = nums[n] = -∞。

• 解答

    //二分查找
    public int findPeakElement(int[] nums) {
        int left = 0;
        int right = nums.length - 1;
        while (left < right) {
            int mid = (left + right) / 2;
            if (nums[mid] > nums[mid + 1])
                right = mid;
            else left = mid + 1;
        }
        return left;
    }

• 分析

  1.二分查找满足时间复杂度O(logN)
  2.当中间值大于中间值右边一位的时候。说明峰值一定存在左边。所以将right改为mid。
  反之，峰值一定存在右边，left改为mid+1.

• 提交结果
  

164. 最大间距

给定一个无序的数组，找出数组在排序之后，相邻元素之间最大的差值。

如果数组元素个数小于 2，则返回 0。

• 解答

    // 方法一
    public int maximumGap(int[] nums) {
        if (nums.length < 2) return 0;
        int max = Integer.MIN_VALUE;
        Arrays.sort(nums);
        for (int i = 0; i < nums.length - 1; i++) {
            int len = Math.abs(nums[i]-nums[i+1]);
            max = Math.max(max,len);
        }
        return max;
    }
    
    // 方法二
    public int maximumGap2(int[] nums) {
        int len = nums.length;
        if (len < 2) {
            return 0;
        }
        
        int bucketCount = len + 1;
        List<Integer>[] bucket = new ArrayList[bucketCount];
        int min = Integer.MAX_VALUE;
        int max = 0;
        for (int num: nums) {
            min = Math.min(min, num);
            max = Math.max(max, num);
        }

        if (min == max) {
            return 0;
        }

        // 每个桶的大小
        int interval = (int) Math.ceil((max - min) * 1.0 / bucketCount) + 1;

        // 将数组放到各个桶中
        for (int num: nums) {
            int bucketIndex = (num - min) / interval;
            if (bucket[bucketIndex] == null) {
                bucket[bucketIndex] = new ArrayList<>();
            }
            bucket[bucketIndex].add(num);
        }

        //先求第一个桶的最大值
        int prevBucketMax = 0;
        for (Integer num: bucket[0]) {
            prevBucketMax = Math.max(prevBucketMax, num);
        }
        int anxMax = 0;
        for (int i = 1; i < bucketCount; i++) {
            // 求每个桶的最大最小值
            if (bucket[i] == null || bucket[i].isEmpty()) {
                continue;
            }

            int bucketMin = Integer.MAX_VALUE;
            int bucketMax = 0;
            for (Integer num: bucket[i]) {
                bucketMin = Math.min(bucketMin, num);
                bucketMax = Math.max(bucketMax, num);
            }

            int diff = bucketMin - prevBucketMax;
            anxMax = Math.max(anxMax, diff);
            prevBucketMax = bucketMax;
        }

        return anxMax;
    }

• 分析

  1.方法一先排序后比较两两之间的最大差值
  2.方法二使用桶和鸽笼原理。
  首先计算得到数组中的最大值和最小值。
  然后根据最大值和最小值以及数组的长度 求出需要分配桶的个数和每个桶的大小。
  将数组中的值放入到对应的桶中。

  比较桶与桶之间的距离 即前一个桶的最大值和后一个桶的最小值。得到最大的即可。

• 提交结果
  方法一
  
  方法二
  

165. 比较版本号

比较两个版本号 version1 和 version2。
如果 version1 > version2 返回 1，如果 version1 < version2 返回 -1， 除此之外返回 0。

你可以假设版本字符串非空，并且只包含数字和 . 字符。

. 字符不代表小数点，而是用于分隔数字序列。

例如，2.5 不是“两个半”，也不是“差一半到三”，而是第二版中的第五个小版本。

你可以假设版本号的每一级的默认修订版号为 0。例如，版本号 3.4 的第一级（大版本）和第二级（小版本）修订号分别为 3 和 4。其第三级和第四级修订号均为 0。

• 解答

    //方法一
    public static int compareVersion(String version1, String version2) {
        String[] a1 = version1.split("\\.");
        String[] a2 = version2.split("\\.");
        int len = Math.max(a1.length, a2.length);
        for (int n = 0; n < len; n++) {
            int i = (n < a1.length ? Integer.valueOf(a1[n]) : 0);
            int j = (n < a2.length ? Integer.valueOf(a2[n]) : 0);
            if (i < j) return -1;
            else if (i > j) return 1;
        }
        return 0;
    }
    
    //方法二
    public int compareVersion(String version1, String version2) {
        int i = 0;
        int j = 0;
        while (i < version1.length() || j < version2.length()) {
            int a = 0;
            int b = 0;
            while (i < version1.length() && version1.charAt(i) != '.') {
                a = a * 10 + (version1.charAt(i) - '0');
                i++;
            }
            while (j < version2.length() && version2.charAt(j) != '.') {
                b = b * 10 + (version2.charAt(j) - '0');
                j++;
            }
            i++;
            j++;
            if (a > b) return 1;
            else if (a < b) return -1;
        }
        return 0;
    }

• 分析

  1.方法一使用split根据"."划分字符串，依次比较各部分，长度不足的算0.
  2.方法二仅仅是省去了划分的步骤，利用两个指针来获得版本数字，来比较。

• 提交结果
  方法一
  
  方法二
  

166. 分数到小数

给定两个整数，分别表示分数的分子 numerator 和分母 denominator，以字符串形式返回小数。

如果小数部分为循环小数，则将循环的部分括在括号内。

• 解答

    public String fractionToDecimal(int numerator, int denominator) {
        if (numerator == 0) return "0";//若被除数为0，返回0
        StringBuilder stringBuilder = new StringBuilder();
        if (numerator < 0 ^ denominator < 0)//被除数与除数一个为正数一个为负数则结果为负数，前面填上"-"
            stringBuilder.append("-");
        // 精度换成long
        long number1 = Math.abs(Long.valueOf(numerator));
        long number2 = Math.abs(Long.valueOf(denominator));
        // 等到商
        stringBuilder.append(number1 / number2);
        // 得到余数
        long remain = number1 % number2;
        // 若余数为0说明整除直接返回结果
        if (remain == 0) return stringBuilder.toString();
        // 否则说明有小数，先添加一个小数点
        stringBuilder.append(".");
        // 用来记录余数，以及位置
        Map<Long, Integer> map = new HashMap<>();
        while (remain != 0) {
            // 若当前求得余数之前出现过，则说明循环，添加上"()"结束循环
            if (map.containsKey(remain)) {
                stringBuilder.insert(map.get(remain), "(");
                stringBuilder.append(")");
                break;
            }
            // 记录下余数以及可能插入括号的位置
            map.put(remain, stringBuilder.length());
            // 借位，用来继续算除法
            remain = remain * 10;
            // 得到商
            stringBuilder.append(remain/number2);
            // 得到余数
            remain = remain % number2;
        }
        return stringBuilder.toString();
    }

• 分析

  1.利用除法运算规则，如下图：
  
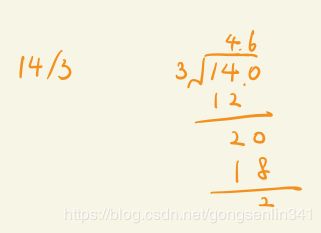
  2.先判断结果是负数还是正数
  3.然后求的商和余数，若余数为0，直接返回商值
  4.若余数不为0，则记录下余数以及可能插入括号的位置。
  借位0，继续算商和余数。
  5.若余数在之前记录过，则说明循环，则在指定位置插入括号。

• 提交结果
  

167. 两数之和 II - 输入有序数组

给定一个已按照升序排列 的有序数组，找到两个数使得它们相加之和等于目标数。

函数应该返回这两个下标值 index1 和 index2，其中 index1 必须小于 index2。

说明:

• 返回的下标值（index1 和 index2）不是从零开始的。
• 你可以假设每个输入只对应唯一的答案，而且你不可以重复使用相同的元素。

• 解答

    public int[] twoSum(int[] numbers, int target) {
        int[] res = new int[2];
        int left = 0;
        int right = numbers.length - 1;
        while (left < right) {
            if (numbers[left] + numbers[right] > target) right--;
            else if (numbers[left] + numbers[right] < target)left++;
            else {
                res[0] = left+1;
                res[1] = right+1;
                break;
            }
        }
        return res;
    }

• 分析

  1.定义两个指针，分别指向数组的开头和末尾
  2.指向循环，当left小于right
  因为数组本身是有序的
  两个指针指向的数字相加，若大于target，则右指针前移。必然会得到比原来小一点的数字，更加的逼近target
  同理 若小于target，则左指针后移。必然会得到比原来的大一点的数字。
  若找到，则直接返回左右指针所指的位置。

• 提交结果
  

168. Excel表列名称

给定一个正整数，返回它在 Excel 表中相对应的列名称。

例如，

• 解答

    public String convertToTitle(int n) {
        String[] letter = new String[]{"", "A", "B", "C", "D", "E", "F", "G", "H", "I", "J", "K", "L", "M", "N", "O", "B", "Q", "R", "S", "T", "U", "V", "W", "X", "Y", "Z"};
        StringBuilder stringBuilder = new StringBuilder();
        while (n > 0) {
            n -= 1;
            stringBuilder.insert(0, letter[1 + n % 26]);
            n /=26;
        }
        return stringBuilder.toString();
    }

• 分析

  1.一开始很自然的考虑就是除以26，余数对应的字母组成列名称。
  例如 1%26 = 1 对应字母A。所以1对应A
  28%26 = 2 对应字母B，28/26 = 1. 1%26 = 1 对应字母A。所以28对应AB。
  2.但当n是26的整数倍的时候会出现问题。
  比如26%26 = 0 26/26 = 1 本该26对应的字母是Z
  但这是如果按照1中的规则 还会判断 1%26 = 1 1/26 = 0. 这里就出现了问题。本该一次判断即可，却进行了两次迭代。
  3.可以考虑n先减一，这样可以避免上述的情况。
  在字母匹配的时候 再把1加回去。
  n -= 1;
  stringBuilder.insert(0, letter[1 + n % 26]);
  n /=26;

  例如26 先减去1 得到25 25%26 = 25 25再加回1 = 26 对应的字母为Z
  25/26 = 0；结束判断。这样只进行了一次判断即可。满足26所对应的字母。

• 提交结果
  

169. 多数元素

给定一个大小为 n 的数组，找到其中的多数元素。多数元素是指在数组中出现次数大于 ⌊ n/2 ⌋ 的元素。

你可以假设数组是非空的，并且给定的数组总是存在多数元素。

• 解答

    public int majorityElement(int[] nums) {
        int num = nums[0];
        int k = 1;
        // 遍历数组
        for (int i = 1; i < nums.length; i++) {
            if(nums[i] == num)k++;
            else if(k==0)num = nums[i];
            else k--;
        }
        return num;
    }

• 分析

  1.简单的逻辑，数字相同k++，数字不同k–。
  k==0时候，num记录新数字。
  最后返回num即可。
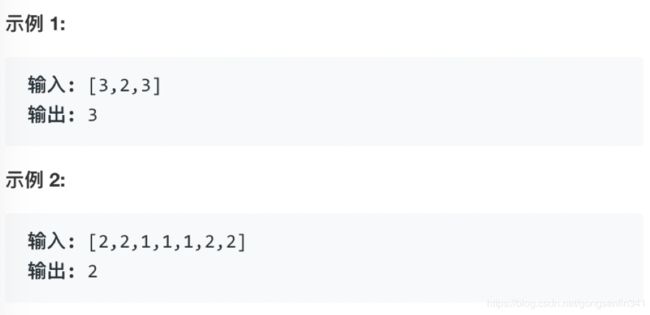
  2.例如：2，2，1，1，1，2，2
  初始化num=2，k=1
  遍历剩余数组 nums[1] == num -> k = 2;
  nums[2] !=num -> k = 1;
  nums[3] !=num -> k = 0;
  因为k=0 -> num = nums[4] = 1;
  因为k=0 -> num = nums[5] = 2;
  num[6] = num -> k = 1;
  最后返回num。

• 提交结果
  

171. Excel表列序号

给定一个Excel表格中的列名称，返回其相应的列序号。

例如，

• 解答

    public static int titleToNumber(String s) {
        int res = 0;
        int index = 0;
        for (int i = s.length() - 1; i >= 0; i--) {
            int num = s.charAt(i) - 64;
            res += num * Math.pow(26, index);
            index++;
        }
        return res;
    }

• 分析

  1.从后面往前遍历字符串，字母对应的数字就是字母对应的ASCII码-64.
  例如 A对应的ASCII码 为65 65-65=1 所以A对应1
  2.这相当于26进制。
  个位即index=0 对应的数字 就是 num * Math.pow(26,0)
  时位即index=0 对应的数字 就是 num * Math.pow(26,1)
  例如"AB"
  B对应的数字是2 ，因为他在个位 所以 2 * Math.pow(26,0) = 2
  A对应的数字是1，因为他在十位 所以 1 * Math.pow(26,1) = 26
  再加起来 得到 28

• 提交结果
  

172. 阶乘后的零

给定一个整数 n，返回 n! 结果尾数中零的数量。

• 解答

    public static int trailingZeroes(int n) {
        int count = 0;
        while(n >= 5) {
            count += n / 5;
            n /= 5;
        }
        return count;
    }

• 分析

  1.两数相乘末尾位0.仅有当各位是2和5的时候，才会得0.
  10！ = （1 * 2 * 3 * （22） * 5 * （23） * 7 * （2 * 2* 2）（33） （25））
  把它拆成这样来看。可以发现2的个数远多于5，所以只要数5的个数就可以知道末尾有多少个0
  2.有几个特殊的情况 例如 25 也可以拆成55 所以25 可以算两个5
  同理 50 可以拆成 25*5 所以也算出现了2个5.
  那么就是计算 乘法因子里有多少个5即可。

• 提交结果
  

173. 二叉搜索树迭代器

实现一个二叉搜索树迭代器。你将使用二叉搜索树的根节点初始化迭代器。

调用 next() 将返回二叉搜索树中的下一个最小的数。

提示：

1 next() 和 hasNext() 操作的时间复杂度是 O(1)，并使用 O(h) 内存，其中 h 是树的高度。
2 你可以假设 next() 调用总是有效的，也就是说，当调用 next() 时，BST 中至少存在一个下一个最小的数。

• 解答

// 方法一
public class BSTIterator {

    private LinkedList<TreeNode> linkedList;

    private int index;

    public BSTIterator(TreeNode root) {
        linkedList = new LinkedList<>();
        index = 0;
        mid(root);
    }

    /**
     * @return the next smallest number
     */
    public int next() {
        int res = linkedList.get(index).val;
        index++;
        return res;
    }

    /**
     * @return whether we have a next smallest number
     */
    public boolean hasNext() {
        return index < linkedList.size();
    }

    public void mid(TreeNode root) {
        if (root == null) return;
        mid(root.left);
        linkedList.add(root);
        mid(root.right);
    }
}
//方法二
class BSTIterator {

    private Stack<TreeNode> stack;


    public BSTIterator(TreeNode root) {
        stack = new Stack<>();
        mid(root);
    }

    /**
     * @return the next smallest number
     */
    public int next() {
        TreeNode node = stack.pop();
        int res = node.val;
        if (node.right != null) {
            mid(node.right);
        }
        return res;
    }

    /**
     * @return whether we have a next smallest number
     */
    public boolean hasNext() {
        return !stack.isEmpty();
    }

    public void mid(TreeNode root) {
        while (root!= null) {
            stack.push(root);
            root = root.left;
        }
    }
}

• 分析

  1.递归实现中序遍历，结果保存在list中，这样next()和hasNext()的时间复杂度可以做到O(1)，但是构建中序遍历序列的时候用到了O(n)的空间复杂度。
  2.考虑使用栈来代替递归，这样可以控制遍历的节奏。先让左孩子，直到左孩子为空。
  这样第一次next()得到的必定是最小的。
  第二次的时候 栈顶出栈。判断是否有右孩子。如果有右孩子的话，那么就右孩子的左孩子入栈，直到叶子结点。返回叶子结点。
  否则直接返回栈顶。
  这样做空间复杂度降低到了O(h) 并且，next()的平均时间复杂度是O(1)

• 提交结果
  //方法一
  
  //方法二
  

174. 地下城游戏

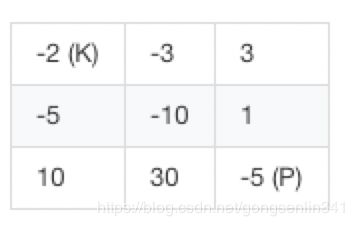
一些恶魔抓住了公主（P）并将她关在了地下城的右下角。地下城是由 M x N 个房间组成的二维网格。我们英勇的骑士（K）最初被安置在左上角的房间里，他必须穿过地下城并通过对抗恶魔来拯救公主。

骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻降至 0 或以下，他会立即死亡。

有些房间由恶魔守卫，因此骑士在进入这些房间时会失去健康点数（若房间里的值为负整数，则表示骑士将损失健康点数）；其他房间要么是空的（房间里的值为 0），要么包含增加骑士健康点数的魔法球（若房间里的值为正整数，则表示骑士将增加健康点数）。

为了尽快到达公主，骑士决定每次只向右或向下移动一步。

编写一个函数来计算确保骑士能够拯救到公主所需的最低初始健康点数。

例如，考虑到如下布局的地下城，如果骑士遵循最佳路径 右 -> 右 -> 下 -> 下，则骑士的初始健康点数至少为 7。

说明:

• 骑士的健康点数没有上限。

• 任何房间都可能对骑士的健康点数造成威胁，也可能增加骑士的健康点数，包括骑士进入的左上角房间以及公主被监禁的右下角房间。

• 解答

    public  int calculateMinimumHP(int[][] dungeon) {
        int height = dungeon.length;
        int width = dungeon[0].length;
        int[][] dp = new int[height][width];
        for (int i = height - 1; i >= 0; i--) {
            for (int j = width - 1; j >= 0; j--) {
                // 终点
                if (i == height - 1 && j == width - 1)
                    dp[i][j] = Math.max(1, -dungeon[i][j] + 1);           
                // 最后一行
                else if (i == height-1)
                    dp[i][j] = Math.max(1,dp[i][j+1] - dungeon[i][j]);
                // 最后一列
                else if (j == width-1)
                    dp[i][j] = Math.max(1,dp[i+1][j] - dungeon[i][j]);
                //其他
                else dp[i][j] = Math.max(1,Math.min(dp[i+1][j],dp[i][j+1]) - dungeon[i][j]);
            }
        }
        return dp[0][0];
    }

• 分析

  1.动态规划
  dp[i][j] 代表从位置i,j出发到达公主位置所需要的初始最少生命值。
  2.从距离公主近的位置开始遍历。
  即从公主位置开始
  dp[height-1][width-1] = Math.max(1,-dungeon[height-1][width-1]+1）
  表示 若公主位置为负数，则返回其相反数+1的值，否则是1.
  例如 -5 则初始生命值需要6

  最后一行的某个位置出发需要的生命值。
  dp[i][j] = Math.max(1,dp[i][j+1] - dungeon[i][j]);

  最后一列的某个位置出发需要的生命值。
  dp[i][j] = Math.max(1,dp[i][j+1] - dungeon[i][j]);

  其余位置，选择右边或下面dp更小的那一个
  dp[i][j] = Math.max(1,Math.min(dp[i+1][j],dp[i][j+1]) - dungeon[i][j]);

• 提交结果
  

175. 组合两个表

编写一个 SQL 查询，满足条件：无论 person 是否有地址信息，都需要基于上述两表提供 person 的以下信息：

FirstName, LastName, City, State

• 解答

select FirstName,LastName,City,State from Person p left join Address a on p.PersonId = a.PersonId;

• 分析

  1.左外连接，显示左表的全部，和右边符合条件的部分

• 提交结果
  

  176. 第二高的薪水

• 解答

//方法一
select distinct Salary as SecondHightestSalary
from Employee
order by Salary desc
limit 1 offset 1
//方法二
select
    (select distinct Salary
     from Employee
     order by Salary desc
     limit 1 offset 1) as SecondHightestSalary
//方法三
select
    ifnull(
        (select distinct Salary
         from Employee
         order by Salary desc
         limit 1 offset 1)
         ,null) as SecondHightestSalary

• 分析

  1.方法一存在的问题，若表中数据仅有一个的时候，则会出现错误。
  2.方法二套了一个子查询，这样判定的时候就不会出错
  3.方法三 ifnull 解决 null 问题

• 提交结果
  方法一出错
  方法二
  
  方法三
  

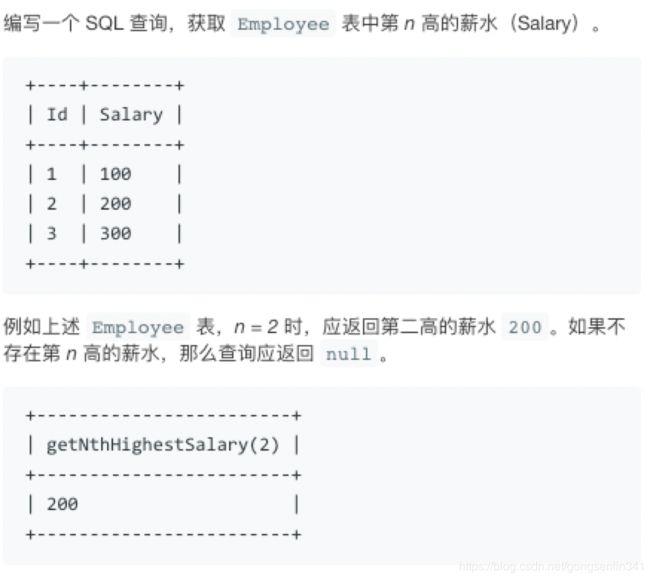
177. 第N高的薪水

• 解答

//方法一
creat function getSecondHighestSalary(N int) return int
begin
    set N = N - 1;
    return (
        select distinct salary
        from Employee
        order by salary desc
        limit N,1
    )
end

//方法二
creat function getSecondHighestSalary(N int) return int
begin
    return(
        select distinct e.salary
        from employ e
        where
            (select count(distinct salary)
             from employee
             where salary > e.salary) = N - 1
    )
end

• 分析

  1.方法一和上一题类似，
  2.方法二 找到N-1个更高的薪水，返回第N高的薪水

• 提交结果
  方法一
  
  方法二
  

178. 分数排名

• 解答

select a.Score as Score,
(select count(distinct b.Score) from Scores b where b.Score >= a.Score) as "Rank"
from Scores a
order by a.Score DESC

• 分析

  1.第一列根据分数降序排列
  2.第二列计算每个分数比自身大的个数，作为排名

• 提交结果
  

179. 最大数

给定一组非负整数，重新排列它们的顺序使之组成一个最大的整数。

• 解答

    public static String largestNumber(int[] nums) {
        if (nums == null || nums.length == 0) {
            return "";
        }
        //转字符串数组
        String[] strArr = new String[nums.length];
        for (int i = 0; i < strArr.length; i++) {
            strArr[i] = String.valueOf(nums[i]);
        }
        //重写排序规则
        Arrays.sort(strArr, new Comparator<String>() {
            @Override
            public int compare(String o1, String o2) {
                return (o2 + o1).compareTo((o1 + o2));
            }
        });
        if(strArr[0]=='0')
            return "0";
        //依次拼接
        StringBuilder sb = new StringBuilder();
        for (String aStrArr : strArr) {
            sb.append(aStrArr);
        }
        String result = sb.toString();
        return result;
    }

• 分析

  1.重写排序规则，当两个数字A，B拼接起来
  若A+B小于B+A，则交换A和B的位置。

• 提交结果
  

180. 连续出现的数字

• 解答

select distinct a.Num as ConsecutiveNums
from Logs as a,Logs as b,Logs as c
where a.Num=b.Num and b.Num=c.Num and a.id=b.id-1 and b.id=c.id-1;

• 分析

  1.查找连续3个id，且值相等的数值

• 提交结果