LeetCode刷题笔记（Java）---第141-160题
文章目录
- 141. 环形链表
- 142. 环形链表 II
- 143. 重排链表
- 144. 二叉树的前序遍历
- 145. 二叉树的后序遍历
- 146. LRU缓存机制
- 147. 对链表进行插入排序
- 148. 排序链表
- 149. 直线上最多的点数
- 150. 逆波兰表达式求值
- 151. 翻转字符串里的单词
- 152. 乘积最大子数组
- 153. 寻找旋转排序数组中的最小值
- 154. 寻找旋转排序数组中的最小值 II
- 155. 最小栈
- 160. 相交链表
141. 环形链表
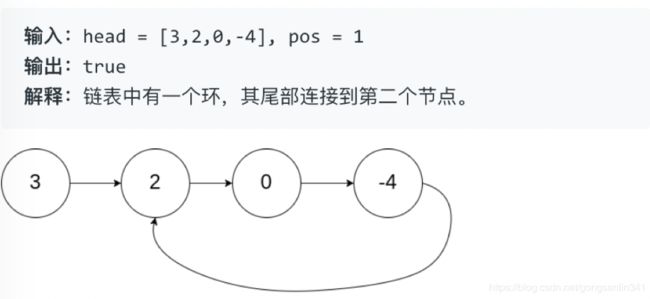
给定一个链表，判断链表中是否有环。
为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。
示例 1：
示例 2：
- 解答
public boolean hasCycle(ListNode head) {
if (head == null) return false;
while (head.next != null){
if(head.val==Integer.MAX_VALUE)//若遍历的当前结点为之前修改过的值，则说明有环
return true;
head.val = Integer.MAX_VALUE;//修改结点的值
head = head.next;
}
return false;
}
public boolean hasCycle(ListNode head) {
if (head == null) return false;
Set<ListNode> set = new HashSet<>()//HashSet来存储已经遍历过的结点;
while (head.next != null) {
if (set.contains(head))
return true;
else set.add(head);
head = head.next;
}
return false;
}
public boolean hasCycle(ListNode head) {
if (head == null) {
return false;
}
ListNode slow = head;
ListNode fast = head.next;
// 快慢指针遍历
while (fast != null && fast.next != null) {
if (slow.equals(fast)) {
return true;
}
slow = slow.next;
fast = fast.next.next;
}
return false;
}
-
分析
1.方法一，修改结点的值，前提是这个值在链表中没有出现，所以这就属于一种投机的做法，遍历结点。若当前结点的值为修改的值则说明有环。
2.方法二，HashSet来存储已经遍历过的结点，若再一次出现已经遍历过的结点则说明有环
3.方法三，设置快慢指针，一个指针移动一个结点，一个指针移动两个结点。若有环，则肯定会出现两个指针指向同一个结点的情况。否则会结束while循环 -
提交结果
方法一
方法二
方法三
142. 环形链表 II
给定一个链表，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。
为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。
说明：不允许修改给定的链表。
示例 1：
- 解答
public ListNode detectCycle(ListNode head) {
if (head == null) return head;
ListNode p = head;
Set<ListNode> set = new HashSet<>();//利用HashSet来存储已经遍历过的结点。
while (p.next != null) {//遍历链表若发出现已经存在集合中的结点则说明是入口结点，返回它
if (set.contains(p))
return p;
else set.add(p);
p = p.next;
}
return null;
}
//利用快慢指针
public ListNode detectCycle2(ListNode head) {
ListNode slow = head;
ListNode fast = head;
ListNode meet = null;
//首先找到相遇的位置，记录下来
while (fast!=null && fast.next!=null){
if(slow == fast) {
meet = fast;
break;
}
fast = fast.next.next;
slow = slow.next;
}
slow = null;
//一个指针从头结点出发，一个指针从相遇结点出发，移动相同的距离后相遇则此时的结点为入口结点。
if(meet!=null){
while (true){
if(meet==slow)
return slow;
slow = slow.next;
meet = meet.next;
}
}
return meet;
}
-
分析
1.方法一和上一题类似
2.方法二看下图：
假设头结点到入口结点的距离为n。慢指针走到入口结点的时候。快指针已经走了2n的距离。距离入口结点的距离上半部分为n。设下半部分为m。
此时慢指针再走m的距离。则快指针走2m的距离，可以发现此时两个指针相遇。即为meet。
由图可知相遇结点距离入口结点的距离也是n。
所以从头结点到入口结点和相遇结点到入口结点的距离是一样的。
此时只需要头结点的位置和相遇结点的位置同时出发，那么他们两个指针相遇的时候，即可得到入口结点。 -
提交结果
方法一：
方法二：
143. 重排链表
给定一个单链表 L：L0→L1→…→Ln-1→Ln ，
将其重新排列后变为： L0→Ln→L1→Ln-1→L2→Ln-2→…
你不能只是单纯的改变节点内部的值，而是需要实际的进行节点交换。
示例 1:
示例 2:
- 解答
//方法一。利用4个指针。分别指向末尾结点。末尾结点的前驱。插入位置的结点。插入位置结点的后继。
public static void reorderList(ListNode head) {
if (head == null || head.next == null || head.next.next == null) return;
ListNode pre = head;
ListNode p = head.next;
ListNode preTail = findTailPre(head);
ListNode tail = preTail.next;
while (p != null && p != tail) {
preTail.next = null;
tail.next = p;
pre.next = tail;
pre = p;
p = pre.next;
preTail = findTailPre(head);
tail = preTail.next;
}
}
//寻找末尾结点的前驱
public static ListNode findTailPre(ListNode head) {
if (head.next == null) return null;
ListNode p = head.next;
ListNode pre = head;
while (p.next != null) {
pre = p;
p = p.next;
}
return pre;
}
//方法二
public static void reorderList(ListNode head) {
if (head == null || head.next == null || head.next.next == null) return;
ListNode pre = head;
ListNode p = head.next;
ListNode mid = findMidNode(head);//计算出中点位置。
//每次从中点位置开始查找尾巴结点和他的后继
ListNode preTail = findTailPre(mid);
ListNode tail = preTail.next;
while (p != null && p != tail) {
preTail.next = null;
tail.next = p;
pre.next = tail;
pre = p;
p = pre.next;
preTail = findTailPre(mid);//每次从中点位置开始查找尾巴结点和他的后继
if (preTail == null || preTail.next == null)
break;
tail = preTail.next;
}
}
public static ListNode findTailPre(ListNode head) {
if (head.next == null) return null;
ListNode p = head.next;
ListNode pre = head;
while (p.next != null) {
pre = p;
p = p.next;
}
return pre;
}
//用快慢指针寻找中心位置。
public static ListNode findMidNode(ListNode head) {
ListNode slow = head;
ListNode fast = head;
while (fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
}
return slow;
}
//方法三
public static void reorderList2(ListNode head) {
if (head == null) {
return;
}
//存到 list 中去
List<ListNode> list = new ArrayList<>();
while (head != null) {
list.add(head);
head = head.next;
}
//头尾指针依次取元素
int i = 0, j = list.size() - 1;
while (i < j) {
list.get(i).next = list.get(j);//头部的元素后继指向尾部元素
i++;//头部指针i指向下一个结点
//偶数个节点的情况，会提前相遇
if (i == j) {
break;
}
//尾部元素的后继指向头部指针结点
list.get(j).next = list.get(i);
j--;//尾巴指针前移。
}
list.get(i).next = null;
}
//方法四
public void reorderList(ListNode head) {
if (head == null || head.next == null || head.next.next == null) {
return;
}
//找中点
ListNode mid = findMidNode(head);
ListNode newHead = mid.next;//后一部分成为新链表
mid.next = null;
newHead = reverseList(newHead);//第二个链表倒置
//链表节点依次连接
while (newHead != null) {
ListNode temp = newHead.next;
newHead.next = head.next;
head.next = newHead;
head = newHead.next;
newHead = temp;
}
}
private ListNode reverseList(ListNode head) {
if (head == null) {
return null;
}
ListNode tail = head;
head = head.next;
tail.next = null;
while (head != null) {
ListNode temp = head.next;
head.next = tail;
tail = head;
head = temp;
}
return tail;
}
public ListNode findMidNode(ListNode head) {
ListNode slow = head;
ListNode fast = head;
while (fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
}
return slow;
}
-
分析
1.方法一在每一次的修改末尾结点的连接关系后。又要重新的寻找末尾结点和它的前驱。这里会浪费很多时间。于是在这里进行改进。搜索的起始位置改为原来链表的中点。因为只有原来链表的后一半需要前移到相应的位置。于是有了方法二
2.方法二在方法一的指向时间上缩短了.但效率还是很低。那么如何可以不用去寻找末尾结点和它的后继呢。那就是事先把他们存储起来。
3.方法三省去了查找尾巴结点需要的时间，但在存储一开始的链表的时候也需要开销。
4.方法四是本题最灵活的思考方式。先分成两个链表。第二个链表倒转，再将两个链表依次连接。例如原来链表顺序为1，2，3，4，5
那么分成两个 分别为1，2，3；4，5
第二个链表倒转为5，4
然后依次连接得到1，5，2，4，3 -
提交结果
方法一
方法二
方法三
方法四
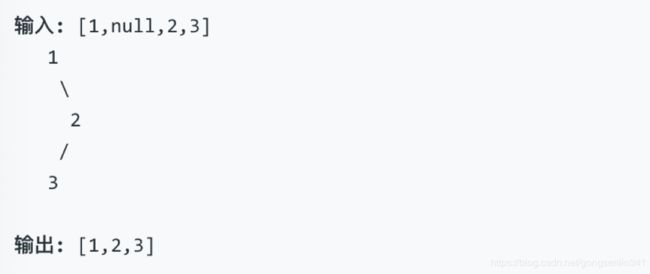
144. 二叉树的前序遍历
给定一个二叉树，返回它的 前序 遍历。
示例:
进阶: 递归算法很简单，你可以通过迭代算法完成吗？
- 解答
//利用栈来实现
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
if (root == null) return res;
Stack<TreeNode> stack = new Stack<>();
stack.add(root);
while (!stack.isEmpty()) {
TreeNode top = stack.pop();
if (top != null) {
res.add(top.val);
stack.add(top.right);
stack.add(top.left);
}
}
return res;
}
-
分析
1.注意栈是先进后出，所以某个结点的孩子入栈顺序应该是右孩子先入栈再左孩子入栈。这样出栈的时候左孩子会比右孩子先出栈。才能做到先序遍历。
-
提交结果
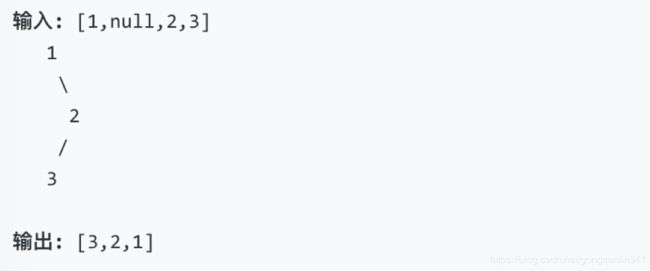
145. 二叉树的后序遍历
给定一个二叉树，返回它的 后序 遍历。
示例:
进阶: 递归算法很简单，你可以通过迭代算法完成吗？
- 解答
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
if (root == null) return res;
Stack<TreeNode> stack1 = new Stack<>();
Stack<TreeNode> stack2 = new Stack<>();
stack1.add(root);
while (!stack1.isEmpty()) {
TreeNode top = stack1.pop();
stack2.add(top);
if (top.left != null)
stack1.add(top.left);
if (top.right != null)
stack1.add(top.right);
}
while (!stack2.isEmpty()) {
res.add(stack2.pop().val);
}
return res;
}
-
分析
1.利用两个栈来实现
根结点入栈。出栈后左右孩子入第一个栈。根结点进第二个栈。
右孩子出栈，右孩子的左右孩子入栈，右孩子进第二个栈。
第一个栈顶出，栈顶孩子结点按照左右的顺序依次入第一个栈。出栈的结点进入第二个栈。
以此类推。第二个栈中就记录了后序遍历的结点顺序。 -
提交结果
146. LRU缓存机制
运用你所掌握的数据结构，设计和实现一个 LRU (最近最少使用) 缓存机制。它应该支持以下操作： 获取数据 get 和 写入数据 put 。
获取数据 get(key) - 如果密钥 (key) 存在于缓存中，则获取密钥的值（总是正数），否则返回 -1。
写入数据 put(key, value) - 如果密钥已经存在，则变更其数据值；如果密钥不存在，则插入该组「密钥/数据值」。当缓存容量达到上限时，它应该在写入新数据之前删除最久未使用的数据值，从而为新的数据值留出空间。
进阶:
你是否可以在 O(1) 时间复杂度内完成这两种操作？
示例:
- 解答
//方法一
public class LRUCache {
private int capacity;
private LinkedList<Integer> linkedList = new LinkedList<>();
private HashMap<Integer, Integer> map = new HashMap<>();
public LRUCache(int capacity) {
this.capacity = capacity;
}
public int get(int key) {
int number = -1;
if (map.containsKey(key)) {
number = map.get(key);
if (linkedList.contains(key))
linkedList.remove(Integer.valueOf(key));
linkedList.add(key);
}
return number;
}
public void put(int key, int value) {
if (map.containsKey(key)) {
map.put(key, value);
linkedList.remove(Integer.valueOf(key));
linkedList.add(key);
} else
{
if (linkedList.size() >= capacity) {
int first = linkedList.getFirst();
map.remove(first);
linkedList.remove(0);
}
linkedList.add(key);
map.put(key, value);
}
}
}
//方法二
public class LRUCache {
class DLinkedNode {
int key;
int value;
DLinkedNode prev;
DLinkedNode next;
}
private void addNode(DLinkedNode node) {
node.prev = head;
node.next = head.next;
head.next.prev = node;
head.next = node;
}
private void removeNode(DLinkedNode node) {
DLinkedNode prev = node.prev;
DLinkedNode next = node.next;
prev.next = next;
next.prev = prev;
}
private void moveToHead(DLinkedNode node) {
removeNode(node);
addNode(node);
}
private DLinkedNode popTail() {
DLinkedNode res = tail.prev;
removeNode(res);
return res;
}
private HashMap<Integer, DLinkedNode> cache = new HashMap<>();
private int size;
private int capacity;
private DLinkedNode head, tail;
public LRUCache(int capacity) {
this.size = 0;
this.capacity = capacity;
head = new DLinkedNode();
tail = new DLinkedNode();
head.next = tail;
tail.prev = head;
}
public int get(int key) {
DLinkedNode node = cache.get(key);
if (node == null) return -1;
moveToHead(node);
return node.value;
}
public void put(int key, int value) {
DLinkedNode node = cache.get(key);
if (node == null) {
DLinkedNode newNode = new DLinkedNode();
newNode.key = key;
newNode.value = value;
cache.put(key, newNode);
addNode(newNode);
++size;
if (size > capacity) {
DLinkedNode tail = popTail();
cache.remove(tail.key);
--size;
}
} else {
node.value = value;
moveToHead(node);
}
}
}
- 分析
方法一
1.链表用于记录访问的顺序。
2.map用来存放key和对应的value。
但这每次更新访问顺序的时候需要耗费时间。做不到O(1)的事件复杂度。所以可以在构造一个对象双向链表。该对象记录着前驱和后继，这样链表中删除的时候，就不需要遍历链表。直接修改对象的指针即可，见方法二。
方法二
构造一个双端队列+HashMap来记录访问顺序以及数据。
get方法从map中寻找key对应的value。若有则返回没有则返回-1.
之后在将该结点移动到队头，表示最近访问。
put方法，若map中已有key则更新value，然后将结点移动到队头。
没有则在队头插入。若队列中的结点数量大于初始容量，则将队尾的结点删除，队尾表示最久没被使用过。同时删除map中对应的键值对。 - 提交结果
方法一
方法二
147. 对链表进行插入排序
对链表进行插入排序。
插入排序的动画演示如上。从第一个元素开始，该链表可以被认为已经部分排序（用黑色表示）。
每次迭代时，从输入数据中移除一个元素（用红色表示），并原地将其插入到已排好序的链表中。
插入排序算法：
插入排序是迭代的，每次只移动一个元素，直到所有元素可以形成一个有序的输出列表。
每次迭代中，插入排序只从输入数据中移除一个待排序的元素，找到它在序列中适当的位置，并将其插入。
重复直到所有输入数据插入完为止。
- 解答
public ListNode insertionSortList(ListNode head) {
ListNode dummy = new ListNode(Integer.MIN_VALUE), pre;
dummy.next = head;
while(head != null && head.next != null) {
if(head.val <= head.next.val) {//跳过有序的部分。
head = head.next;
continue;
}
pre = dummy;
//寻找插入位置。
while (pre.next.val < head.next.val) pre = pre.next;
ListNode curr = head.next;
head.next = curr.next;
curr.next = pre.next;
pre.next = curr;
}
return dummy.next;
}
-
分析
1.用一个辅助头结点来帮助构建新的链表方便会很多
2.原来有序递增的部分不需要重新插入，只需要找到不是递增的结点。然后在从辅助头结点开始遍历，寻找合适的位置插入 -
提交结果
148. 排序链表
在 O(n log n) 时间复杂度和常数级空间复杂度下，对链表进行排序。
示例 1:
示例 2:
- 解答
public ListNode sortList(ListNode head) {
if (head == null || head.next == null) return head;
ListNode slow = head, fast = head.next;
while (fast != null && fast.next != null) {//快慢指针寻找中间结点
slow = slow.next;
fast = fast.next.next;
}
//将链表一分为二
ListNode tmp = slow.next;
slow.next = null;
//递归的寻找最短的链表
ListNode left = sortList(head);
ListNode right = sortList(tmp);
ListNode res = new ListNode(0);
ListNode p = res;
//归并排序
while (left != null && right != null) {
if (left.val < right.val) {
p.next = left;
left = left.next;
} else {
p.next = right;
right = right.next;
}
p = p.next;
}
p.next = left != null ? left : right;
return res.next;
}
-
分析
-
用递归的方式寻找归并排序的最简单的情况。两两合并。
例如8，7，6，5，4，3，2，1。8个结点的链表
拆成两个8，7，6，5；4，3，2，1
再递归拆开8，7；6，5；4，3；2，1
继续递归拆开8；7；6；5；4；3；2；1 -
此时无法再拆 执行下面的while循环。
得到7，8；5，6；3，4；1，2 -
返回上一层递归
执行while循环
得到5，6，7，8；1，2，3，4； -
返回上一层递归
执行while循环
得到1，2，3，4，5，6，7，8
结束
-
-
提交结果
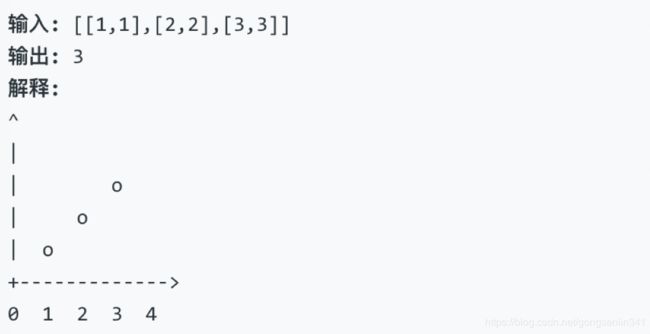
149. 直线上最多的点数
给定一个二维平面，平面上有 n 个点，求最多有多少个点在同一条直线上。
示例 1:
示例 2:
- 解答
public int maxPoints(int[][] points) {
if(points.length <= 2)
return points.length;
int result = 0;
int n = points.length;
Map<String, Integer> map = new HashMap<>();
for(int i = 0; i < n; i++) {
map.clear();
int samePoints = 1;
for(int j = i+1; j < n; j++) {
int dx = points[i][0] - points[j][0];
int dy = points[i][1] - points[j][1];
if( dx == 0 && dy == 0) { // 坐标相同的点
samePoints ++;
continue;
}
// 最大公约数
int gcd = GCD(dx, dy);
String slope = (dx / gcd) + "#" + (dy / gcd);//避免除法精度缺失的问题
if(! map.containsKey(slope))//用map记录这个斜率出现的次数
map.put(slope, 1);
else
map.put(slope, map.get(slope) + 1);
}
if(map.isEmpty()) {
if(samePoints > result)
result = samePoints;
}else {
for(int num : map.values()) {
if(num + samePoints > result)
result = num + samePoints;
}
}
}
return result;
}
private int GCD(int a, int b) {
return ( b == 0) ? a : GCD(b, a % b);
}
-
分析
1.计算斜率。遍历结点，map记录下所有斜率相同出现的次数，表示在同一直线上。
2.String slope = (dx / gcd) + “#” + (dy / gcd)。横纵坐标的差除以最大公约数。避免直接横纵坐标相除，即避免除法精度缺失。 -
提交结果
150. 逆波兰表达式求值
根据逆波兰表示法，求表达式的值。
有效的运算符包括 +, -, *, / 。每个运算对象可以是整数，也可以是另一个逆波兰表达式。
说明：
- 整数除法只保留整数部分。
- 给定逆波兰表达式总是有效的。换句话说，表达式总会得出有效数值且不存在除数为 0 的情况。
示例 1：
示例 2：
- 解答
//方法一
public static int evalRPN(String[] tokens) {
Stack<Integer> res = new Stack<>();
Integer number1, number2;
for (String s : tokens) {
switch (s) {
case "+":
number2 = res.pop();
number1 = res.pop();
res.push(number1 + number2);
break;
case "-":
number2 = res.pop();
number1 = res.pop();
res.push(number1 - number2);
break;
case "*":
number2 = res.pop();
number1 = res.pop();
res.push(number1 * number2);
break;
case "/":
number2 = res.pop();
number1 = res.pop();
res.push(number1 / number2);
break;
default:
res.push(Integer.valueOf(s));
break;
}
}
return res.pop();
}
//方法二 用纯数字来模拟栈，
public static int evalRPN2(String[] tokens) {
int[] stack = new int[tokens.length / 2 + 1];
int index = 0;
for (String s : tokens) {
switch (s){
case "+":
stack[index-2] += stack[--index];
break;
case "-":
stack[index-2] -= stack[--index];
break;
case "*":
stack[index-2] *= stack[--index];
break;
case "/":
stack[index-2] /= stack[--index];
break;
default:
stack[index++] = Integer.valueOf(s);
break;
}
}
return stack[0];
}
-
分析
1.利用栈先进后出，数字先入栈，当遇到运算符的时候。栈顶的两个数字出栈并计算。
2.值得注意的是两个出栈的数字，哪一个是在运算符前哪一个在运算符后面。
3.方法二是看了题解之后学到的。利用纯数组来模拟栈的实现。 -
提交结果
方法一
方法二
151. 翻转字符串里的单词
给定一个字符串，逐个翻转字符串中的每个单词。
说明：
-
无空格字符构成一个单词。
-
输入字符串可以在前面或者后面包含多余的空格，但是反转后的字符不能包括。
-
如果两个单词间有多余的空格，将反转后单词间的空格减少到只含一个。
-
解答
//方法一
public String reverseWords(String s) {
s = s.trim();
String[] strings = s.split("\\s+");
for (int i = 0; i < strings.length / 2; i++) {
String tmp = strings[i];
strings[i] = strings[strings.length-1-i];
strings[strings.length-1-i] = tmp;
}
return String.join(" ",strings);
}
//方法二
public String reverseWords(String s) {
int len = 0;
int i = s.length() - 1;
StringBuilder stringBuilder = new StringBuilder();
while (i >= 0) {
if (s.charAt(i) == ' ') {
if (len == 0)
i--;
else {
stringBuilder.append(s.substring(i + 1, i + 1 + len)).append(" ");
i--;
len = 0;
}
} else {
i--;
len++;
}
}
if (len != 0) stringBuilder.append(s.substring(0, len));
return stringBuilder.toString().trim();
}
-
分析
- 方法一
- 使用trim()去除首尾空格
- split("\s+")，根据一个或多个空格划分字符串
- 首尾交换
- Sting.join 组合字符串。
- 方法二
不使用split，从后面遍历字符串。记录长度已经相应的下标，直到遇到空格，并且记录长度不为空，则说明找到一个字符串。加入到StringBuilder中。
- 方法一
-
提交结果
方法一
方法二
152. 乘积最大子数组
给你一个整数数组 nums ，请你找出数组中乘积最大的连续子数组（该子数组中至少包含一个数字），并返回该子数组所对应的乘积。
- 解答
public int maxProduct(int[] nums) {
if (nums.length == 1) return nums[0];
int[] dpMax = new int[nums.length];//第i个数字结尾的最大乘积
int[] dpMin = new int[nums.length];//第i个数字结尾的最小乘积
dpMax[0] = nums[0];
int max = dpMax[0];
// 遍历nums。更新最大最小乘积数组，以及最大值max
for (int i = 1; i < nums.length; i++) {
dpMax[i] = Math.max(dpMin[i-1]*nums[i],Math.max(dpMax[i-1]*nums[i],nums[i]));
dpMin[i] = Math.min(dpMin[i-1]*nums[i],Math.min(dpMax[i-1]*nums[i],nums[i]));
max = Math.max(max, dpMax[i]);
}
return max;
}
//方法二
public int maxProduct2(int[] nums) {
int res = Integer.MIN_VALUE;
int max = 1;
//正遍历
for (int i = 0; i < nums.length; i++) {
if (nums[i] == 0) {//遇到0，则重置
max = 1;
res = Math.max(0, res);
}
else {//一直累成计算最大值
max = max * nums[i];
res = Math.max(max, res);
}
}
max = 1;
//倒遍历，同理
for (int i = nums.length - 1; i >= 0; i--) {
if (nums[i] == 0)
max = 1;
else {
max = max * nums[i];
res = Math.max(max, res);
}
}
return res;
}
-
分析
- 方法一
1.第i个数字结尾的子数组。
若第i个数字为正数，那么dpMax[i-1]大于0的话。那么dpMax[i]就等于dpMax[i-1] * nums[i];否则就是本身。
2.若第i个数字为负数，此时如果仅有dpMax数组的话，不能得到这一位结尾的子数组的最大乘积。所以需要dpMin数组来记录第i个数字结尾的子数组的最小乘积。负负得正嘛。
所以若dpMin[i-1]小于0的话，那么dpMax[i]就等于
dpMin[i-1]*nums[i]。
综上得
dpMax[i] = Math.max(dpMin[i-1]*nums[i],Math.max(dpMax[i-1]*nums[i],nums[i]));
dpMin[i] = Math.min(dpMin[i-1]*nums[i],Math.min(dpMax[i-1]*nums[i],nums[i]));
最后返回dpMax中的最大值 - 方法二
1.数字的累乘，都是正数的话，是越多越好。出现负数的时候，若负数的个数是偶数，全部相乘最大。若负数的个数是奇数的时候。则去掉首尾其中一个负数累乘的结果最大。所以需要正着遍历一次，倒着遍历一次，计算最大值。
2.当出现0的时候，相当于划分数组。0的前半部分和后半部分，分别计算最大值。即代码中修改max=1.表示重新计算。
- 方法一
-
提交结果
方法一
方法二
153. 寻找旋转排序数组中的最小值
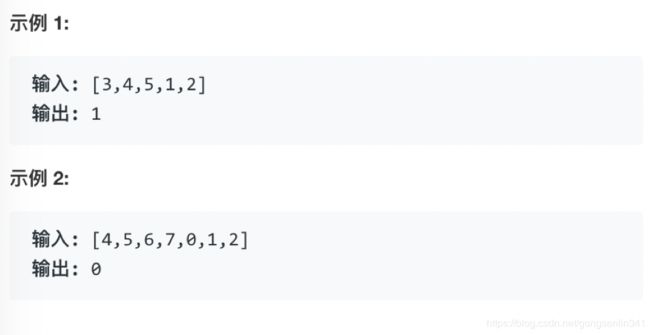
假设按照升序排序的数组在预先未知的某个点上进行了旋转。
( 例如，数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。
请找出其中最小的元素。
你可以假设数组中不存在重复元素。
- 解答
public static int findMin(int[] nums) {
int left = 0;
int right = nums.length - 1;
int min = Integer.MAX_VALUE;
while (left < right) {
int mid = (left + right) / 2;
//中间值不是左右指针指向的值
if (mid != left && mid != right)
//若中间值小于左右指针指向的值。则中间值和min比较记录更小的值。修改right为mid-1.
if (nums[mid] < nums[left] && nums[mid] < nums[right]) {
min = Math.min(min, nums[mid]);
right = mid - 1;
}
// 若中间值大于左右指针的值，那么最小值一定在右边
else if (nums[mid] > nums[left] && nums[mid] > nums[right]) {
left = mid + 1;
}
// 其他 说明左指针的值小于中间值，则直接返回和min最比较后更小的值
else {
return Math.min(min, nums[left]);
}
// 若中间值是左右指针指向的值，则直接比较左右指针指向的值哪个更小，然后返回和min最比较后更小的值
else {
return nums[left] < nums[right] ? Math.min(min, nums[left]) : Math.min(min, nums[right]);
}
}
return Math.min(min, nums[left]);
}
-
分析
1.首先定义左右指针指向首尾
2.得到中间值，若中间值和其中一个指针重复，说明此时待比较的数组仅有2个，那么直接比较这两个谁小即可。
3.因为是升序数组旋转后的数组。所以仅有三种情况。a.中间值比左右指针小，如7,0,1,2,4,5,6。中间值是2，小于左右指针的值。此时比较min和中间值，记录更小的一个。这是为了避免此时中间值就是要找的最小值。 之后的最小值一定在左边，所以修改right为mid-1。 b.中间值比左右指针大，如3，4，5，1，2。中间值是5，大于左右指针的值。此时最小值一定在右边，修改left为mid+1 c.左指针比中间值小，此时说明数组是升序的。返回左指针和min中记录的两者中较小者。 -
提交结果
154. 寻找旋转排序数组中的最小值 II
假设按照升序排序的数组在预先未知的某个点上进行了旋转。
( 例如，数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。
请找出其中最小的元素。
注意数组中可能存在重复的元素。
- 解答
public static int findMin2(int[] nums) {
int left = 0;
int right = nums.length - 1;
int min = Integer.MAX_VALUE;
while (left < right) {
int mid = (left + right) / 2;
if (mid != left && mid != right) {
while (left < mid && right > mid && nums[mid] == nums[left] && nums[mid] == nums[right]) {
left++;
right--;
}
min = Math.min(min, nums[mid]);
if ((nums[mid] < nums[left] && nums[mid] < nums[right]) || (nums[left] > nums[mid] && nums[mid] == nums[right])) {
right = mid - 1;
} else if ((nums[mid] > nums[left] && nums[mid] > nums[right]) || (nums[left] == nums[mid] && nums[mid] > nums[right])) {
left = mid + 1;
} else {
return Math.min(min, nums[left]);
}
} else {
return nums[left] < nums[right] ? Math.min(min, nums[left]) : Math.min(min, nums[right]);
}
}
return Math.min(min, nums[left]);
}
-
分析
相比较于上一题。多了三个地方的判断
第一：当中间值同时和左右两个值相等的时候，则左右指针向中间值靠拢，移动一位。
第二：当中间值和右边相等，且左边的值大于中间值时候，则最小值可能出现在左侧，则修改右指针为mid-1；
例如2，0，1，1，1
第三：当中间值和左边相等，且右边的值小于中间值的时候，则最小值可能出现在右侧，则修改左指针为mid+1. -
提交结果
155. 最小栈
设计一个支持 push ，pop ，top 操作，并能在常数时间内检索到最小元素的栈。
- push(x) —— 将元素 x 推入栈中。
- pop() —— 删除栈顶的元素。
- top() —— 获取栈顶元素。
- getMin() —— 检索栈中的最小元素。
提示：
pop、top 和 getMin 操作总是在 非空栈 上调用。
- 解答
public class MinStack {
private LinkedList<Integer> linkedList;//用于模拟栈
private LinkedList<Integer> minLinkedList;//用于保存最小值。
/**
* initialize your data structure here.
*/
public MinStack() {
minLinkedList = new LinkedList<>();
linkedList = new LinkedList<>();
}
public void push(int x) {
//当最小值栈为空 或者x小于最小值栈的栈顶元素时候入栈，栈顶为更小的值
if (minLinkedList.size()==0 || x <= minLinkedList.get(minLinkedList.size() - 1)) minLinkedList.add(x);
// x入数据栈
linkedList.add(x);
}
public void pop() {
// 若出栈的元素和最小值栈栈顶元素一样，则最小值栈栈顶出栈
if (linkedList.get(linkedList.size() - 1).intValue() == minLinkedList.get(minLinkedList.size() - 1).intValue())
minLinkedList.removeLast();
// 数据栈栈顶出栈
linkedList.removeLast();
}
public int top() {
return linkedList.get(linkedList.size() - 1);
}
public int getMin() {
return minLinkedList.get(minLinkedList.size() - 1);
}
}
-
分析
1.用一个仅保存最小值的栈来记录曾经以及现在的最小值。距离栈顶越近的越小。
2.出栈的时候判断是否是最小值出栈，更小最小值栈。 -
提交结果
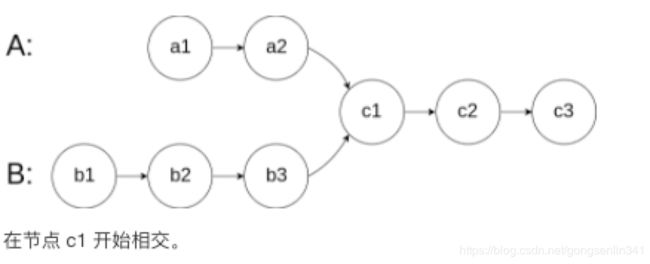
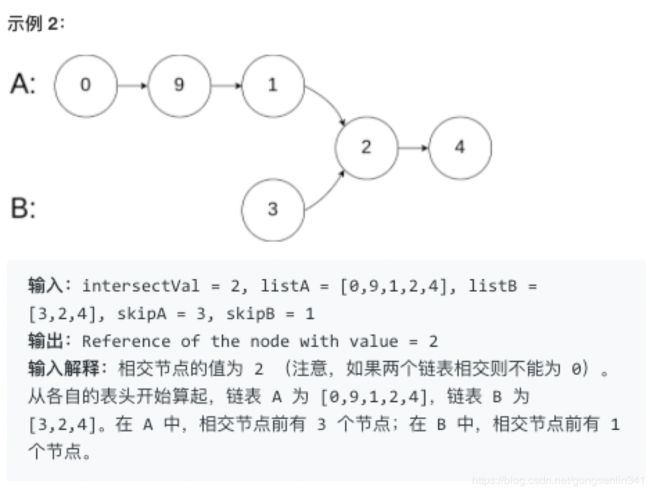
160. 相交链表
编写一个程序，找到两个单链表相交的起始节点。
如下面的两个链表：
- 解答
public static ListNode getIntersectionNode(ListNode headA, ListNode headB) {
if (headA == headB) return headA;
if (headA == null || headB == null) return null;
int lenA = 1;
ListNode p = headA;
// 计算链表a的长度
while (p.next != null) {
p = p.next;
lenA++;
}
p = headB;
int lenB = 1;
// 计算链表b的长度
while (p.next != null) {
p = p.next;
lenB++;
}
p = headA;
ListNode q = null;
// 长的链表先遍历，直到两个链表长度一致
if (lenA >= lenB) {
while (lenA > lenB) {
lenA--;
p = p.next;
}
q = headB;
} else {
p = headB;
while (lenB > lenA) {
lenB--;
p = p.next;
}
q = headA;
}
//同时遍历剩余链表，寻找重复结点
while (p.next != null && q.next != null) {
if (p.val == q.val && p == q) return p;
p = p.next;
q = q.next;
}
return p == q ? p : null;
}
-
分析
1.先计算两个链表的长度
2.比较两个长度，较长的先遍历，直到两个链表相同长度
3.然后同时遍历剩余链表寻找重复结点。
4.最后会遍历到末尾结点，所以比较末尾结点是否重复，重复则返回，否则返回null。 -
提交结果
