群体智能优化算法之布谷鸟搜索(CS)
获取更多资讯,赶快关注上面的公众号吧!
文章目录
- 第六章 布谷鸟搜索[1]
- 6.1 介绍
- 6.2 人工布谷鸟搜索
- 6.2.1 随机变量
- 6.2.2 随机游走
- 6.2.2.1 幂律
- 6.2.3 赫维赛德函数(阶跃函数)
- 6.2.4 Lévy(莱维)分布
- 6.2.4.1 Lévy飞行
- 6.2.5 布谷鸟搜索的优点
- 6.3 布谷鸟搜索的数学证明
- 6.4 布谷鸟搜索的变种
- 6.4.1 离散布谷鸟搜索
- 6.4.2 改进的布谷鸟搜索
- 6.4.3 二进制布谷鸟搜索
- 6.4.4 混沌布谷鸟搜索(Chaotic Cuckoo Search,CCS)
- 6.4.5 并行布谷鸟搜索
- 6.4.6 高斯布谷鸟搜索
- 参考文献
第六章 布谷鸟搜索[1]
6.1 介绍
布谷鸟(杜鹃)是一种非常迷人的鸟类,它们不仅能发出各种声音或叫声,还能以不同的方式繁殖。杜鹃科中的犀鹃(Ani Cuckoo)和圭拉鹃(Guira Cuckoo),将它们的蛋放在其他鸟的巢中,从此杜鹃鸟的蛋完全依赖于寄主鸟的照料,这就是巢寄生。
如果寄主鸟发现蛋不是它们的,要么把蛋扔掉,要么放弃巢穴,然后寄主鸟再建一个新的巢穴。为了防止这种情况的发生,雌性布谷鸟已经进化到可以模拟寄主蛋的颜色和纹理,从而降低被遗弃的可能性。同时蛋也会分布在不同的巢中,以减少蛋丢失的机会。如果布谷鸟的蛋没有被识别出来,它通常会在寄主鸟蛋之前孵化,并把其他的蛋从巢中踢出去,这样就能分得更多的食物,甚至有些布谷鸟雏鸟也能模仿寄主雏鸟的叫声。
巢寄生的一个好处是,父母不需要投资筑巢或喂养幼鸟。他们可以花更多的时间在捕食和繁殖上。随着时间的推移,自然选择使寄主鸟和布谷鸟都进化了,使得每一代中最适合的鸟存活下来。布谷鸟的这种繁殖行为是协同进化的最佳模型之一,也是最近发展的优化技术,即布谷鸟搜索的基础。
6.2 人工布谷鸟搜索
布谷鸟搜索受布谷鸟的巢寄生行为和一些鸟类和果蝇的莱维(Lévy Flight)行为的启发,是由Xin-She Yang和Suash Deb (2009)[2]提出的一种新型的基于群体的优化技术。
布谷鸟算法源于以下三条规则[3]:
- 每只布谷鸟每次产下一枚蛋,并将其放入随机选择的巢中;
- 具有优质蛋的最佳巢会被进入到下一代;
- 可用的寄主巢数量是固定的,且寄主以概率pa∈(0,1)发现布谷鸟放的蛋。在这种情况下,寄主可以消灭该蛋或放弃旧巢另建新巢。
在进一步研究算法之前,先讨论一些数学术语和函数。
6.2.1 随机变量
任何随机现象的输出都是随机变量,并用X表示。如果一个随机变量只取不同的值,比如1,2,那么它就是离散的;如果它可以在一个区间内取任意值,那它就是连续的。这些通常用曲线下的面积或积分表示。随机变量X在一组结果A上的概率,就是A上和曲线下之间的面积,这条曲线下的总面积必须是1,对于集合A中的任何元素都不应该有负值。这样的曲线称为密度曲线。
6.2.2 随机游走
随机游走(记为SN)是一系列随机步的和,每一步都由一个随机变量Xi表达:
N = ∑ i = 1 N X i = X 1 + … … … + X N (1) N = \sum\limits_{{\rm{i}} = 1}^N {{X_{\rm{i}}}} = {X_1} + \ldots \ldots \ldots + {X_N}\tag 1 N=i=1∑NXi=X1+………+XN(1)
随机游走的长度可以是固定的,也可以是可变的(取决于步长)。
6.2.2.1 幂律
当一个量相对变化时会导致两一个量成比例的相对变化时,需要应用幂律(比例律),幂律分布的一般形式是:
Y = k X α (2) Y = k{X^\alpha }\tag 2 Y=kXα(2)
其中X和Y是目标变量,α是律指数,k为常量。
6.2.3 赫维赛德函数(阶跃函数)
通常用H或θ表示,用于表达分段常数函数或广义函数。
作为分段函数时:
H ( x ) = 0 i f x < 0 = 1 2 i f x = 0 = 1 i f x > 0 (3) \begin{array}{l} H(x) = 0\;\;\;{\rm{if }}x < 0\\ \;\;\;\;\;\;\;\; = \frac{1}{2}\;\;\;{\rm{if }}x = 0\\ \;\;\;\;\;\;\;\; = 1\;\;\;\;{\rm{if }}x > 0 \end{array}\tag 3 H(x)=0ifx<0=21ifx=0=1ifx>0(3)
作为广义函数:
∫ θ ( x ) ϕ ′ ( x ) d x = − ϕ ( 0 ) (4) \int \theta (x){\phi ^\prime }(x)dx = - \phi (0)\tag 4 ∫θ(x)ϕ′(x)dx=−ϕ(0)(4)
简化表示为:
H c ( x ) ≡ ( x − c ) (5) {H_c}(x) \equiv (x - c)\tag 5 Hc(x)≡(x−c)(5)
6.2.4 Lévy(莱维)分布
Lévy分布是非负随机变量的稳定连续概率分布,可以用以下简单的方式表达:
L ( s , γ , μ ) = γ 2 Π exp [ − γ 2 ( s − μ ) ] 1 ( s − μ ) 3 / 2 , 0 < μ < s < ∞ = 0 , o t h e r w i s e (6) \begin{array}{l} L(s,\gamma ,\mu ) = \sqrt {\frac{\gamma }{{2\Pi }}} \exp \left[ { - \frac{\gamma }{{2(s - \mu )}}} \right]\frac{1}{{{{(s - \mu )}^{3/2}}}},\quad 0 < \mu < s < \infty \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{ = }}0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{otherwise}} \end{array}\tag 6 L(s,γ,μ)=2Πγexp[−2(s−μ)γ](s−μ)3/21,0<μ<s<∞=0,otherwise(6)
其中µ是最小步长,γ是尺度参数。
6.2.4.1 Lévy飞行
Lévy飞行是步长服从Lévy分布的随机游走,通过下式表达:
L ( s ) ∣ s ∣ − 1 − β 0 < β ≤ 2 (7) L(s)~|s{|^{ - 1 - \beta }}\quad 0 < \beta \le 2\tag 7 L(s) ∣s∣−1−β0<β≤2(7)
其中β是一个索引。
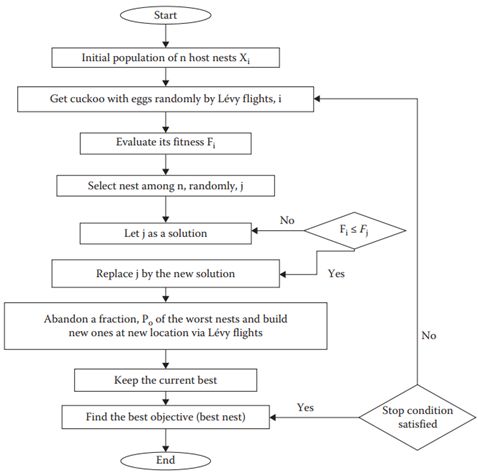
以下为布谷鸟搜索的伪代码和算法流程图。
Begin
目标函数f(I),I=(i1,i2,…,id)T
生成初始种群
for n个寄主巢穴:Ij(j=1,2,…,n)
while(t<MaxGeneration)||(停止准则)
根据Lévy飞行随机选择布谷鸟
计算适应度值Fj
在n中随机选择巢穴(假设为k)
if(Fj>Fk)
使用新解替换k
end
抛弃一小部分(pα)更糟糕的巢穴并建立新巢
保留最优解(或优质解的巢穴)
对解进行排序并考虑最优解
end while
后处理结果和可视化
end
6.2.5 布谷鸟搜索的优点
布谷鸟搜索(CS)有很多优势:
- 布谷鸟搜索在搜索空间探索时,在局部搜索和多样性或随机性之间保持了有效的平衡;
- 布谷鸟只包含两个控制参数:种群大小n和概率pα,使得算法更简单更通用;
- 如果种群大小固定,则仅通过来pα控制精英(将最优解带到下一代以构造新的解)、随机均衡和局部搜索;
- 布谷鸟搜索具有高效的随机化,并有大步长的可能性;
- 收敛率pα与无关,因此对于每一个 新的问题,不需要调整参数;
- 因其通用性可以应用于各种优化问题;
- 在多峰函数上,它的求解优于PSO和GA。
6.3 布谷鸟搜索的数学证明
如前所述,布谷鸟搜索通过Lévy飞行进行全局搜索或探索,飞行中步长可变并且进行突然90°的转弯,偶尔的大步长可以保证搜索不回陷入到局部最优。
该算法执行两种类型的搜索:局部搜索和全局搜索。
局部搜素通过局部随机游走执行:
x i ( t + 1 ) = x i ( t ) + α s ⊗ H ( p a − ε ) ⊗ ( x j ( t ) − x k ( t ) ) (8) x_i^{(t + 1)} = x_i^{(t)} + \alpha s \otimes H\left( {{p_a} - \varepsilon } \right) \otimes \left( {x_j^{(t)} - x_k^{(t)}} \right)\tag 8 xi(t+1)=xi(t)+αs⊗H(pa−ε)⊗(xj(t)−xk(t))(8)
其中xj和xk为随机选择的解,H(µ)为赫维赛德函数,pα是用于平衡局部和全局随机游走的切换参数,s为步长,ε为均匀分布的随机数。
全局搜索通过Lévy飞行执行:
x i ( t + 1 ) = x i ( t ) + α L ( s , λ ) (9) x_i^{(t + 1)} = x_i^{(t)} + \alpha L(s,\lambda )\tag 9 xi(t+1)=xi(t)+αL(s,λ)(9)
其中α>0为步长缩放因子,且
L ( s , λ ) = λ Γ ( λ ) sin ( π λ / 2 ) π 1 s 1 + λ ( s > > s o > 0 ; s o 为 最 小 步 长 ) (10) L(s,\lambda ) = \frac{{\lambda \Gamma (\lambda )\sin (\pi \lambda /2)}}{\pi }\frac{1}{{{s^{1 + \lambda }}}}\quad \left( {s > > {s_o} > 0;{s_{\rm{o}}为最小步长}{\rm{ }}} \right)\tag {10} L(s,λ)=πλΓ(λ)sin(πλ/2)s1+λ1(s>>so>0;so为最小步长)(10)
其中 Γ ( z ) = ∫ 0 ∞ t z − 1 e − t d t \Gamma (z) = \int_0^\infty {{t^{z - 1}}} {e^{ - t}}dt Γ(z)=∫0∞tz−1e−tdt
Lévy飞行是步长服从Lévy分布的随机游走:
L e ′ v y − 1 s λ + 1 0 ≤ λ ≤ 2 (11) {\rm{Le'vy}}-\frac{1}{{{s^{\lambda + 1}}}}\quad 0 \le \lambda \le 2\tag {11} Le′vy−sλ+110≤λ≤2(11)
通过Lévy飞行生成的随机数由通过正太分布创建的随机方向选择组成,步长使用Mantegna算法生成:
s = u ∣ v ∣ 1 / β (12) {\rm{s}} = \frac{u}{{|v{|^{1/\beta }}}}\tag {12} s=∣v∣1/βu(12)
其中µ和ν服从正太分布:
μ ∼ N ( 0 , σ μ 2 ) 和 ν ∼ N ( 0 , σ ν 2 ) (13) \mu \sim N\left( {0,\sigma _\mu ^2} \right)和\nu \sim N\left( {0,\sigma _\nu ^2} \right)\tag {13} μ∼N(0,σμ2)和ν∼N(0,σν2)(13)
σ u = { Γ ( 1 + β ) sin ( β 2 ) Γ [ 1 + β 2 ] β 2 ( β + 1 ) / 2 } 1 / β a n d σ v = 1 (14) {\sigma _{\rm{u}}} = {\left\{ {\frac{{\Gamma (1 + \beta )\sin \left( {\frac{\beta }{2}} \right)}}{{\Gamma \left[ {\frac{{1 + \beta }}{2}} \right]\beta {2^{(\beta + 1)/2}}}}} \right\}^{1/\beta }}{\rm{ and }}{\sigma _v} = 1\tag {14} σu=⎩⎨⎧Γ[21+β]β2(β+1)/2Γ(1+β)sin(2β)⎭⎬⎫1/βandσv=1(14)
设r∈[0,1],与发现/切换概率pα相比得到全局分支:
x i ( t + 1 ) ← x i ( t ) i f r < p α x i ( t + 1 ) ← x i ( t ) + α ⊗ L ( s , λ ) i f r > p α (15) \begin{array}{l} x_i^{(t + 1)} \leftarrow x_i^{(t)}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{if }}r < {p_\alpha }\\ x_i^{(t + 1)} \leftarrow x_i^{(t)} + \alpha \otimes L(s,\lambda )\;\;\;\;{\rm{if }}r > {p_\alpha } \end{array}\tag {15} xi(t+1)←xi(t)ifr<pαxi(t+1)←xi(t)+α⊗L(s,λ)ifr>pα(15)
因为CS算法是一个随机搜索算法,我们可以总结为以下主要步骤:
-
初始种群由n个随机位置的巢构成,X={x10,x20,…,xn0},然后评估它们的目标函数值,以找到当前的全局最佳gt0;
-
由下式更新解:
x i ( t + 1 ) = x i ( t ) + α ⊗ L ( λ ) (16) x_i^{(t + 1)} = x_i^{(t)} + \alpha \otimes L(\lambda )\tag {16} xi(t+1)=xi(t)+α⊗L(λ)(16) -
从均匀分布[0,1]中取随机数r。如果r>pα,则更新xi(t+1)。然后评估新解,找到新的全局最佳gt∗;
-
如果满足停止要求,则gt∗是目前为止发现的最好的全局解。否则,返回步骤2。
6.4 布谷鸟搜索的变种
6.4.1 离散布谷鸟搜索
离散布谷鸟旨在解决像旅行商(TSP)、调度这样的组合问题。组合问题中组合的数量随着问题的规模呈指数增长,解决这样的问题需要大量的计算。
Ouaarab,Ahiod和Yang(2014)[4]针对TSP提出了布谷鸟搜索的离散版本,Ouyang等(2013)[5]提出了求解环形TSP的离散布谷鸟搜索。
6.4.2 改进的布谷鸟搜索
提出的改进将布谷鸟作为控制集中和分散的第一层,种群是第二个控制层。增加了一种新型的更聪明的布谷鸟用于种群重组,这些新的布谷鸟能够改变它们的寄主巢穴以降低被遗弃的机会,这样就有了新的一小部分布谷鸟pc,其首先通过Levy飞行搜索寄主巢穴(新解),然后从当前解寻找更优的解。
以下为改进布谷鸟搜索的伪代码:
Begin
目标函数f(I),I=(i1,i2,…,id)T
生成初始种群
for (n)个巢穴:Ij(j=1,2,…,n)
while(t<MaxGeneration) || (停止准则)
使用一小部分智能布谷鸟(pc)进行搜索
使用Levy飞行随机选择一只布谷鸟
计算其适应度Fj
从hn中随机选择一个巢穴,例如k
if(Fj>Fk)
使用新解替换k
end if
遗弃一小部分(Pa)糟糕的解,构建新的解
记录最优解
end while
结果后处理及可视化
作者在算法中使用了扰动,使用局部扰动使得算法足够灵活,可以适应其他优化问题。
6.4.3 二进制布谷鸟搜索
优化问题可以是连续的,其中解可以用一组实数表示,也可以是离散的,可以用一组整数表示。然而,在二进制优化中,解是由一组位表示的。二进制版本的布谷鸟搜索(BCS)可应用于路由、调度、特征选择等问题。
在使用Levy飞行的原始CS算法中,解表示为连续搜索空间中的实数集合,这些都需要转换成二进制值,以适应离散二进制版本的布谷鸟搜索。BCS有两个主要方面(Pereira等,2014)[6]:
- 二进制布谷鸟动态,包括
-
使用Levy飞行获得新解;
-
二进制解的表达(BSR)以寻找每只布谷鸟移动的可能性。
- 目标函数和选择算子—其原理与遗传算法相同
设xi为[0,1]上具有连续值的解,xi’为二进制表达的解,使用sigmoid函数对值进行转换:
S ( x i ) = 1 1 + e − x i (17) {\rm{S}}\left( {{x_i}} \right) = \frac{1}{{1 + {e^{ - {x_i}}}}}\tag {17} S(xi)=1+e−xi1(17)
其中S(xi)代表xi’的变动机会。
为了确定二进制解xi’,S(xi)在解x的每一维i上与生成的随机数γ比较,如果变动机会大于γ,二进制值为1,否则为0:
f ( n ) = ← { 1 , if γ < S(xi) 0 , otherwise (18) f(n)= \leftarrow \begin{cases} 1, & \text {if $\gamma$ < S({xi})} \\ 0, & \text{otherwise} \end{cases} \tag {18} f(n)=←{1,0,if γ < S(xi)otherwise(18)
6.4.4 混沌布谷鸟搜索(Chaotic Cuckoo Search,CCS)
在CCS中将混沌理论融入到了布谷鸟搜索技术中,混沌理论研究高度敏感系统的行为,其中初始位置的微小变化会对系统的行为产生很大的影响,混沌具有非重复和遍历性的特点,便于快速搜索。同时也引入了遗传算法中的精英概念,将最优布谷鸟代入下一代,以构建新的更优解。Wang等(2016)[7]提出的CCS使用一个混沌可变步长α,可通过归一化的混沌地图(展示混沌行为)进行调整,归一化混沌地图后,其总是在[0,2]内变化。精英可以防止最优布谷鸟随着解的更新变差。
以下是混沌布谷鸟搜索的伪代码:
Begin:
Step 1:初始化。设置代计数器i=1,随机初始化种群P,随机设置pa和混沌地图的初始值c0,以及精英参数KEEP。
Step 2:While t<MaxGeneration
根据适应度值对种群进行排序
KEEP←最优布谷鸟
使用混沌地图更新步长(α=ci+1)
随机选择一个布谷鸟(假如i),通过执行Levy飞行替换该解
计算其适应度值Fi
在n中随机选择一个巢穴(假如k)
if(Fi<Fk)
使用新解替换k
end if
使用新解替换一小部分(pa)糟糕解
使用KEEP个最优布谷鸟替换KEEP个最劣布谷鸟
对种群进行排序以确定当前最优
t=t+1
end while
end
6.4.5 并行布谷鸟搜索
并行化是受自然界启发基于种群算法的自然拓展,Tzy-Luen等(2016)[8]提出了并行布谷鸟搜索。该算法将主种群分解成子种群,从而在搜索解空间时增加了多样性。
并行布谷鸟搜索的伪代码:
Begin
目标函数f(n),n=(n1,…,nd)T
生成n个巢穴的初始主种群np
将种群分解成子种群,每个子种群1…p在相同的搜索空间中并行执行布谷鸟搜索
while(i<停止准则)
子种群1…p并行地
通过Levy飞行随机选择一只布谷鸟i
计算其适应度值Fi
从p中随机选择一个巢穴(假如s)
if(Fi>Fs)
使用新解替换s
end
丢弃一小部分(pa)劣质巢穴,并建立新的巢穴
保留最优解
对解进行排序,找到最优解
每n代同步最优巢穴
end while
end
6.4.6 高斯布谷鸟搜索
基础的布谷鸟搜索虽然可以有效地找到最优解,但是不能保证快速地收敛和精度,为了解决这个问题,Zheng和Zhou(2012)[9]对原始算法引入了一些改进:
σ s = σ o exp ( − μ k ) (19) {\sigma _{\rm{s}}} = {\sigma _{\rm{o}}}\exp ( - \mu {\rm{k}})\tag {19} σs=σoexp(−μk)(19)
其中σ0和µ为常数,k为当前代数。
因此新解通过下式得到:
x i ( t + 1 ) = x i ( t ) + α ⊗ σ s (20) x_i^{(t + 1)} = x_i^{(t)} + \alpha \otimes {\sigma _{\rm{s}}}\tag {20} xi(t+1)=xi(t)+α⊗σs(20)
其中α是与问题规模相关的步长,大多数情况下取1,基于高斯分布的布谷鸟搜索的伪代码如下:
Begin
目标函数f(n),n=(n1,…,nd)T
生成h个巢穴的初始种群ni
while(t<MaxGeneration 或 停止准则)
根据高斯分布随机选择一只布谷鸟
计算其适应度值Fi
从h中随机选择一个巢穴(假如k)
if(Fi>Fk)
使用新解替换k
end
丢弃一小部分(pa)劣质巢穴,并建立新的巢穴
保留最优解
对解进行排序,找到最优解
end while
end
参考文献
- Nayyar, A., D.-N. Le, and N. Nhu, Advances in Swarm Intelligence for Optimizing Problems in Computer Science. 2018, New York: Chapman and Hall/CRC.
- Yang, X. and D. Suash. Cuckoo Search via Lévy flights. in 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC). 2009.
- Yang, X.-S., Cuckoo Search and Firefly Algorithm: Theory and Applications. Vol. 516. 2014.
- Ouaarab, A., B. Ahiod, and X.-S. Yang, Discrete cuckoo search algorithm for the travelling salesman problem. Neural Computing and Applications, 2014. 24(7): p. 1659-1669.
- Ouyang, X., et al., A Novel Discrete Cuckoo Search Algorithm for Spherical Traveling Salesman Problem. Applied Mathematics & Information Sciences, 2013. 7(2): p. 777-784.
- Pereira, L., et al., A Binary Cuckoo Search and Its Application for Feature Selection. 2014. p. 141-154.
- Wang, G.-G., et al., Chaotic cuckoo search. Soft Computing, 2016. 20(9): p. 3349-3362.
- Tzy-Luen, N., Y.T. Keat, and R. Abdullah. Parallel Cuckoo Search algorithm on OpenMP for traveling salesman problem. in 2016 3rd International Conference on Computer and Information Sciences (ICCOINS). 2016.
- Zheng, H. and Y.-Q. Zhou, A novel Cuckoo Search optimization algorithm base on gauss distribution. Journal of Computational Information Systems, 2012. 8: p. 4193-4200.