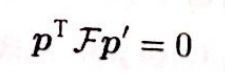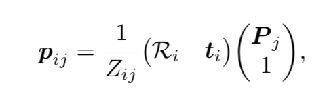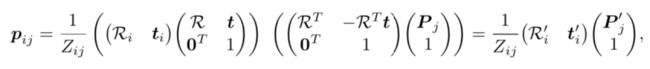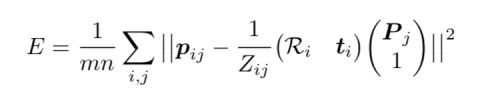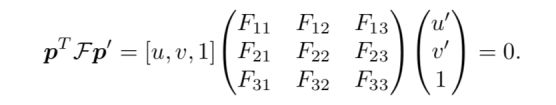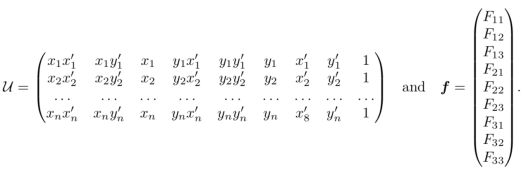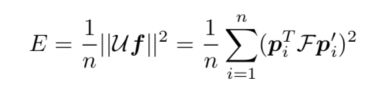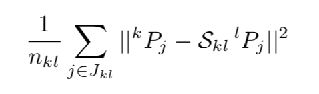低速啃书 计算机视觉：一种现代方法（中文版）第二版 第七八章
第七章 立体视觉 （已经严格标定的摄像机）
获取强烈的深度感:1融合两只眼睛获取的图像 计算对应图像的差别（视差）
设计和实现能模仿人类视觉获取深度的算法（立体感知算法）
应用 ：机器人视觉导航、地图生成、航空勘测和近距照相测量
目标识别的图像分割 计算机图形学的三维场景重建
立体视觉的两个过程：1融合两（多）台摄像机观察到的特征
2重建这些特征的三维图像
单个图像特征的重建易于多个（图7.2）
章节提要：
7.1检验一对摄像机的几何对极约束
7.2关于几何领域的双目重构的算法
7.3人眼的立体视觉原理
7.4基于局部亮度值或边缘模式建立相关线的双目融合算法
7.5近邻像素处将排序和平滑合并在匹配过程中，以联合优化问题的方法求解立体视觉融合
7.6多个摄像头的立体视觉融合
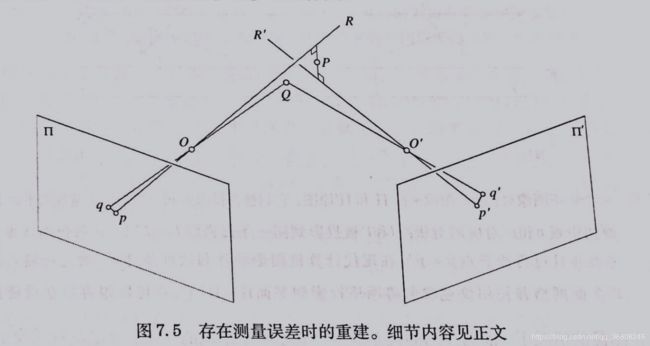
7.1双目计算机的集合属性和对极约束
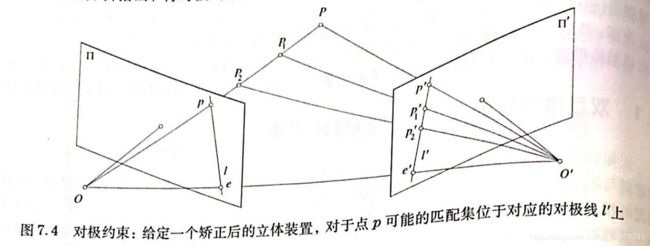
7.1.1对极几何
对于标定过的设备，p的坐标
完全决定连接Op的光线，
决定相关联的对极平面OO'p和对极线l’
结果：对匹配的搜索被限定在对极线l‘上，而非整幅图像。
对于两台摄像机坐标系间的刚性变换未知的情况，对极几何约束了移动的可能范围。
7.1.2 本征矩阵
条件：每台摄像机内部参数已知，图像坐标已经归一化
三个向量共面（一个向量在另外两个向量所在平面）：
本征矩阵是奇异的，并且有两个相等的非0奇异值。
7.1.3基础矩阵
本征矩阵E：包含了物理空间中两个摄像机相关的旋转(R)和平移(T)信息
R和T描述了一台摄像机相对于另外一台摄像机在全局坐标系中的相对位置。
本征矩阵E，是单几何意义上的，与成像仪（摄像机内部）无关，它将左摄像机观测到的点P的物理坐标和右摄像机观测到的相同的点的位置关联起来。
基础矩阵F：除了包含E的信息外，还包含了两个摄像机的内参数。
由于F包含了这些内参数，因此它可以在像素坐标系将两个摄像机关联起来。
基础矩阵F，则是将一台摄像机的像平面上的点在图像坐标系（像素）上的坐标和另一台摄像机的像平面上的点关联起来。
7.2 双目重构
为什么要重构: 在实际中由于标定和特征定位的误差，射线R和R’可能永远也不会真正相交。
方法：建立一条线段同时垂直于R和R‘并与两条射线相交。将线段中心P作为p和p’的原像点
纯代数方法：(易于扩展)
重构场景点的方法：
没有重构点的解析解，通过非线性最小二乘法来估计，可用于多图像。
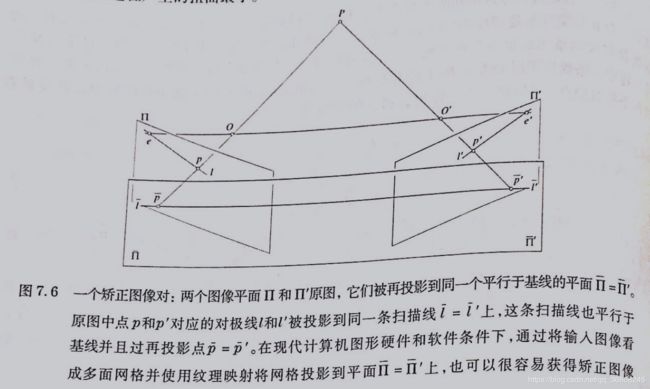
7.2.1 图像矫正
目的：降低立体视觉算法的计算量
方法：通过将原图投影到一个新的图像平面来实现。
在适当的坐标系中（如何选取）矫正图像的对极线和矫正图像的扫描线相同，都平行于基线。
矫正图像平面的选择：1.平面和基线的距离，改变矫正图像的尺度，可以通过图像坐标轴的逆尺度变换来平衡。
2相对于垂直基线的平面，矫正平面的法向量方向（平行于两图像平面交线的一个平面，使投影过程产生的扭曲最小）
视差定义：
7.3 人类立体视觉
简化模型告诉我们：获得场景的绝对位置必须知道聚散角度
但实际上人类神经系统无法准确测量这些角度，但人沿着视线方向上仍可以准确地判断不同物体的深度
人类的双目融合过程不能用直接和实际视网膜相联系的外围过程来解释，起作用的是中枢神经系统和超视网膜。
双目融合算法不重建人类视觉系统模型。
7.4 双目融合的局部算法
仅利用局部信息（附近灰度情况相似的候选点个别像素），建立相关性
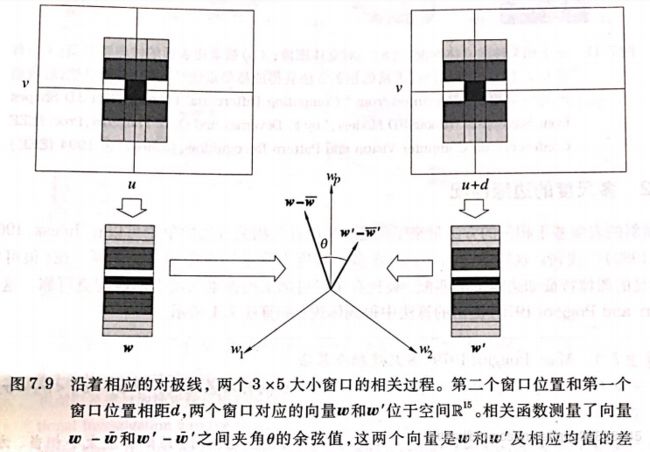
相关方法：
扫描A图数值
定义归一化相关函数
在校正图像对中，假设
(u,v)：第一幅图像中的一个点
w(u,v)：该点对应的向量，是通过扫描窗口每一行数值来获得
(u+d,v)：第二幅图像的匹配点
w'(u+d,v)：该点对应的向量
：代表w的均值
性质：范围【-1，1】
最大值条件：两个窗口亮度值之间的关系形成仿射变换
剪切了大佬的汇报文稿：
计算方法：1最大化转化为最小化：将经过归一化的两个窗口像素值的平方差最小化
2迭代
3绝对误差之和，测试两个灰度模式情况的相差
4用初始估计的视差扭转窗口，补偿透视效果造成的不均衡
利用最优化方法找到合适的视差以及变化率，使两图像间的相关函数达到最大值（图7.10）
7.4.2多尺度的边缘匹配
解决上文观察倾斜表面时，隐含地假设了被观察表面平行于两个图像平面的问题。
第一步：卷积函数：高斯白噪声过程
第三步：滤波器中心为负的部分
第四步：将有大尺度视差的过零点对转移到较小尺度上可以匹配的范围内
5将匹配到的视差存放于缓冲区。用于测试随机点立体图和自然图像
7.5双目融合的全局算法
建模：一个基于近邻像素的序列或者平滑约束的能量函数，对其最小化。
7.5.1排序约束和动态规划
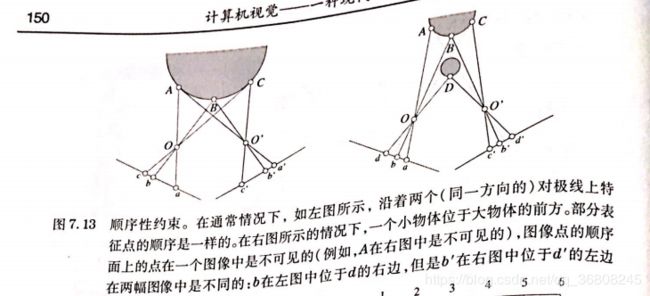
顺序性约束：
不成立条件：小挡大，透明物体
斜线表示灰度匹配，直线表示不匹配，比如上（2，3）间的灰度明显和下（2，3）灰度不同，所以是直线。
问题：在一个图上优化路径代价，节点对应左右图像特征点
目的：最小化关于某离散变量（特征对之间的关联）的误差函数（路径代价）
算法复杂度o（mn）
7.5.2 平滑约束和基于图的组合优化
用依赖约束代替平滑约束（标题为何不是依赖约束？？），最小化基于图定义的能量函数
能量函数：第一项是p邻近像素点的平方差之和
第二项是调整优化，使视差函数尽可能平滑
在子模性约束下具有精确地算法解，然而二元项不能产生子模性问题，采用总先验离差保证视差函数平滑，并不能过惩罚自然关联封闭边界的视差的不连续性。
7.6 使用多台摄像机
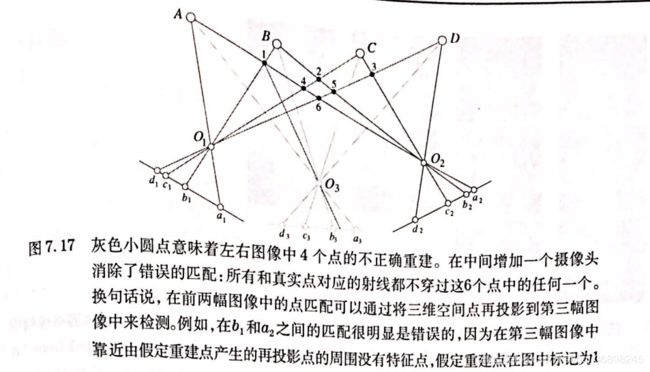
目的：消除大部分由双目图像造成的不确定的匹配点
检测假定匹配：先重构，再投影，无相容，匹配错
另一种：同时利用所有图像来搜索匹配：
假设所有图像都是矫正过的，将搜索正确的视差的操作转换为搜索正确的深度或深度的倒数。
第八章 从运动中恢复结构
SFM：从图像匹配估计匹配点的三维坐标
主要问题：从运动中恢复结构
8.1介绍摄像机为内部标定（内部参数已知）的，它可能用于矫正后的图像坐标情况。
关联透视摄像机的方程
给定某些不确定的旋转矩阵R和平移向量t：
从运动恢复结构问题解决方案被约束为随机相似性，即各向同性正比例的刚性变换。
通过最小化均方误差来估计真实值
8.1.2
关于两个摄像机的透视矩阵的方法，紧接着采用三角测量法重构场景点
输入结构为本征矩阵和基础矩阵，将点的匹配归为估计对极几何问题（弱标定问题）
点集N >= 8的冗余情形
摄像机内参未知—>弱标定输出为基础矩阵F的估计
摄像机内参已知—>本征矩阵ε的估计
未标定的情形下，对极约束
得到n * 9的非齐次线性方程
通过最小化下式得到f（等价于F）
从多幅图像估计欧式结构和运动
最小化
得到相似变换矩阵Skl(3 * 4)
选取随机的基准点，将配准程序应用到其邻接节点，以及邻接节点的邻接节点。该技术并不需要所有点在所有图中显示，只要这个图像构建的图是相互连接的，则可能就是一个完整的重构，场景中的每个点在两幅图中都是可见的。