数据结构-树（赫夫曼树（哈夫曼树）（最优二叉树））-C语言

哈夫曼树（Huffman Tree）是一种特殊的二叉树，这种树的所有叶子节点都带有权值，哈夫曼树的主要目的是产生叶子节点的哈夫曼编码。

哈夫曼树的定义

赫夫曼大叔说，从树中一个结点到另一个结点之间的分支构成两个结点之间的路径，路径上的分支数目称做路径长度。从根结点到各个叶子结点的路径长度与相应结点的权值的乘积的和称为该二叉树的带权路径长度，记作：

如下图所示的带权二叉树：

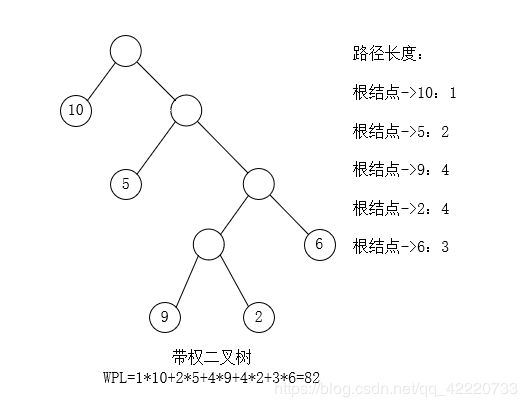
给定一组具有确定权值的叶子结点，可以构造出不同的二叉树，例如用4个整数2、3、5、8作为叶子结点的权值，共可以构造出120棵不同的二叉树，他们的带权路径长度可能不同。其中具有最小带权路径长度的二叉树称为哈夫曼树。

构造哈夫曼树

根据哈夫曼树的定义，一棵二叉树要使其WPL值最小，必须使权值大的叶子结点更靠近根结点，而权值小的叶子结点更远离根结点。
以下图都是以权值代替结点，构造大致步骤图示如下：
第一步：确定所有的叶子结点权值。

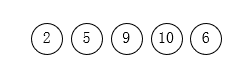
第二步：选择叶子结点权值最小的两个结点2和5作为一个新结点7的孩子结点。注意：权值相对较小的为新结点的左孩子，反之为右孩子，新节点权值=左右孩子权值之和。

第三步：将之前操作过的结点划去、新结点加入。

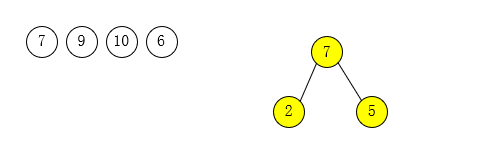
第四步：选择叶子结点权值最小的两个结点6和7作为一个新结点13的孩子结点。

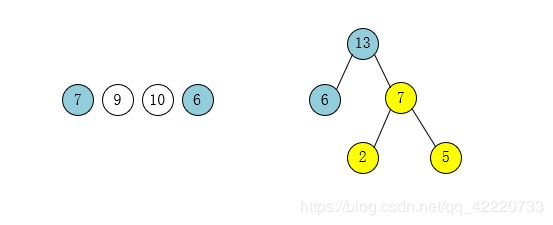
第五步：将之前操作过的结点划去、新结点加入。

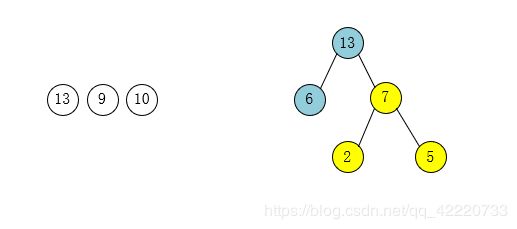
第六步：选择叶子结点权值最小的两个结点9和10作为一个新结点19的孩子结点。

第七步：将之前操作过的结点划去、新结点加入。

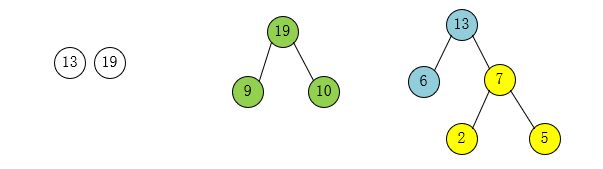
第八步：选择叶子结点权值最小的两个结点13和19作为一个新结点32的孩子结点。

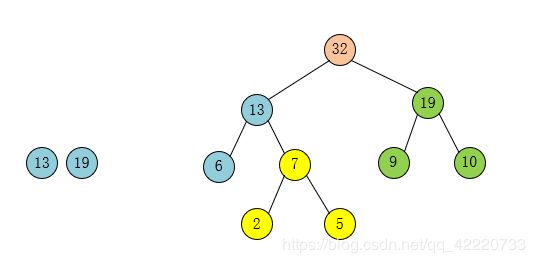
第九步：将之前操作过的结点划去、完成哈夫曼树的创建

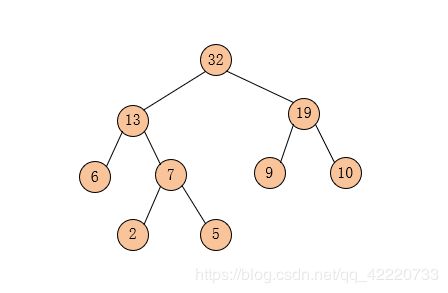
哈夫曼树编码

哈夫曼树编码具有广泛的应用，最开始它的目的是为了解决当年远距离通信(主要是电报)的数据传输的最优化问题,至于为什么可以做优化可以上百度或谷歌自行学习，我这里只是说说怎么用0和1做编码。
假设字母A,B,C,D,E这5个字符出现频率分别是0.1875,0.0625,0.15625，0.28125,0.3125。

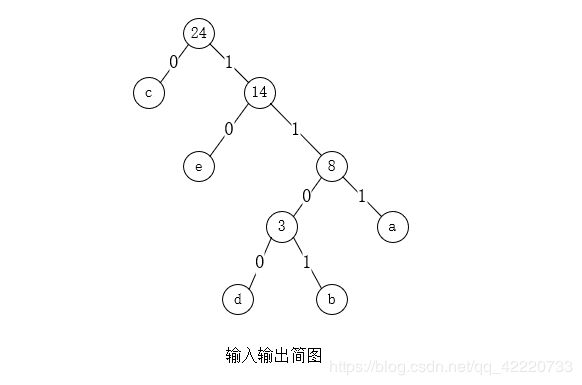
我们将权值放大一些（这里是我偷懒没有修改数值，大家要注意的是这里的权值是各个字符出现的频率）并将权值的左分支规划为0，右分支规划为1，则出现下图所示内容。

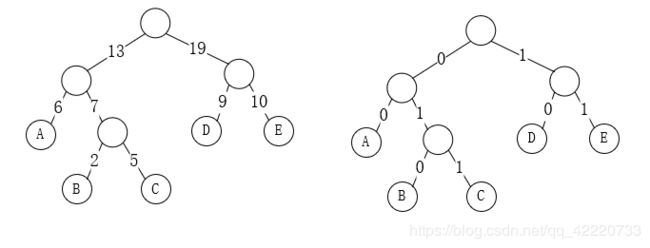
取每条路径上的0和1的序列作为各个叶子 结点对应的字符编码，这就是哈夫曼编码。

从哈夫曼编码可以看出，对于n个字符，构造他们的哈夫曼编码，没有一个字符的哈夫曼编码是另一个字符的哈弗曼编码的前缀，如某个字符的哈弗曼编码为11，则该字符组中不可能出现以11开头的哈弗曼编码了。而且对于每个字符对应的哈夫曼编码中0、1个数m是小于所有字符总数n的。

相关代码

//二叉树 - 哈夫曼树
#include 
#include 
#define n 5			//叶子数目 
#define m n*2-1		//构造哈夫曼树的结点数 
#define maxnum 100.0   //代指float的最大数 
#define maxsize 20   //char数组最大空间 
#define error 0
#define ok 1	
typedef int bool;	
typedef char datatype; 
typedef char String[maxsize]; 
typedef struct
{
	datatype data;				//该结点的字符 
	float weight;					//该结点对应权值 
	int lchild,rchild,parent;	//左右孩子及双亲的下标 
}hfmtree;//哈夫曼树 
typedef struct
{
 char bits[n];   //存放编码 
 int start;      //每个字符的编码在bit中的起始位置
 datatype data;    //对应的字符
}codetype;//哈夫曼编码

void hufman(hfmtree tree[]);
void print_tree(hfmtree tree[],int t);
void hufmancode(hfmtree tree[],codetype code[]);
void print_hufmancode(codetype code[]);
bool decode(hfmtree tree[]);

int main()
{
	hfmtree tree[m];
	codetype code[n]; 
	int i,j;

	hufman(tree); 
	hufmancode(tree,code);
	  
	printf("正序输出哈夫曼树(多余结点使用'@'代替)：\n");
	print_tree(tree,m-1);
	printf("\n");
	
	printf("输出哈夫曼编码：\n");
	print_hufmancode(code);
	printf("\n");
	
	printf("通过哈夫曼树进行解码：\n");
	decode(tree);
	printf("\n");
}
//对一串编码字符通过哈夫曼树进行解码 
bool decode(hfmtree tree[])
{
	String str;
	int i,j=0;
	i=m-1;	//根结点下标 
	
	printf("请输入编码字符串：\n");
	gets(str);
	printf("译码字符：\n ");
	while(str[j]!='\0')
	{
		if(str[j]=='0')
			i=tree[i].lchild;
		else if(str[j]=='1')	
			i=tree[i].rchild;
		else
			return error;
		if(tree[i].lchild==-1 && tree[i].rchild==-1)     //访问到叶子结点 
		{
			printf("%c",tree[i].data);
			i=m-1;     	
		}
		j++;
	} 
	if(tree[i].data=='@') 
		return error;
	return ok;
}
//创建哈夫曼树 
void hufman(hfmtree tree[])
{
	//p1,p2为最小权和次小权值对应哈夫曼树结点的下标 
	//max_1,max_2为最小权和次小权值
	int i,j,p1,p2;
	float f,max_1,max_2;
	datatype c;
	 
	for(i=0;i<m;i++)    //初始化
	{
	tree[i].parent=-1;
	tree[i].lchild=-1;
	tree[i].rchild=-1;
	tree[i].weight=0.0;
	}
	printf("Input data and weight:\n");
	for(i=0;i<n;i++)  	//读入前n个结点的字符及权值
	{
	scanf("%c,%f",&c,&f);
	getchar();			//用以吸收回车键 
	tree[i].data=c;
	tree[i].weight=f;
	}
	for(i=n;i<m;i++)    //进行n-1次合并重组，产生n-1个新结点
	{
		//每次重组都需将变量刷新，否则只保留第一次比较过后的数值 
		max_1=max_2=maxnum;
		p1=p2=-1;
		for(j=0;j<i;j++)//取最小权值、次小权值及对应结点坐标 
			if(tree[j].parent==-1)
				if(tree[j].weight<max_1)	 //最小 
				{
					max_2=max_1;
					max_1=tree[j].weight;
					p2=p1;
					p1=j;
				}else if(tree[j].weight<max_2)//次小 
					{
						max_2=tree[j].weight;
						p2=j;
					}
		tree[i].lchild=p1;
		tree[i].rchild=p2;
		tree[i].parent=-1;
		tree[i].data='@';	
		tree[p2].parent=i;
		tree[p1].parent=i;
		tree[i].weight=tree[p2].weight+tree[p1].weight;
	} 
}
//正序输出哈夫曼树 
void print_tree(hfmtree tree[],int t)
{
	if(t!=-1)
	{
		printf("%3c",tree[t].data);
		print_tree(tree,tree[t].lchild);
		print_tree(tree,tree[t].rchild);		
	}
} 
///根据哈夫曼树求出哈夫曼编码
void hufmancode(hfmtree tree[],codetype code[])
{
	int i,p,x;

	//有n个字符及对应的编码 
	for(i=0;i<n;i++)
	{
		code[i].data=tree[i].data;
		code[i].start=n;			//在bits数组中从后至前添加数据 
		x=i;
		p=tree[i].parent;
		while(p!=-1)//利用双亲回溯 
		{
			code[i].start--;
			if(tree[p].lchild==x)
				code[i].bits[code[i].start]='0';
			else
				code[i].bits[code[i].start]='1';
			x=p;
			p=tree[p].parent;
		}
	}
}
//输出哈夫曼编码 
void print_hufmancode(codetype code[])
{
	int i,j;
	for(i=0;i<n;i++)
	{
		printf("%c--->",code[i].data);
		for(j=code[i].start;j<n;j++)
		{
			printf("%c",code[i].bits[j]);
		}
		printf("\n");
	}
}

结果图示

不足之处，还请批评指正。