算法题目（python代码）——给定二叉查找树结构和序列元素，用序列元素来填充BST

Problem

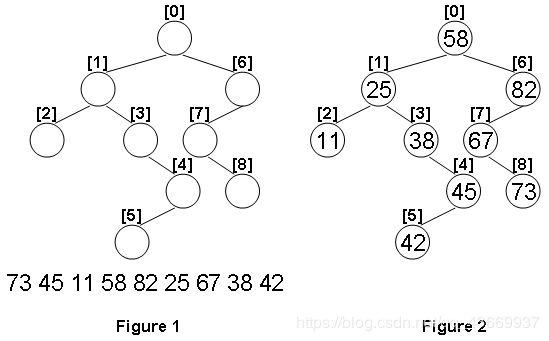
给定一个二叉树结构，与一个整数列表，请将整数填充至二叉树对应节点内，使其成为一个二叉查找树；请输出该二叉查找树的层次遍历。下图展示了给定样例对应的二叉树结构：

需要通过用户输入的方式，生成二叉树结构。比如：

1 6
2 3
-1 -1
-1 4
5 -1
-1 -1
7 -1
-1 8
-1 -1

用户输入N行分别给定了编号由0至(N-1)的节点的左右子树编号，以空格分隔；若编号-1则代表对应子树为空。结合figure 1来理解二叉树的生成算法。编号只是每个节点的唯一标识。然后给定同样元素数量的序列，需要填充到给定的树结构中，就像figure 2。

Solution

思路来自于AVL树的平衡因子，二叉查找树具有“左小右大”的性质，具有一定的次序，AVL树关注的是树结构的平衡，才要计算每个节点的左右树高度差，但是对于填充二叉树来说，更关心的是怎么从序列中找到节点，所以在生成树的过程中就要计算每个节点左右树的节点数量差(以下简称diff)。结合左右树的节点数量差，从有序表的中间元素开始找节点元素。

Define the binary search tree

class FixedTree:
    def __init__(self,number,parent=None):
        self.number = number
        self.value = None
        self.left = None
        self.right = None
        self.parent = parent # 父节点指针，用于更新节点数量差
        self.l = 0 # 左子树的节点数量
        self.r = 0 # 右子树的节点数量
    def diff(self):
        return self.l - self.r
     # 判断左子树还是右子树
    def isleft(self):
        return self.parent.left == self
    def isright(self):
        return self.parent.right == self

Update the difference of left and right tree number

def updateDiff(node):
        parent = node.parent
        # 每当有新节点插入树中，都要更新其所有父节点的左右节点数量
        while parent:
            # 空节点不算
            if node.number == "-1":
                break
            if node.isleft():
                parent.l +=1

            else:
                parent.r +=1
            node = node.parent
            parent = parent.parent

Generate the BST

def generateTree(total):
    TreeStack = []
    count = 0
    root = FixedTree("0")
    r = root
    for i in range(total):
        count+=1
        string = input("please input the left and right tree! this{}tree".format(count))
        ls = string.split(" ")
        r.left = FixedTree(ls[0],r)
        updateDiff(r.left)
        r.right = FixedTree(ls[1],r)
        updateDiff(r.right) # 更新所有父节点的diff参数
        # 都为-1时，需要依赖栈来跳转节点,没有插入新节点
        if ls[0] == "-1" and ls[1] == "-1":
            try:
                r = TreeStack.pop() # 由于之前队列弹出了元素做root，所以被压入队列的一定是个单元素的列表
            except IndexError:
                pass
        elif ls[0] == "-1"or ls[1] == "-1":
            # 两父子节点的指针互换才能实现树的完整链接
            if ls[1] == "-1":
                r = r.left
            else:
                r = r.right
        # 当树两边都命名的时候
        else:
            # 用栈来存储待插入数据的节点，也就是右子树
            TreeStack.append(r.right)
            r = r.left
    return root

Fill the BST with python list

def fillTree(numList,r):
    ls = sorted(numList) # 充分利用二叉查找树的特性，通过计算每个节点左右节点数量差，来判断哪个元素做节点
    tq = [] # 装树的队列
    lq = [] # 装列表的队列
    root = r
    tq.append(root)
    # 层级遍历BST且每次从有序列表的中间元素开始找，结合每个元素已计算好的左右节点数量差（diff）来找节点元素
    while True:
        index = len(ls)// 2
        root = tq.pop(0)
        print(root.number,ls)
        # diff为0 就是叶节点。
        if root.diff == 0 or index==0:
            root.value = ls[0]
            
        # 加减1 还不太严谨
        elif root.diff()>=1 and root.diff()<=2:
        # 列表元素数量大于2时，就可以从节点元素开始，列表切片划分左子树和右子树的元素
            if len(ls)>2:
                root.value = ls[index+1]
                lq.append(ls[:index+1])
                lq.append(ls[index+2:])
        # 列表元素较少时就直接从中弹出元素
            else:
                root.value = ls.pop(1)
                lq.append(ls)
        elif root.diff()<=-1 and root.diff() >=-2:
            if len(ls)>2:
                root.value = ls[index-1]
                lq.append(ls[:index-1])
                lq.append(ls[index:])
            else:
                root.value = ls.pop(0)
                lq.append(ls)
         
        # 要避免空节点进入队列参与计算
        if root.left != None and root.left.number != "-1":
            tq.append(root.left)
        
        if root.right != None and root.right.number != "-1":
            tq.append(root.right)
        
        # 切片难免会产生空列表，用循环来弹出空列表
        while True:
            if lq != []:
                ls = lq.pop(0)
            if ls != []:
                break
    # 所有节点都填充好了就退出循环
        if len(tq) == 0:
            break  
    return r

不过具体在找节点元素时，做得不够严谨，因为笔者用样例([73,45,11,58,82,25,67,38,42])试了下，发现所有节点diff都在-1 ~ 2 之间，所以从中间元素索引加减1就能正确找到节点元素了，但不具有普适性，各位大佬有什么更好的做法也欢迎分享一下。

最后一次调用各个方法就好了

ft = generateTree(9)
fillTree([73,45,11,58,82,25,67,38,42],ft)

不信就写个遍历算法试试看