图像分割—学习笔记

图像分割（segmentation）是将数字图像细分为多个图像子区域（像素的集合）（也被称作超像素）的过程，就是把图像分成若干个特定的、具有独特性质的区域并提出感兴趣目标的技术和过程。它是由图像处理到图像分析的关键步骤。图像分割的目的是简化或改变图像的表示形式，使得图像更容易理解和分析。图像分割通常用于定位图像中的物体和边界（线、曲线等）。更精确的，图像分割是对图像中的每个像素加标签的一个过程，这一过程使得具有相同标签的像素具有某种共同视觉特性。
图像分割的结果是图像上子区域的集合（这些子区域的全体覆盖了整个图像），或是从图像中提取的轮廓线的集合（例如边缘检测）。一个子区域中的每个像素在某种特性的度量下或是由计算得出的特性都是相似的，例如颜色、亮度、纹理。邻接区域在某种特性的度量下有很大的不同。

基于阈值的分割方法

基于图像的灰度特征来计算一个或多个灰度阈值，并将图像中每个像素的灰度值与阈值相比较，根据比较结果把像素分到合适的类别中。该类方法的关键是按照某个准则函数来求解最佳灰度阈值。

Otsu阈值分割

Otsu（大津法或最大类间方差法）使用的是聚类的思想，把图像的灰度数按灰度级分成2个部分，使得两个部分之间的灰度值差异最大，每个部分之间的灰度差异最小，通过方差的计算来寻找一个合适的灰度级别来划分。所以可以在二值化的时候采用ostsu算法来自动选取阈值进行二值化。Otsu算法被认为是图像分割中阈值选取的最佳算法，计算简单，不受图像亮度和对比度的影响。因此，使类间方差最大的分割意味着错分概率最小。

自适应阈值分割

最大熵阈值分割法

迭代阈值分割

基于边缘的分割方法

边缘是图像中两个不同区域的边界线上连续的像素点的集合，是图像局部特征不连续性的反映，体现了灰度、颜色、纹理等图像特性的突变。基于边缘的分割方法是基于灰度值的边缘检测，建立在边缘灰度值会呈现出阶跃型或屋顶型变化这一观测基础上的方法。阶跃型边缘两边像素点的灰度值存在着明显的差异，而屋顶型边缘则位于灰度值上升或下降的转折处。可以使用微分算子进行边缘检测，使用一阶导数的极值与二阶导数的过零点来确定边缘，具体实现可以使用图像与模板进行卷积来完成。

基于区域的分割方法

按照图像相似性准则分成不同的区域，主要 包括种子区域生长法、区域分裂合并法和分水岭法等几种类型。
种子区域生长法是从一组代表 不同生长区域的种子像素开始，将种子像素邻域里符合条件的像素合并到种子像素所代表的生长区域中，并将新添加的像素作为新的种子像素继续合并过程，直到找到符合条件的新像素为止。该方法的关键是选择合适的初始种子像素以及合理的生长准则。
区域分裂合并法的基本思想是首先将图像任意分成若干互不相交的区域，然后再按照相关准则对这些区域进行分裂或者合并从而完成分割任务。该方法既适用于灰度图像分割也适用于纹理图像分割。
分水岭法是一种基于拓扑理论的数学形态学的分割方法，其基本思想是把图像看作是测地学上的拓扑地貌，图像中每一点像素的灰度值表示该点的海拔高度，每一个局部极小值及其影响区域称为集水盆，而集水盆的边界则形成分水岭。该算法的实现可以模拟成洪水淹没的过程，图像的最低点首先被淹没，然后水逐渐淹没整个山谷。当水位到达一定高度的时候将会溢出，这时在水溢出的地方修建堤坝，重复这个过程直到整个图像上的点全部被淹没，这时所建立的一系列堤坝就成为分开各个盆地的分水岭。分水岭算法对微弱的边缘有着良好的响应，但图像中的噪声会使分水岭算法产生过分割的现象。

基于图论的分割方法

把图像分割问题与图的最小分割问题相关联。首先将图像映射为带权无向图$G=<V,E>$，图中每个节点$N\in V$对应于图像中的每个像素，每条边$\in E$连接着一对相邻的像素，边的权值表示了相邻像素之间在灰度、颜色或纹理方面的非负相似度。对图像的一个分割$S$就对应图的一个剪切，被分割的每个区域$C\in S$对应这图中的一个子图。而分割的最优原则就是使划分后的子图在内部保持相似度最大，而子图之间的相似度保持最小。基于图论的分割方法的本质就是移除特定的边，将图划分为若干子图从而实现分割。基于图论的方法有GraphCut、GrabCut和Random Walk等。

基于聚类的分割方法

初始化一个聚类，使用迭代的方式将颜色、亮度、纹理等特征相似的像素点聚类到同一超像素，迭代直至收敛，从而得到最终的图像分割结果。基于像素聚类的代表方法有K-menas（K均值）、谱聚类、Meanshift和SLIC等。

基于能量泛函的分割方法

基于能量泛函的分割方法主要指的是活动轮廓模型（active contour model）以及在其基础上发展出来的算法，其基本思想是使用连续曲线来表达目标边缘，并定义一个能量泛函使得其自变量包括边缘曲线，因此分割过程就转变为求解能量泛函的最小值的过程，一般可通过求解函数对应的欧拉（Euler.Lagrange）方程来实现，能量达到最小时的曲线位置就是目标的轮廓所在。
主动轮廓线模型是一个自顶向下定位图像特征的机制，通过事先在感兴趣目标附近放置一个初始轮廓线，在内部能量（内力）和外部能量（外力）的作用下变形，外部能量吸引活动轮廓朝物体边缘运动，而内部能量保持活动轮廓的光滑性和拓扑性，当能量达到最小时，活动轮廓收敛到所要检测的物体边缘。
按照模型中曲线表达形式的不同，活动轮廓模型可以分为两大类：参数活动轮廓模型（parametric active contour model）和几何活动轮廓模型（geometric active contour model）。
参数活动轮廓模型是基于lagrange框架，直接以曲线的参数化形式来表达曲线，如snake模型，该类模型分割结果受初始轮廓的设置影响较大，难以处理曲线拓扑结构变化等缺点，此外其能量泛函只依赖于曲线参数的选择，与物体的几何形状无关。
几何活动轮廓模型的曲线运动过程是基于曲线的几何度量参数而非曲线的表达参数，因此可以较好的处理拓扑结构的变化，如水平集方法。

曲线演化理论

曲线存在曲率，曲率有正负，在法向曲率力的推动下，曲线的运动方向之间有所不同：有些部分朝外扩展，而有些部分朝内运动。简单曲线在曲率力（也就是曲线的二次导数）的驱动下演化所具有的一种非常特殊的数学性质：一切简单曲线，无论被扭曲的多么严重，只要还是一种简单曲线，那么在曲率力的推动下最终将退化成一个圆，然后消逝（圆的所有点的曲率力都向着圆心，所以它将慢慢缩小，以致最后消逝）。
描述曲线几何特征的两个重要参数是单位法向量和曲率，单位法向量描述曲线的方向，曲率则表述曲线弯曲的程度。曲线演化理论就是利用曲线的单位法向量和曲率等几何参数来研究曲线随时间的变形。曲线的演变过程可以认为是表述曲线在作用力$F$的驱动下，朝法向量方向$N$以速度$v$演化。如果速度$v$为负，表示活动轮廓演化过程是朝外部方向的，如果为正，则表示朝内部方向演化，活动曲线是单方向演化的，不可能同时往两个方向演化。
所以曲线的演变过程，就是不同力在曲线上的作用过程，力也可以表达为能量。世界万物都趋向于能量最小而存在。在图像分割里面，在目标轮廓这个地方，整个轮廓的能量是最小的，那么曲线在图像任何一个地方，都可以因为力朝着这个能量最小的轮廓演变，当演变到目标轮廓的时候，因为能量最小，力平衡了，速度为0了，也就不动了，这时候目标就被分割出来了。

snake方法

snake方法是基于能量泛函的方法，核心思想就是，在感兴趣区域的附近给出一条初始曲线，在曲线固有内力（控制曲线的弯曲和拉伸）和图像外力（控制收敛到局部特征）的作用下收敛到目标的边界轮廓。但是snake方法需要将曲线进行参数化，这是个非常困难的问题，而且它还不能处理曲线的拓扑变换。
简单的来讲，snake模型就是一条可变形的参数曲线及相应的能量函数，以最小化能量目标函数为目标，控制参数曲线变形，具有最小能量的闭合曲线就是目标轮廓。
构造snake模型是为了调和上层知识和底层图像特征这一矛盾。无论是亮度、梯度、角点、纹理还是光流，所有的图像特征都是局部的。所谓局部性就是指图像上某一点的特征只取决于这一点所在的邻域，而与物体的形状无关。但是人们对物体的认识主要是来自于其外形轮廓。如何将两者有效的融合在一起是snake模型的长处。snake模型的轮廓线承载了上层知识，而轮廓线与图像的匹配又融合了底层特征。这两项分别表示为snake模型中能量函数的内部力和图像力。
模型的形变受到同时作用在模型上的许多不同的力所控制，每一种力所产生一部分能量，这部分能量表示为活动轮廓模型的能量函数的一个独立的能量项。

水平集(LevelSet)

用Level Set来表示Snakes，想法很简单：一个平面上的曲线可以表示成一个二元函数$z=f(x,y)$的零点集合（Zero Level Set），集这个二元函数$z=f(x,y)$所表示的三维曲面与$xy$平面的交线。更一般的，任何$N$维曲面都可以表示为一个$N+1$维曲面与一个$N$维超平面的交集，或称为$N+1$维曲面在$N$维超平面上的投影。相对最早的Snake（用参数化的曲线，所以也叫parametric active contour），用level set表示的活动曲线叫Geometric Active Contours。

用二维曲面与二维平面的交线表示曲线，当描述曲线运动的时候，用level set表示曲线就有很明显的优势，例如：几条曲线在运动中merge成一条曲线，或者一条曲线分裂成几条曲线，这样的拓扑变化是不可能表示成一条连续的参数化曲线的运动。原因很简单，一条连续的参数化曲线是用一个一元连续函数来表示的，它显然不能表示几条分开的曲线（这与连续性矛盾）。

水平集（LevelSet）是一种基于能量泛函的图像分割算法，即把图像分割的问题，转换为最小化一个能量函数的问题。主要应用于医学图像分割。
水平集算法的核心思想是将要研究的问题，看做是更高一维空间的函数（也就是水平集函数）的零水平集。因此，研究某一曲线（曲面）的演化过程，实际上就等于研究更高一维曲面的演化过程。

如上图所示，对红色曲线建立一个随时间而变换的模型，是很困难的，因为发生了拓扑结构变化（一条曲线变成了两条），但是如果只是对蓝色的曲面建立随时间变化的过程，则是可行的，而红色曲线就是取其$Z=0$的水平集。这就是隐函数的思想，当无法显示写出x为自变量的函数 y，但是可以得到y和x的某种关系时，就能通过另外一种方法来表达。

假设曲线为$C$，它是随时间变化的，那么曲面（也就是水平集函数）的描述式如下：
$$\phi (C(t),t)=0$$
偏微分求解后就是一个如下的式子：
$$\frac{\partial \phi }{\partial t}=F|▽\phi |$$
给$\phi$一个初始值，它就可以在$F$的作用下进行演化，然后令其等于0，就得到了$C$。所以最关键的问题是求取$F$，也就是演化函数，这就是水平集方法的核心思想。

Active Contours Without Edges

• paper
  Active Contours Without Edges
• translation
  无边界活动轮廓模型
• code
  morphasnakes

Active Contours Without Edges是一种基于曲线演化，Mumford-Shah函数和水平集的新的活动轮廓模型来检测图像中的目标。无论边界是否由梯度定义，模型均可检测目标。最小化能量函数可以作为最小化问题的一种特例。在水平集方程中，最小化问题则变为平均曲率流问题，就像活动轮廓的演化一样，可以在所需要的边界停止演化。但是停止的条件不像经典的活动轮廓模型一样依赖与图像的梯度，而是与相关的分割参数有关。

能量函数

• $\Omega$：$R^2$中的有界开子集
• $u_0$：从$\Omega \to R$的映射，表示图片
• $C(s)$：从$[0,1]\to R^2$的映射，表示曲线
• $\omega$：$\Omega$中的开集，曲线$C$是其边界，即$C=\partial \omega$

假定给定一张特殊图片$u_0$，这张图片由两块区域构成，区域一所有的像素点取值都为$u_0^i$，区域二中所有的像素点取值都为$u_0^o$。现在希望得到区域一的轮廓。考虑控制着曲线最终拟合至物体边缘停止的fitting项。
$$F(C)={\int }_{inside(C)}|u_0(x,y)-c_1{|}^{2}dxdy+{\int }_{outside(C)}|u_0(x,y)-c_2{|}^{2dxdy}$$
其中常数$c_1$和$c_2$分别是曲线$C$内部像素点的均值和$C$外部像素点的均值。对于该特殊图片$u_0$，使得这个能量函数值最小的曲线$C$就是希望得到的区域一的轮廓，此时能量值为0（可以验证曲线$C$不是区域一轮廓的其他几种情况，对应的能量值都大于0）。作者提出的模型就是上面的能量函数，另外还加上了曲线的长度、曲线的内区域的面积等正则项：
$$\begin{array}{rl}F(C)=\mu \cdot Length(C)+\nu \cdot Area(inside(C))& +{\lambda }_1{\int }_{inside(C)}|u_0(x,y)-c_1{|}^{2}dxdy\\ & +{\lambda }_2{\int }_{outside(C)}|u_0(x,y)-c_2{|}^{2}dxdy\end{array}$$
其中，$\mu \ge 0$， $\nu \ge 0$，${\lambda }_1,{\lambda }_2\ge 0$。因为$c_1$和$c_2$也是$C$的函数，所以$F(c_1,c_2,C)$即$F(C)$。

能量函数是Mumford-Shah的特例，因为Mumford-Shah有极小值，所以能量函数也有极小值。

用水平集函数表示曲线

为了求解能量函数的极小值问题，作者把关于曲线$C$的能量函数写成关于水平集函数$\varphi$的能量函数（函数的函数—泛函），求解水平集函数。
要用$\varphi$替换能量函数中的曲线$C$，需要引入两个函数，简称为$H$函数和$Delta$函数：
$$H(z)=\{\begin{array}{ll}1,& z\ge 0\\ 0,& z<0\end{array}$$

$${\delta }_0(z)=\frac{d}{dz}H(z)$$

能量公式重新写成：
$$\begin{array}{rl}F(c_1,c_2,\varphi )=\mu {\int }_{\Omega }\delta (\varphi (x,y))|▽\varphi (x,y)|dxdy& +\nu {\int }_{\Omega }H(\varphi (x,y))dxdy\\ & +{\lambda }_1\int |u_0(x,y)-c_1{|}^{2}H(\varphi (x,y))dxdy\\ & +{\lambda }_1\int |u_0(x,y)-c_2{|}^2(1-H(\varphi (x,y)))dxdy\end{array}$$

$c_1$和 $c_2$通过$\varphi$求出：
$$\{\begin{array}{l}{c}_1=average(u_0)in\{\varphi \ge 0\}\\ c_2=average(u_0)in\{\varphi <0\}\end{array}$$

变分法得到欧拉-拉格朗日公式

针对泛函极值问题，可以得到$\varphi$的欧拉-拉格朗日公式，即一个偏微分方程：
$$\frac{\partial \varphi }{\partial t}={\delta }_{ϵ}(\varphi )[\mu \cdot div(\frac{▽\varphi }{|▽\varphi |})-\nu -{\lambda }_1(u_0-c_1{)}^2+{\lambda }_2(u_0-c_2{)}^2]=0$$

$$\varphi (0,x,y)={\varphi }_0(x,y)in\Omega$$

$$\frac{{\delta }_{ϵ}(\varphi )}{|▽\varphi |}\frac{\partial \varphi }{\partial n}=0on\partial \Omega$$

其中，$n$是边界$\partial \Omega$的外法线。因为原来的$\partial {\delta }_0$基本上处处为0，没办法求欧拉-拉格朗日方程，所以在得到的欧拉-拉格朗日方程中并没有使用上面的$H$函数以及对应的$Delta$函数，而使用下面的函数，现在$\partial {\delta }_{\in }$的支撑集是整个实数集$R$，所以不管初始曲线是什么样的，都可以得到全局最优解，还可以检测到内部的轮廓。
$$H_{ϵ}=\frac{1}{2}(1+\frac{2}{\pi }arctan(\frac{z}{ϵ}))$$

$${\delta }_{ϵ}=H_{{ϵ}^{{}^{\prime }}}=\frac{ϵ}{\pi }\frac{1}{z^2+{ϵ}^2}$$

当$ϵ\to 0$时，分别收敛到$H$和${\delta }_0$。

迭代法解偏微分方程

经过对偏微分方程离散化，得到水平集函数$\varphi$的迭代形式：
$$\frac{{\varphi }_{i,j}^{n+1}-{\varphi }_{i,j}^n}{△t}={\delta }_h({\varphi }_{i,j}^n)[\mu curvatur{e}_{i,j}-\nu -{\lambda }_1(u_{0,i,j}-c_1{)}^2+{\lambda }_2(u_{0,i,j}-c_2{)}^2]$$

算法步骤

（1）随机初始化${\varphi }^0={\varphi }_0$， $n=0$
（2） 计算两个均值$c_1$和$c_2$
（3）根据迭代公式计算${\varphi }^{n+1}$
（4） 重新初始化$\varphi$，这一步可用可以不用
（5）检查是否收敛，收敛则停止，否则跳到步骤（2），直到收敛停止

基于深度学习的分割方法

在实际场景的图片中，一些物体的结构比较复杂，内部差异性较大，仅利用像素点的颜色、亮度、纹理等较低层次的内容信息不足以生成好的分割效果，容易产生错误的分割。因此需要更多的结合图像提供的中高层内容信息辅助图像分割。
根据实际分割应用任务的不同，可以分为三个研究方向：语义分割、实例分割、全景分割。

• 语义分割
  像素级别的语义分割，对图像中的每个像素都划分出对应的类别，集实现像素级别的分类。
• 实例分割
  类的具体对象即为实例，实例分割不仅要进行像素级别的分类，还需要在具体的类别基础上区别开不同的实例。
• 全景分割
  全景分割是语义分割和实例分割的泛化，与语义分割不同，全景分割需要区分单个目标实例，与实例分割不同的是，在全景分割中目标分割中必须是非重叠的。

Unsupervised Image Segmentation by Backpropagation

• paper
  UNSUPERVISED IMAGE SEGMENTATION BY BACKPROPAGATION
• code
  pytorch-unsupervised-segmentation
  Unsupervised-Segmentation
  聚类预测的三个准则：
  • 具有相似特征的像素点期望分配相同的标签（使用线性分类器）
  • 空间连续的像素期望分配相同的标签（强制每个超像素中的所有像素具有相同的聚类标签）
  • 每类标签集期望足够大（批量标准化处理）

算法理解：

• 使用经典的机器学习算法，为输入图片进行预分类，调整算法参数，为语义信息明显相同的小区域分配相同的语义标签。因为具有相同语义的像素在图像中的连续区域内。所以颜色接近、纹理接近且位置接近的像素可以为其分配相同的语义标签。
• 使用深度学习结合自动编码器结构，对输入图像进行分类，使输出的语义分割结果尽可能的符合预分类的结果，训练到收敛。
• 深度学习的语义分割结果会在符合预分类结果的基础上，将具备相同语义信息的小区块进行合并，得到大区块。
• 深度学习（神经网络）在整个无监督语义分割任务中，承担的任务是：对经典机器学习无监督语义分割的细粒度预分类结果进行处理。并在迭代中，逐步对小区块进行合并，最后得到符合人类预期的语义分割结果。

算法缺点：

• 随着迭代，算法会逐步被合并各个分区。但是算法里却没有设定限制，去抑制神经网络对小区域的合并。
• 设计的损失函数，无法对神经网络输出一张仅含有一个类别的结果进行限制，因此神经网络的参数要足够小，这样的设计容易过拟合。

scikit-image图像分割模块

SCIKit Image是一个专门用于图像处理的Python包。

安装

pip install scikit-image

图像导入

• 从skimage库导入灰度/彩色图像
  skimage数据模块包含一些内置示例数据集。

from skimage import data
# 灰度图像
image = data.bianry_blobs()
#彩色图像
image = data.astronaut()

• 从外部导入图像
  导入图像模块为I/O模块。

from skimage import io
#单张图像
image = io.imread('skimage_logo.png')
#多张图像
images  = io.ImageCollection('../images/*.png:../images/*.jpg')
# 读取图像数量
print(len(images))
#显示第一张图像
io.imshow(images[0])
#保存图像
io.imsave('logo.png', images[0])

图像分割

图像分割本质上是将数字图像分割成多个片段的过程，以简化或将图像的表示方式更改为更有意义和更易于分析的内容。

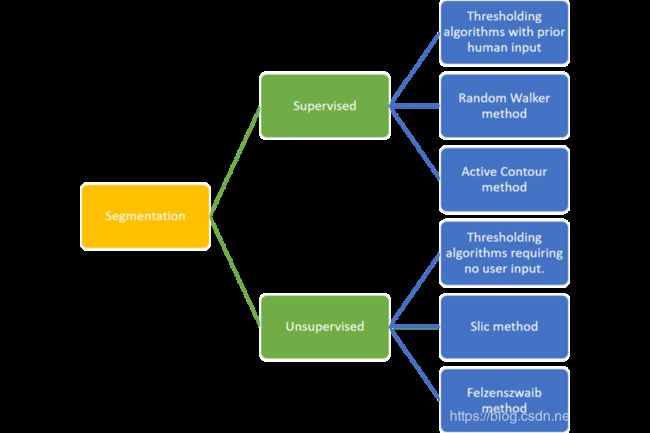
阈值法分割图像

• 有监督阈值：阈值是人工手动选择的。
• 无监督阈值：在选择最佳阈值时不需要手动输入（如otsu）。

阈值分割是一种非常基本的分割算法，但是它在高对比图像中效果不是很好，需要采用更加先进的算法。

• 监督分割算法：一些可能来自人类输入的先验知识被用来知道算法。
  • 活动轮廓分割（Active Contour segmentation）：活动轮廓分割使用用户定义的轮廓或线在感兴趣的区域周围进行初始化，然后该轮廓慢慢收缩。snake=seg.active_contour(image_gray, points, alpha=0.06,beta=0.3) alpha和beta可以调整，alpha值越高，轮廓的收缩速度越快，beta越大收缩越慢。
  • 随机Walker分割：在该方法中，用户以交互方式标记少量的像素，这些像素称为标签。然后假设每个未标记的像素释放一个随机Walker，然后可以确定随机Walker从每个未标记像素开始到达一个预标记像素的概率。通过将每个像素分配给计算出来的概率值最大的标签，可以获得高质量的分割图像。随机Walker算法需要一个标签图像作为输入。image_segmented=seg.random_walker(image_gray, image_labels, beta=3000)
• 无监督分割算法：不需要先验知识，将图像自动细分到有意义的区域。用户仍然可以通过调整某些设置以获得想要的输出。
  • SLIC(简单线性迭代聚类)：使用了k-means算法，接收图像的所有像素值，并尝试将他们分离到给定数量的子区域中。image_slic=seg.slic(image, n_segments=200)，将图像的每个子图像或子区域像素设置为该区域像素的平均值color.label2rgb(image_slic, image,kind='avg)
  • Felzenszwalb算法：使用了最小生成树的聚类算法，不需设置图像将被分割成多少个集群，它将运算并生成尽可能多的适合它的集群。image_felzenszwalb=seg.felzenszwalb(image)，可以通过np.unique(image_felzenszwalb).size计算相互独立的区域数。使用区域像素平均值对子区域重新着色color.label2rgb(image_felzenszwalb, image, kind='avg')。

参考资料

计算机视觉之图像分割—水平集方法_ACWE2001
水平集—那些我膜拜过的牛人2
水平集算法原理介绍
Level set method：Explanation
水平集函数演化方程的推导细节
水平集算法总结
图像分割之（一）概述
图像分割之（五）活动轮廓模型之Snake模型简介
基于深度学习的图像分割总结
图像分割（一）——原理概念
图像分割技术介绍
单张图片的无监督语义分割，理解算法，并改良原始代码(从30秒改到5秒)
一文概述Python的scikit-image模块进行图像分割