优化算法（从梯度下降到Adam算法）

从梯度下降、动量法、AdaGrad、RMSProp、AdaDelta到Adam算法总结。
1.优化与深度学习
在一个深度学习问题中，我能通常会预先定义一个损失函数。有了损失函数以后，我们就可以使用优化算法试图将其最小化。在优化中，这样的损失函数通常被称作优化问题的目标函数（objective function）。一般来说，优化算法通常只考虑最小化目标函数。其实，任何最大化问题都可以很容易地转换为最小化问题，只需令目标函数的相反数作为新的目标函数即可。
由于优化算法的目标函数通常是一个基于训练数据集的损失函数，优化的目标在于降低训练误差。而深度学习的目标在于降低泛化误差。为了降低泛化误差，除了使用优化算法降低训练误差以外，还需要注意应对过拟合。
深度学习中绝大多数目标函数都复杂。因此，很多优化问题并不存在解析解，而需要使用基于数值方法的优化算法找到近似解，即数值解。为了求得最小化目标函数的数值解，我们将通过优化算法有限次迭代模型参数来尽可能降低损失函数的值。优化在深度学习中有很多的挑战，下面是其中两个比较重要的挑战：
（1）局部最小值
（2）鞍点
局部最小值：对于目标函数$f(x)$，如果$f(x)$在$x$上的值比在$x$邻近的其他点的值更小，那么$f(x)$可能是一个局部最小值(local minimum)。如果$f(x)$在$x$上的值是目标函数在整个定义域上的最小值，那么$f(x)$是全局最小值(global minimum)。

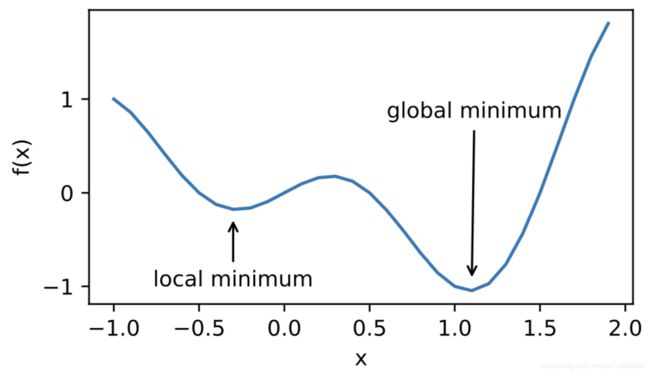
深度学习模型的目标函数可能有若干局部最优值。当一个优化问题的数值解在局部最优解附近时，由于目标函数有关解的梯度接近或变成零，最终迭代求得的数值解可能只能令目标函数局部最小化而非全局最小化。
鞍点：刚刚在局部最小值中提到，梯度接近或变成零可能是由于当前解在局部最优解附近造成的。事实上，另一种可能性是当前解在鞍点(saddle point)附近。

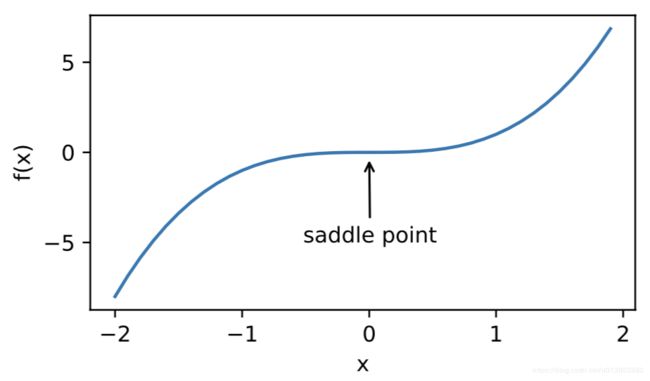
在深度学习中，虽然找到目标函数的全局最优解很难，但这并非必要。下面将介绍深度学习中常用的优化算法，它们在很多实际问题中都能够训练出十分有效的深度学习模型。

2.梯度下降和随机梯度下降

虽然梯度下降（gradient descent）在深度学习中很少被直接使用，但理解梯度的意义以及沿着梯度反方向更新自变量可能降低目标函数值的原因是学习后续优化算法的基础。

2.1 一维梯度下降

首先以简单的一维梯度下降为例，解释梯度下降算法可能降低目标函数的原因。假设连续可导的函数$f:\mathbb{R}\to \mathbb{R}$的输入和输出都是标量。给定绝对值足够小的数$ϵ$，根据泰勒展开公式，我们得到以下的近似：
$$f(x+ϵ)\approx f(x)+ϵf^{\prime }(x)$$

这里$f^{\prime }(x)$是函数$f$在$x$处的梯度。一维函数的梯度是一个标量，也称导数。
接下来，找到一个常数$\eta >0$使得$|\eta f^{\prime }(x)|$足够小，那么可以将$ϵ$替换为$-\eta f^{\prime }(x)$并得到：
$$f(x-\eta f^{\prime }(x))\approx f(x)-\eta f^{\prime }(x{)}^2$$

如果导数$f^{\prime }(x)\ne 0$，那么$\eta f^{\prime }(x{)}^2>0$，所以：
$$f(x-\eta f^{\prime }(x))\le f(x)$$

这意味着，如果通过
$$x\leftarrow \eta f^{\prime }(x)$$

来迭代$x$，函数$f(x)$的值可能会降低。因此在梯度下降中，我们先选取一个初始值$x$和常数$\eta >0$，然后不断通过上式来迭代$x$，直到达到停止条件，例如$f^{\prime }(x)$的值已足够小或迭代次数已达到某个值。
上述梯度下降算法中的正数$\eta$通常叫作学习率。这是一个超参数，需要人工设定，如果使用过小的学习率，会导致$x$更新缓慢从而需要更多的迭代才能得到较好的解。

2.2 多维梯度下降

下面考虑一种更广义的情况：目标函数的输入为向量，输出为标量。假设目标函数$f:{\mathbb{R}}^d\to \mathbb{R}$的输入是一个$d$维向量$\mathbf{x}=[x_1,x_2,...,x_d{]}^T$。目标函数$f(\mathbf{x})$有关$\mathbf{x}$的梯度是一个由$d$个偏导数组成的向量：
$${▽}_{x}f(\mathbf{x})={\left[\begin{array}{cccc}\frac{\partial f(\mathbf{x})}{\partial x_1},& \frac{\partial f(\mathbf{x})}{\partial x_2},& ...& ,\frac{\partial f(\mathbf{x})}{\partial x_d}\end{array}\right]}^T$$

为表示简洁，我们用$▽f(\mathbf{x})$代替$▽f_x(\mathbf{x})$。梯度中每个偏导数元素$\frac{\partial f(\mathbf{x})}{\partial x_i}$代表着$f$在$\mathbf{x}$有关输入$x_i$的变化率。为了测量$f$沿着单位向量$\mathbf{u}$(即∥u∥ = 1)方向上的变化率，在多元微积分中，我们定义$f$在$\mathbf{x}$上沿着$\mathbf{u}$方向的方向导数为：
$$D_{\mathbf{u}}f(\mathbf{x})=\underset{h\to 0}{\lim }\frac{f(\mathbf{x}+h\mathbf{u})-f(\mathbf{x})}{h}$$

根据导数性质，上面的方向导数可以改写为：
$$D_{\mathbf{u}}f(\mathbf{x})=▽f(\mathbf{x})\cdot \mathbf{u}$$

方向导数$D_{\mathbf{u}}f(\mathbf{x})$给出了$f$在$\mathbf{x}$上沿着所有可能方向的变化率。为了最小化$f$，我们希望找到$f$能被降低最快的方向。因此，我们可以通过单位向量$\mathbf{u}$来最小化方向导数$D_{\mathbf{u}}f(\mathbf{x})$。
由于$D_{\mathbf{u}}f(\mathbf{x})=||▽f(\mathbf{x})||\cdot ||\mathbf{u}||\cdot cos(\theta )=||▽f(\mathbf{x})||\cdot cos(\theta )$，其中$\theta$为梯度$▽f(\mathbf{x})$和单位向量$\mathbf{u}$之间的夹角，当$\theta =\pi$时，$cos(\theta )$取最小值-1。因此，当$\mathbf{u}$在梯度方向$▽f(\mathbf{x})$的相反方向时，方向导数$D_{\mathbf{u}}f(\mathbf{x})$被最小化。因此，我们可以通过梯度下降算法来不断降低目标函数$f$的值：
$$x\leftarrow x-\eta ▽f(\mathbf{x})$$

2.3 随机梯度下降

在机器学习或者深度学习里，目标函数通常是训练数据集中有关各个样本的损失函数的平均。设$f_i(\mathbf{x})$是有关索引为$i$的训练数据样本的损失函数，$n$是训练数据样本数，$\mathbf{x}$是模型的参数向量，那么目标函数定义为：
$$f(\mathbf{x})=\frac{1}{n}\sum _{i=1}^n{f}_i(\mathbf{x})$$

目标函数在$x$处的梯度计算为：
$$▽f(\mathbf{x})=\frac{1}{n}\sum _{i=1}^n▽f_i(\mathbf{x})$$

如果使用梯度下降，每次自变量迭代的计算开销为$O(n)$，它随着$n$线性增长。因此，当训练数据样本数很大时，梯度下降每次迭代的计算开销很高。
随机梯度下降(SGD)减少了每次迭代的计算开销。在随机梯度下降的每次迭代中，我们随机均匀采样一个样本索引$i\in 1,...,n$，并计算梯度$▽f_i(\mathbf{x})$来迭代$\mathbf{x}$:
$$\mathbf{x}\leftarrow \mathbf{x}-\eta ▽f_i(\mathbf{x})$$

可以看到每次迭代的计算开销从梯度下降的$O(n)$降到了常数$O(1)$。值得强调的是，随机梯度$▽f_i(\mathbf{x})$是对梯度 $▽f(\mathbf{x})$的无偏估计：
$$E_i▽f_i(\mathbf{x})=\frac{1}{n}\sum _{i=1}^n▽f_i(\mathbf{x})=▽f(\mathbf{x})$$

这意味着，平均来说，随机梯度是对梯度的一个良好的估计。

2.4 小批量随机梯度下降

在每一次迭代中，梯度下降使用整个训练数据集来计算梯度，因此它有时也被称为批量梯度下降算法（batch gradient descent）。而随机梯度下降在每次迭代中只随机采样一个样本来计算梯度。当然，我们还可以在每次迭代中随机均匀采样多个样本来组成一个小批量，然后使用整个小批量来计算梯度。这就是小批量随机梯度下降。
假设在时间步$t$，小批量随机梯度下降随机均匀采样一个由训练数据样本索引组成的小批量$B_t$。然后使用：
$${\mathbf{g}}_t\leftarrow ▽f_{B_t}({\mathbf{x}}_{t-1})=\frac{1}{|B|}\sum _{i\in B_t}▽f_i({\mathbf{x}}_{t-1})$$

然后给定学习率，小批量随机梯度下降对自变量的迭代如下：
$${\mathbf{x}}_t\leftarrow {\mathbf{x}}_{t-1}-{\eta }_t{g}_t$$

3.动量法

在梯度下降和随机梯度下降算法中我们提到，目标函数有关自变量的梯度代表了目标函数在自变量当前位置下降最快的方向。因此，梯度下降算法也叫作最陡下降。在每次迭代中，梯度下降根据自变量当前位置，沿着当前位置的梯度更新自变量。然而，如果自变量的迭代方向仅仅取决于自变量当前位置，这可能会带来一些问题。

3.1 梯度下降算法的问题

可以看到，同一位置上，目标函数在竖直方向(x2方向)比在水平方向上的斜率的绝对值更大。因此，给定学习率，梯度下降迭代自变量时会使得自变量在竖直方向上比在水平方向上移动幅度更大。那么，我们需要一个较小的学习率从而避免自变量在竖直方向上越过目标函数最优解。然而，这会造成自变量在水平方向上朝着最优解移动变慢。
但如果我们将学习率调的更大一点，此时自变量在竖直方向不断越过最优解并发散。

3.2 动量法

动量法的提出是为了解决梯度下降的上述问题。由于小批量随机梯度下降比梯度下降更为广义，后面都采用时间步·$t$的小批量随机梯度$g_t$
的定义。设时间步$t$的自变量为$x_t$，学习率为${\eta }_t$。在时间步0，动量法创建的速度变量$v_0$，并将其初始化为0.在时间步$t>0$，动量法对每次迭代的步骤做如下修改：
$$\begin{gathered} v_t\leftarrow \gamma v_{t-1}+{\eta }_t{g}_t \\ {x}_t\leftarrow x_{t-1}-v_t \end{gathered}$$
其中，动量超参数$0\le \gamma <1$。当$\gamma =0$的时候，动量法等价于小批量随机梯度下降算法。

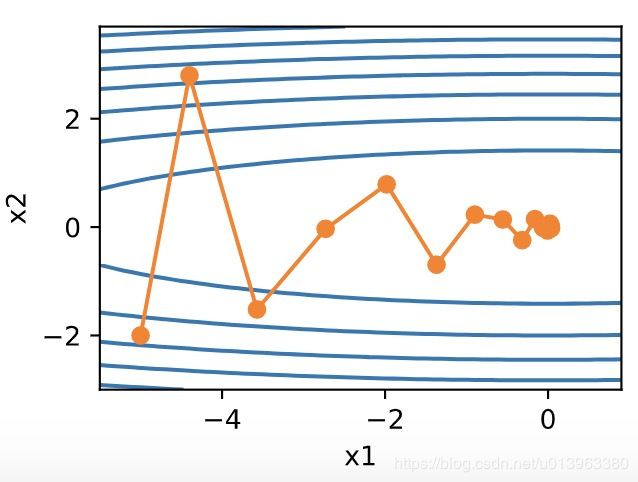
可以看到使用较小的学习率$\eta =0.4$和动量超参数$\gamma =0.5$。动量法在竖直方向上的移动更加平滑，且在水平方向上更快逼近最优解。
当使用较大的学习率$\eta =0.6$，此时自变量也不再发散。

指数加权移动平均理解动量法：由指数加权移动平均的形式可得，速度变量$v_t$实际上对序列{${\eta }_{t-i}{g}_{t-i}/(1-\gamma ):i=0,...,1/(1-\gamma )-1$}做了指数加权移动平均。换句话说，相比于小批量随机梯度下降算法，动量法在每个时间步的自变量更新量近似于将前者对应的最近$1/(1-\gamma )$个时间步的更新量做了指数加权移动平均后再除以$1-\gamma$。所以，在动量法中，自变量在各个方向上的移动幅度不仅取决于当前的梯度，还取决于过去的各个梯度在各个方向上是否一致。
小结：动量法使用了指数加权移动平均的思想。它将过去时间步的梯度做了加权平均，且权重按照时间步指数衰减。动量法使得相邻时间步的自变量更新在方向上更加一致。

4.AdaGrad算法

在之前介绍的优化算法中，目标函数自变量的每一个元素在相同时间步都使用同一个学习率$\eta$来自我迭代。
我们知道当$x_1$和$x_2$的梯度值由较大差异时，需要选择小的学习率使得自变量在梯度值较大的纬度上不发散。但这样会导致自变量在梯度值较小的纬度上迭代过慢。动量法依赖指数加权移动平均使得自变量的更新方向更加一致，从而降低散发的可能。
AdaGrad算法，它根据自变量在每个纬度的梯度值的大小来调整各个纬度上的学习率，从而避免统一的学习率难以适应所有纬度的问题[Adaptive subgradien methods for online learning and stochastic optimization]。

4.1 算法

AdaGrad算法会使用一个小批量随机梯度$g_t$按元素平方的累加变量$s_t$。在时间步0，AdaGrad算法将$s_0$中每个元素初始化为0.在时间步$t$，首先将小批量随机梯度$g_t$按照元素平方后累加到变量$s_t$：
$$s_t\leftarrow s_{t-1}+g_t\odot g_t$$
其中$\odot$是按元素相乘。接着，我们将目标函数自变量中每个元素的学习率通过按元素运算后重新调整一下：
$$x_t\leftarrow x_t-\frac{\eta }{\sqrt{s_t+ϵ}}\odot g_t$$
其中$\eta$是学习率，$ϵ$是为了维持数值稳定性而添加的常数，如$10^{-6}$。这里开方、除法和乘法的运算都是按照元素运算的。这些按元素运算使得目标函数自变量中每个元素都分别拥有自己的学习率。

4.2 特点

需要强调的是，小批量随机梯度按元素平方的累加变量$s_t$出现在学习率的分母项中。因此，如果目标函数有关自变量中某个元素的偏导数一直都很大，那么该元素的学习率将下降的越快；反之，如果目标函数有关自变量中某个元素的偏导数一直都较小，那么该元素的学习率将下降的较慢。然而，由于$s_t$一直在累加按元素平方的梯度，自变量中每个元素的学习率在迭代过程中一直再降低（或不变）。所以，当学习率在迭代早起降的较快且当前解依然不佳时，AdaGrad算法在迭代后期由于学习率过小，可能较难找到一个有用的解。
小结：AdaGrad算法在迭代过程中不断调整学习率，并让目标函数自变量中每个元素都分别拥有自己的学习率。使用AdaGrad算法时，自变量中每个元素的学习率在迭代过程中一直在降低（或不变）。

5.RMSProp算法

在AdaGrad算法中，因为调整学习率时分母上的变量$s_t$一直在累加按元素平方的小批量随机梯度，所以目标函数自变量每个元素的学习率在迭代过程中一直在降低（或不变）。
因此，当学习率在迭代早期降的较快且当前解依然不佳时，AdaGrad算法在迭代后期由于学习率过小，可能教难找到一个有用的解。为了解决这个问题，RMSProp算法对AdaGrad算法做了一点小小的修改。该算法源自Coursera上的一门课程，“机器学习的神经网络” [Divide the gradient by a running average of its recent magnitude]

动量法使用的是指数加权移动平均。不同于AdaGrad算法里状态变量$s_t$是截至时间步t所有小批量随机梯度$g_t$按元素平方和，RMSProp算法将这些梯度按元素平方做指数加权移动平均。具体来说，给定超参数$0\le \gamma <1$，RMSPro算法在时间步$t>0$计算
$$s_t\leftarrow \gamma s_t+(1-\gamma )g_t\odot g_t$$和AdaGrad算法一样，RMSProp算法将目标函数自变量中每个元素的学习率通过按元素运算重新调整，然后更新自变量$$x_t\leftarrow x_t-\frac{\eta }{\sqrt{s_t+ϵ}}\odot g_t$$
其中$\eta$是学习率，$ϵ$是为了维持数值稳定性而添加的常数，如$10^{-6}$。因为RMSProp算法的状态变量$s_t$是对平方项$g_t\odot g_t$的指数加权移动平均，所以可以看作是最近$1/(1-\gamma )$。如此一来，自变量每个元素的学习率在迭代过程中就不再一直降低（或不变）。

6.AdaDelta算法

除了RMSProp算法以外，另一个常用优化算法AdaDelta算法也针对AdaGrad算法在迭代后期可能较难找到有用解的问题做了改进[ADADELTA: an adaptive learning rate method.]。有意思的是，AdaDelta算法没有学习率这一超参数。
AdaDelta算法也像RMSProp算法一样，使用了小批量随机梯度$g_t$按元素平方的指数加权移动平均变量$s_t$。在时间步0，它的所有元素被初始化为0。给定超参数$0\le \rho <1$ （对应RMSProp算法中的$\gamma$），在时间步$t>0$，同RMSProp算法一样计算
$$s_t\leftarrow \rho s_{t-1}+(1-\rho )g_t\odot g_t$$
与RMSProp算法不同的是，AdaDelta算法还维护一个额外的状态变量$\Delta x_t$，其元素同样在时间步0时被初始化为0。我们使用$\Delta x_{t-1}$来计算自变量的变化量：
$$g_t^{{}^{\prime }}\leftarrow \sqrt{\frac{\Delta x_t+ϵ}{s_t+ϵ}}\odot g_t$$
其中$ϵ$是为了维持数值稳定性而添加的常数，如$10^{-5}$。接着更新自变量：
$$x_t\leftarrow x_{t-1}-g_t^{{}^{\prime }}$$
最后，我们使用$\Delta x_t$来记录自变量变化量$g_t^{{}^{\prime }}$按元素平方的指数加权移动平均：
$$\Delta x_t\leftarrow \rho \Delta x_{t-1}+(1-\rho )g_t^{{}^{\prime }}\odot g_t^{{}^{\prime }}$$
可以看到，如不考虑$ϵ$的影响，AdaDelta算法跟RMSProp算法的不同之处在于使用$\sqrt{\Delta x_{t-1}}$来替换超参数$\eta$。

7.Adam算法

Adam算法在RMSProp算法基础上对小批量随机梯度也做了指数加权移动平均[Adam: A method for stochastic optimization]
Adam算法使用了动量变量$v_t$和RMSProp算法中小批量随机梯度按元素平方的指数加权移动平均变量$s_t$，并在时间步0将它们中每个元素初始化为0。给定超参数$0\le {\beta }_1<1$（算法作者建议设置为0.9），时间步$t$的动量变量$v_t$即小批量随机梯度$g_t$的指数加权移动平均：
$$v_t\leftarrow {\beta }_1{v}_{t-1}+(1-{\beta }_1)g_t$$

和RMSProp算法中一样，给定超参数$0\le {\beta }_2<1$（算法作者建议设置为0.999），将小批量随机梯度按元素平方后的项$g_t\odot g_t$做指数加权平均得到$s_t$：
$$s_t\leftarrow {\beta }_2{s}_{t-1}+(1-{\beta }_2)g_t\odot g_t$$

由于我们将$v_0$和$s_0$中的元素都初始化为0，在时间步$t$我们得到$v_t=(1-{\beta }_1){\sum }_{i=1}^t{\beta }_1^{t-i}{g}_i$。将过去各时间步小批量随机梯度的权值相加，得到$(1-{\beta }_1){\sum }_{i=1}^t{\beta }_1^{t-i}=1-{\beta }_1^t$。需要注意的是，当$t$较小时，过去各时间步小批量随机梯度权值之和会较小。例如，当${\beta }_1=0.9$时，$v_1=0.1g_1$。为了消除这样的影响，对于任意时间步$t$，我们可以将$v_t$再除以$1-{\beta }_1^t$，从而使过去各时间步小批量随机梯度权值之和为1。这也叫作偏差修正。在Adam算法中，我们对变量$v_t$和$s_t$均作偏差修正：
$${\hat{v}}_t\leftarrow \frac{v_t}{1-{\beta }_1^t}$$ $${\hat{s}}_t\leftarrow \frac{s_t}{1-{\beta }_2^t}$$

接下来，Adam算法使用以上偏差修正后的变量${\hat{v}}_t$和${\hat{s}}_t$，将模型参数中每个元素的学习率通过按元素运算重新调整：
$$g_t^{{}^{\prime }}\leftarrow \frac{\eta {\hat{v}}_t}{\sqrt{{\hat{s}}_t}+ϵ}$$其中$\eta$使学习率，$ϵ$使为了维持数值稳定而添加的常数，如$10^{-8}$。和AdaGrad算法、RMSProp算法以及AdaDelta算法一样，目标函数自变量中每个元素都分别拥有自己的学习率。最后使用$g_t^{{}^{\prime }}$迭代自变量：
$$x_t\leftarrow x_{t-1}-g_t^{{}^{\prime }}$$

---

【参考文献】：
【1】全文参考动手学习DP