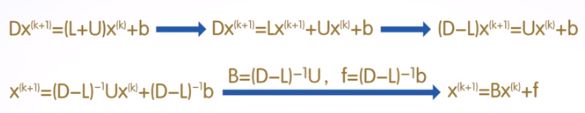Matlab数值微积分与方程求解

课程参考：https://www.icourse163.org/learn/CSU-1002475002?tid=1206743216#/learn/content?type=detail&id=1211570840&cid=1214317955

一、数值微分与数值积分

数值微积分不同于高等数学中的微积分，高等数学是对函数采用解析方法求解，数值微积分适合求解没有或很难求出微分或积分表达式的问题的计算。

1.1 数值微分

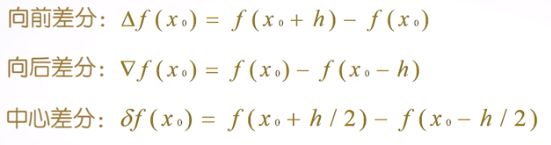
当h非常小时，得到：

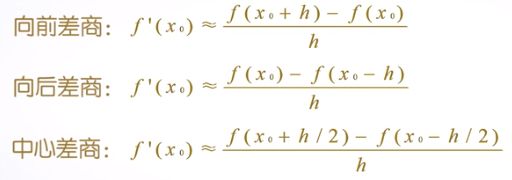
函数f(x)在$x_0$点的微分，接近于函数在该点的差分，而f(x)在$x_0$的导数，接近于函数在该点的差商。

%% 6.1 数值微分与数值积分
%例1  设f(x)=sinx，在[0，2π]范围内随机采样，计算f'(x)的近似值，并与理论值f'(x)=cosx 进行比较。
x=[0,sort(2*pi*rand(1,5000)),2*pi];
y=sin(x);
f1=diff(y)./diff(x);
f2=cos(x(1:end-1));
plot(x(1:end-1),f1,x(1:end-1),f2);
d=norm(f1-f2)  %范数

1.2 数值积分

当被积函数的原函数无法用初等函数表示时，或被积函数是用表格形式给出的，这时就需要用数值解法来求定积分的近似值，求定积分的数值方法多种多样，如梯形法、辛普森法、高斯求积公式等。

在每一个小的区间上，定积分的值可以近似求得，从而避免了牛顿莱布尼兹公式需要寻求原函数的困难。

quad函数

quadl函数

%例2  分别用quad函数和quadl函数求定积分的近似值，并在相同的积分精度下，比较被积函数的调用次数。
format long
f=@(x) 4./(1+x.^2);
[I,n]=quad(f,0,1,1e-8)
 
[I,n]=quadl(f,0,1,1e-8)
 
(atan(1)-atan(0))*4
 
format short

integral函数

%例3 求定积分。 
%被积函数文件fe.m：
function f=fe(x)
f=1./(x.*sqrt(1-log(x).^2));

I=integral(@fe,1,exp(1))

quadgk函数

求振荡函数的定积分

%例4  求定积分。
%被积函数文件fsx.m：
function f=fsx(x)
f=sin(1./x)./x.^2;

I=quadgk(@fsx,2/pi,+Inf)

**当函数关系表达式不知道，只有实验测定的一组样本点和样本值，这样就无法使用quad等函数来计算定积分。**针对这种情况，有以下方法进行求解：

trapz函数

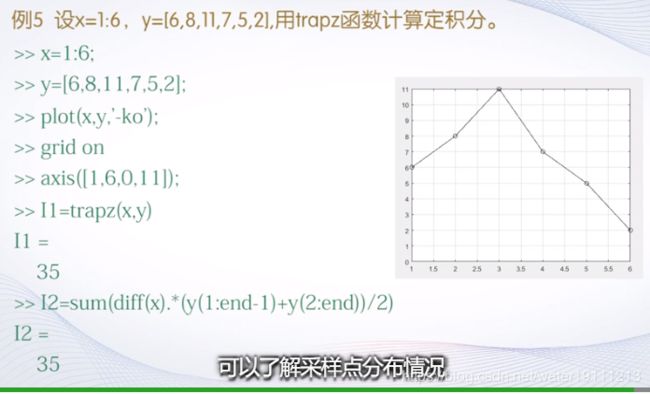
%例5  设x=1:6，y=[6,8,11,7,5,2],用trapz函数计算定积分。
x=1:6;
y=[6,8,11,7,5,2];
plot(x,y,'-ko');
grid on
axis([1,6,0,11]);
I1=trapz(x,y)

I2=sum(diff(x).*(y(1:end-1)+y(2:end))/2)   %梯形面积公式

多重定积分的数值求解

% 例6  分别求二重积分和三重积分。 
f1=@(x,y) exp(-x.^2/2).*sin(x.^2+y);
I1=quad2d(f1,-2,2,-1,1)

f2=@(x,y,z) 4*x.*z.*exp(-z.*z.*y-x.*x);
I2=integral3(f2,0,pi,0,pi,0,1)

二、线性方程组求解

2.1 直接法

就是在不考虑舍入误差的情况下，通过有限步的矩阵初等运算，来求得方程组精确解的方法。

2.1.1 高斯（Gauss）消去法

2.1.2 列主元消去法

是目前计算机上求解线性方程组的标准算法，其特点就是通过消元，将一般线性方程组的求解问题转化为三角方程组的求解问题。

A=[2,1,-5,1;1,-5,0,7;0,2,1,-1;1,6,-1,-4];
b=[13,-9,6,0]';  %b是列向量
x=A\b

可以用矩阵求逆函数来求解线性方程组，即x等于A的逆矩阵乘以b,但在实际计算中，不建议使用求逆矩阵的方法，因为求逆方法需要更多的计算量，它先求逆矩阵，在求矩阵乘法，而左除运算就只有一次除法，况且，求逆算法给出的可能还是一个不精确的答案。

2.1.3 矩阵的三角分解法

矩阵分解是设计算法的重要技巧，是指将一个给定的矩阵分解成若干个特殊类型矩阵的乘积，从而将一个一般的矩阵计算问题，转化为几个易求的特殊矩阵的计算问题。这种方法的优点是运算速度快，可以节省存储空间。

LU分解

将一个n阶矩阵表示为一个下三角矩阵和一个上三角矩阵的乘积，线性代数中已证明，只要方阵是非奇异的，LU分解总是可以进行的。

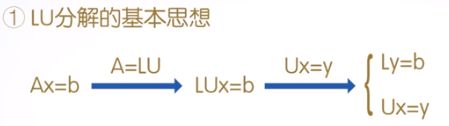
对于三角矩阵很容易求解，可以先求解向量y使Ly等于b，再求解Ux等于y

使用第一种方式，矩阵L往往不是下三角阵，但可以通过行交换，成为一个下三角阵。

%例2  用LU分解求解例1中的线性方程组。
A=[2,1,-5,1;1,-5,0,7;0,2,1,-1;1,6,-1,-4];
b=[13,-9,6,0]';
[L,U]=lu(A);
x=U\(L\b)
%第二种格式
[L,U,P] = lu(A);
x = U\(L\P*b)

QR分解

Cholesky分解(乔累斯分解)

2.2 迭代法

就是先给定一个解的初始值，然后按照一定的迭代算法进行逐步逼近，求出更精确的近似解的方法。
不断用变量的原值推出它的新值的过程，是用计算机解决问题的一种基本方法。

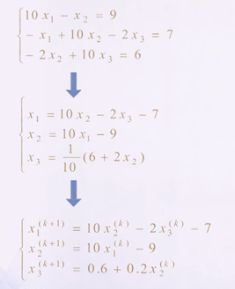
2.2.1 雅克比（Jacobi）迭代法

对于线性方程组Ax=b，如果A为非奇异方阵且主对角线元素不等于0，则可将A分解为D-L-U，其中D为对角阵，其元素为A的对角元素，L与U为A的下三角阵取反和上三角阵取反。

%雅可比迭代法的函数文件jacobi.m：
function [y,n]=jacobi(A,b,x0,ep)
D=diag(diag(A));
L=-tril(A,-1);
U=-triu(A,1);
B=D\(L+U);
f=D\b;
y=B*x0+f;
n=1;
while norm(y-x0)>=ep
    x0=y;
    y=B*x0+f;
    n=n+1;
end

2.2.2 高斯-赛德尔（Gauss-Serdel）迭代法

用新分量代替旧分量，精度会高一些。

%Gauss-Serdel迭代法的函数文件gauseidel.m：
function [y,n]=gauseidel(A,b,x0,ep)
D=diag(diag(A));
L=-tril(A,-1); 
U=-triu(A,1);
B=(D-L)\U;
f=(D-L)\b;
y=B*x0+f;
n=1;
while norm(y-x0)>=ep
    x0=y;
    y=B*x0+f;
    n=n+1;
end

%例3  分别用雅可比迭代法和高斯-赛德尔迭代法求解线性方程组。设迭代初值为0，迭代精度为10^(-6)。
A=[4,-2,-1;-2,4,3;-1,-3,3];
b=[1,5,0]';
[x,n]=jacobi(A,b,[0,0,0]',1.0e-6)

[x,n]=gauseidel(A,b,[0,0,0]',1.0e-6)

%例4  分别用雅可比迭代法和高斯-赛德尔迭代法求解下列线性方程组，看是否收敛。
A=[1,2,-2;1,1,1;2,2,1];
b=[9;7;6];
[x,n]=jacobi(A,b,[0;0;0],1.0e-6)

[x,n]=gauseidel(A,b,[0;0;0],1.0e-6)

三、线性方程组应用举例

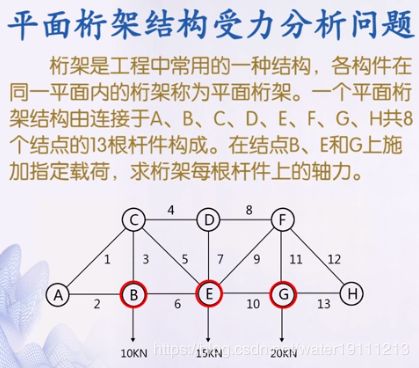
3.1 平面桁架结构受力分析

%1．平面桁架结构受力分析问题
alpha=sqrt(2)/2;
A=[0,1,0,0,0,-1,0,0,0,0,0,0,0;
   0,0,1,0,0,0,0,0,0,0,0,0,0;
   alpha,0,0,-1,-alpha,0,0,0,0,0,0,0,0;
   alpha,0,1,0,alpha,0,0,0,0,0,0,0,0;
   0,0,0,1,0,0,0,-1,0,0,0,0,0;
   0,0,0,0,0,0,1,0,0,0,0,0,0;
   0,0,0,0,alpha,1,0,0,-alpha,-1,0,0,0;
   0,0,0,0,alpha,0,1,0,alpha,0,0,0,0;
   0,0,0,0,0,0,0,0,0,1,0,0,-1;
   0,0,0,0,0,0,0,0,0,0,1,0,0;
   0,0,0,0,0,0,0,1,alpha,0,0,-alpha,0;
   0,0,0,0,0,0,0,0,alpha,0,1,alpha,0;
   0,0,0,0,0,0,0,0,0,0,0,alpha,1];
b=[0;10;0;0;0;0;0;15;0;20;0;0;0];
f=A\b;
disp(f')

正数表示拉力，负数表示压力

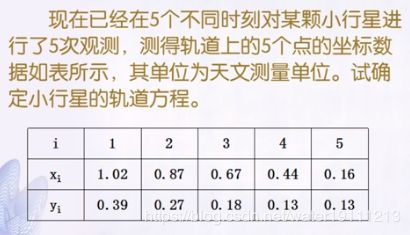
3.2 小行星运动轨道计算

%2．小行星运行轨道计算问题
xi=[1.02,0.87,0.67,0.44,0.16];
yi=[0.39,0.27,0.18,0.13,0.13];
A=zeros(length(xi));
for i=1:length(xi)
    A(i,:)=[xi(i)*xi(i),2*xi(i)*yi(i),yi(i)*yi(i),2*xi(i),2*yi(i)];
end
b=-ones(length(xi),1);
ai=A\b

%或者：
xi=[1.02,0.87,0.67,0.44,0.16]';
yi=[0.39,0.27,0.18,0.13,0.13]';
A=[xi.*xi,2*xi.*yi,yi.*yi,2*xi,2*yi];
b=-ones(length(xi),1);
ai=A\b

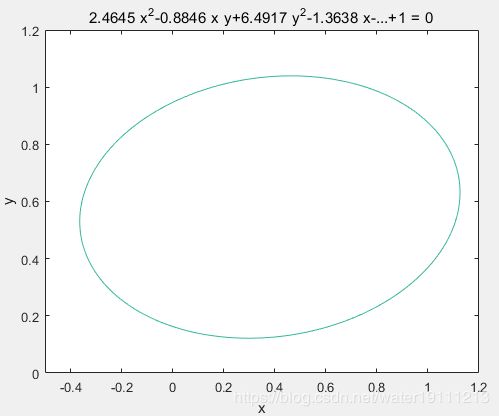
f=@(x,y) 2.4645*x.^2-0.8846*x.*y+6.4917*y.^2-1.3638*x-7.2016*y+1;
h=ezplot(f,[-0.5,1.2,0,1.2]);

四、非线性方程求解与函数极值计算

4.1 非线性方程求解

4.1.1 fzero函数

$x_0$是初始值

%例1  求f(x)=0在x0=-5和x0=1作为迭代初值时的根。
f=@(x) x-1./x+5;
x1=fzero(f,-5)
 
x2=fzero(f,1)
 
x3=fzero(f,0.1) 

求得：

x1 =-5.1926
x2 =0.1926
x3 =3.7372e-16

显然，x3不是方程的根，所以在使用fzero函数时，初值的选取非常关键。
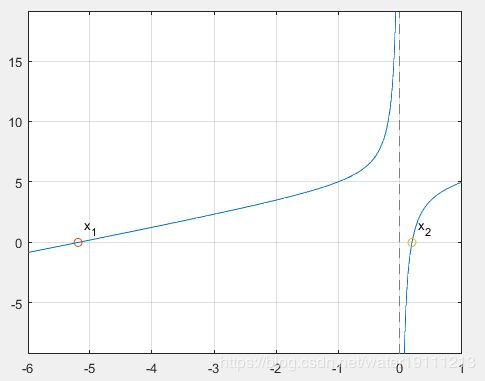
作出曲线图，观察根的分布位置：

figure,
fplot(@(x) x-1./x+5,[-6,1])
hold on
scatter (x1,0)
scatter(x2,0)
text(x1+0.1,1.25,'x_1')
text(x2+0.1,1.25,'x_2')
grid on

我们也可以使用fsolve来求方程的根：

4.1.2 fsolve函数

f=@(x) x-1./x+5;
x1=fsolve(f,-5,optimset('Display','off'))
 
x2=fsolve(f,1,optimset('Display','off'))
 
x3=fsolve(f,0.1,optimset('Display','off'))

求得：

x1 =-5.1926
x2 =0.1926
x3 =0.1926

可以看出：fsolve相较与fzero函数，功能更强，可以求解非线性方程组。

%例2  求下列方程组在（1，1，1）附近的解并对结果进行验证。
f=@(x) [sin(x(1))+x(2)+x(3)^2*exp(x(1)),x(1)+x(2)+x(3),x(1)*x(2)*x(3)];    %定义一个匿名函数，建立方程左边的方程组
f([1,1,1])   %匿名函数调用方法
 
x=fsolve(f,[1,1,1],optimset('Display','off'))  %在给定初值下调用fsolve函数，求方程的根
 
f(x)   %检验结果是否正确

4.2 函数极值的计算

4.2.1 无约束最优化问题

[xmin,fmin] = fminbnd(filename,x1,x2,option)

求一元函数在$x_1$到$x_2$开区间中的极小值点xmin和最小值fmin。

[xmin,fmin] = fminsearch(filename,x0,option)

基于单纯行算法，求多元函数的极小值点xmin和最小值fmin。

[xmin,fmin] = fminnunc(filename,x0,option)

基于拟牛顿法求多元函数的极小值点xmin和最小值fmin。

%例3  求函数f(x)在区间(-10，-1)和(1，10)上的最小值点。
f=@(x) x-1./x+5;
[xmin,fmin]=fminbnd(f,-10,-1)
[xmin,fmin]=fminbnd(f,1,10)

结果：

xmin =-9.9999
fmin =-4.8999

xmin =1.0001
fmin =5.0001

4.2.2 有约束最优化问题

fmincon函数

[xmin,fmin] = fmincon(filename,x0, A,b,Aeq,beq,Lbnd,Ubnd,NonF,option)

%例4  求解有约束最优化问题。
f=@(x) 0.4*x(2)+x(1)^2+x(2)^2-x(1)*x(2)+1/30*x(1)^3;
x0=[0.5;0.5];
A=[-1,-0.5;-0.5,-1]; %定义线性不等式约束
b=[-0.4;-0.5];    %定义线性不等式约束
lb=[0;0];   %解的下界，其余约束均为空
option=optimset('Display','off');  %定义优化器
[xmin,fmin]=fmincon(f,x0,A,b,[],[],lb,[],[],option) %调用fmincon函数

结果如下：

xmin =
    0.3396
    0.3302
fmin =
    0.2456    

4.3 最小值问题应用实例

%例5  要使每周送货车的里程最小，仓库应建在xy平面的什么位置？
a=[10,30,16.667,0.555,22.2221];
b=[10,50,29,29.888,49.988];
c=[10,18,20,14,25];
f=@(x) sum(c.*sqrt((x(1)-a).^2+(x(2)-b).^2));
[xmin,fmin]=fminsearch(f,[15,30])

结果显示：

xmin =
   19.8143   41.1247
fmin =
   1.3618e+03

这样问题变为一个有约束最优化问题。
即在原来函数的求解中，加入非线性约束条件，我们可以建一个函数。

function [c,h]=funny(x)
c=[];
h=x(2)-x(1)^2;

应用例5的命令：

a=[10,30,16.667,0.555,22.2221];
b=[10,50,29,29.888,49.988];
c=[10,18,20,14,25];
f=@(x) sum(c.*sqrt((x(1)-a).^2+(x(2)-b).^2));
[xmin,fmin]=fmincon(f,[15,30],[],[],[],[],[],[],'funny')

结果显示：

xmin =
    5.9363   35.2402
fmin =
   1.6676e+03    

五、常微分方程数值求解

5.1 一般概念

单步法和多步法

5.2 求解函数

Option常用属性包括：相对误差值（默认值10e-3次方），绝对误差值（默认值是10e-6次方）

例如：ode23采用2阶龙格库塔算法，用3阶公式做误差估计来调节步长，具有低等精度。
ode45 采用4阶龙格库塔算法，用5阶公式做误差估计来调节步长，具有中等精度。
ode23s中的s代表“stiff”，表示函数适用于刚性方程

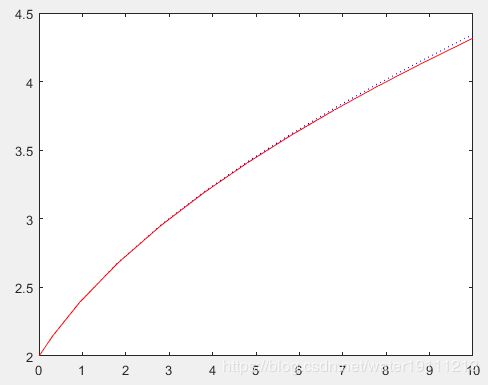
% 例1  求解微分方程初值问题，并与精确解进行比较。 
f=@(t,y) (y^2-t-2)/4/(t+1);
[t,y]=ode23(f,[0,10],2);   %求数值解
y1=sqrt(t+1)+1;     %精确解
plot(t,y,'b:',t,y1,'r');  %比较

结果：

% 例2  已知一个二阶线性系统的微分方程，取a=2，绘制系统的时间响应曲线和相平面图。
f=@(t,x) [-2,0;0,1]*[x(2);x(1)];  %定义函数
[t,x]=ode45(f,[0,20],[1,0]);     %求微分方程的解
subplot(2,2,1);plot(t,x(:,2));
subplot(2,2,2);plot(x(:,2),x(:,1));

5.3 刚性问题

对于刚性问题，数值解必须取很小步长才能获得满意的结果，导致计算量会大大增加。因此，解决刚性问题需要有专门方法，非刚性算法可以求解刚性问题，只是需要很长的计算时间。

先用ode45函数求解：

% 例3  假如点燃一个火柴，已知火焰球简化模型，分析λ的大小对方程求解过程的影响。
lamda=0.01;
f=@(t,y) y^2-y^3;
tic;[t,y]=ode45(f,[0,2/lamda],lamda);toc  %tic函数记录当前时间，toc函数记录语句完成时间
disp(['ode45计算的点数'  num2str(length(t))]);

结果显示：

时间已过 0.034623 秒。
ode45计算的点数157

表明：这时常微分方程不算很刚性。
接下来改变lamda的步长

lamda=1e-5;
f=@(t,y) y^2-y^3;
tic;[t,y]=ode45(f,[0,2/lamda],lamda);toc
disp(['ode45计算的点数' num2str(length(t))]);

结果显示：

时间已过 2.262576 秒。
ode45计算的点数120565

表明：这时常微分方程表现为刚性。
对于刚性问题，我们需要改变算法，用带“s”的函数求解，求解时间与求解点数明显减少：

lamda=1e-5;
f=@(t,y) y^2-y^3;
tic;[t,y]=ode15s(f,[0,2/lamda],lamda);toc
disp(['ode15s计算的点数' num2str(length(t))]);

时间已过 0.198160 秒。
ode15s计算的点数98

六、常微分方程应用举例

若lamda等于0，两个种群就不发生相互作用，兔子生存状态最好，而狐狸因饥饿而死亡；若lamda大于0，狐狸捕捉兔子，导致兔子数量减少，而狐狸数量增加，该非线性系统的解，无法用其他已知函数来表达，而必须数值求解。事实表明：该系统解，具有周期性，其周期性取决于初始条件。

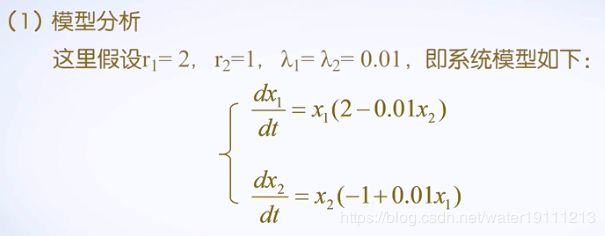
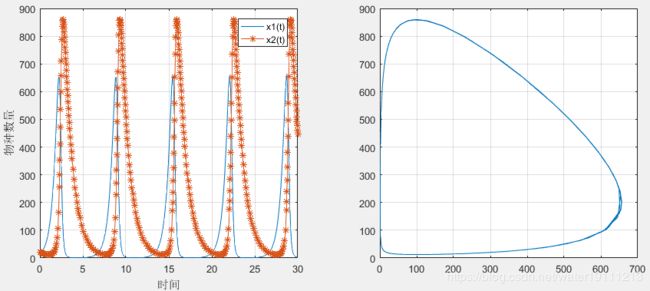
% 第①问：
rabbitFox=@(t,x) [x(1)*(2-0.01*x(2));x(2)*(-1+0.01*x(1))];
[t,x]=ode45(rabbitFox,[0,30],[300,150])
subplot(1,2,1);plot(t,x(:,1),'-',t,x(:,2),'-*');
legend('x1(t)','x2(t)');
xlabel('时间');ylabel('物种数量');
grid on
subplot(1,2,2);plot(x(:,1),x(:,2))
grid on

% 第2问
rabbitFox=@(t,x) [x(1)*(2-0.01*x(2));x(2)*(-1+0.01*x(1))];
[t,x]=ode45(rabbitFox,[0,30],[15,22])
subplot(1,2,1);plot(t,x(:,1),'-',t,x(:,2),'-*');
legend('x1(t)','x2(t)');
xlabel('时间');ylabel('物种数量');
grid on
subplot(1,2,2);plot(x(:,1),x(:,2))
grid on

可以看出：周期tp接近于6.62

% 第3问
rabbitFox=@(t,x) [x(1)*(2-0.01*x(2));x(2)*(-1+0.01*x(1))];
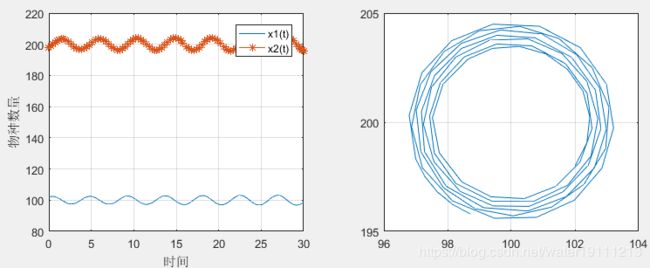
[t,x]=ode45(rabbitFox,[0,30],[102,198])
subplot(1,2,1);plot(t,x(:,1),'-',t,x(:,2),'-*');
legend('x1(t)','x2(t)');
xlabel('时间');ylabel('物种数量');
grid on
subplot(1,2,2);plot(x(:,1),x(:,2))
grid on

周期tp大致接近于4.92

% 第④问：
% 取λ=0.01， 所以稳定平衡点（1/λ，2/λ）即是（100，200），以此点作为初值时，画出其图像。
rabbitFox=@(t,x) [x(1)*(2-0.01*x(2));...
                  x(2)*(-1+0.01*x(1))];
[t,x]=ode45(rabbitFox,[0,30],[100,200]);
plot(t,x(:,1),'-o',t,x(:,2),'-*');
legend('x1(t)-兔子','x2(t)-狐狸');
xlabel('时间');
ylabel('物种数量');

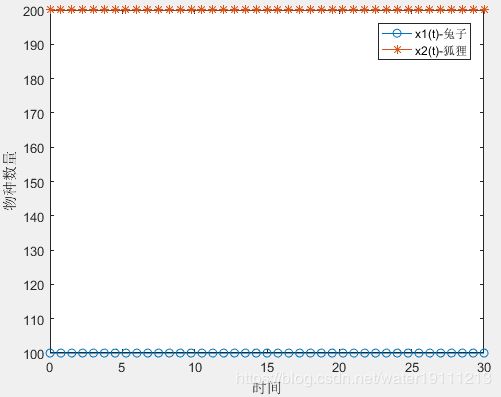
可以发现：当兔子和狐狸的初始值分别取100和200时，兔子和狐狸的数量不随时间发生变化。

对原方程进行修改，可以防止兔子数量无限制的增长。

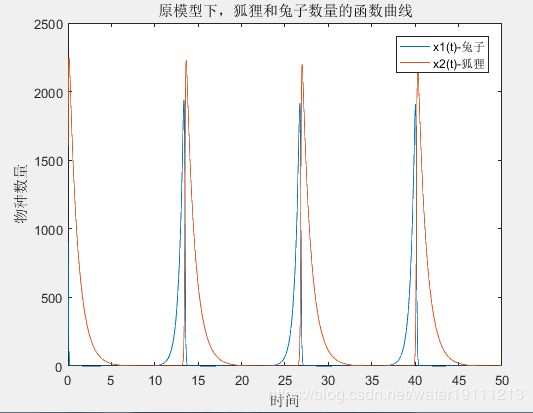
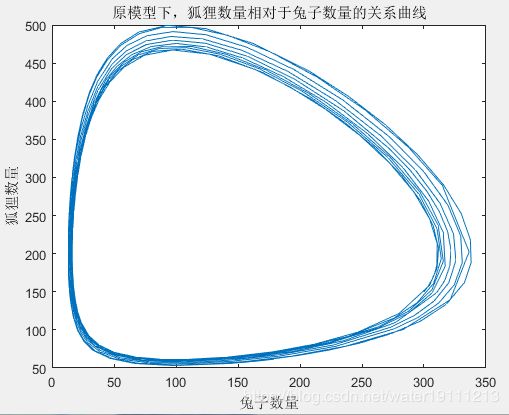
% 第①问：在原模型下，绘制狐狸和兔子数量的时间函数曲线。
rabbitFox=@(t,x) [x(1)*(2-0.01*x(2));...
                  x(2)*(-1+0.01*x(1))];
[t,x]=ode45(rabbitFox,[0,50],[900,1600]);
plot(t,x(:,1),t,x(:,2));
legend('x1(t)-兔子','x2(t)-狐狸');
xlabel('时间');
ylabel('物种数量');
title('原模型下，狐狸和兔子数量的函数曲线');

% 第②问：在改进模型下，狐狸和兔子数量的时间函数曲线。
rabbitFox=@(t,x) [2*x(1)*(1-x(1)/400-0.005*x(2));...
                 x(2)*(-1+0.01*x(1))];
[t,x]=ode45(rabbitFox,[0,50],[300,150]);
plot(t,x(:,1),t,x(:,2));
legend('x1(t)-兔子','x2(t)-狐狸');
xlabel('时间');
ylabel('物种数量');
title('改进模型下，狐狸和兔子数量的函数曲线');