【微型计算机原理与接口技术】计算机中的信息表示
计算机中的信息表示
- 计算机中的数制
- 常用计数值
- 数值转换
- 2、8、16进制数 ——> 10进制数
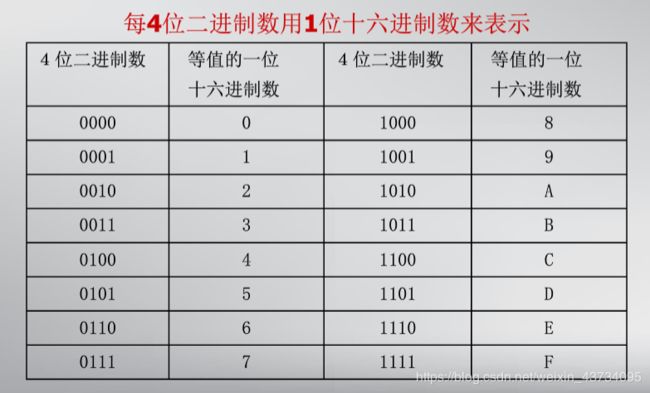
- 2进制数 ——> 16进制数
- 16进制数 ——> 2进制数
- 10进制数 ——> 2进制数
- 10进制整数 ——> 2进制数
- 10进制纯小数 ——> 2进制数
- 10进制带小数 ——> 2进制数
- 计算机中的数据编码
- 字符的编码——ASCII码
- 10进制数的2进制编码 —— BCD码
- 有符号数的编码（码制）—— 原反补码
- 原码
- 反码
- 补码
- 无符号数
- 小结
- 整数补码运算
- “模”的概念
- 整数补码的运算
- 求补运算
- 整数补码的加减运算
- 进位和溢出
- 计算机怎样表示进位和溢出？
- 程序员如何判断溢出？
计算机中的数制
常用计数值
- 十进制数： 0~9，基数为10，编程时使用（D）
- 二进制数： 计算机内部信息存储、运算和输入/输出都是二进制数（B）
- 十六进制数： 为了书写阅读方便，常常采用十六进制数（H）来表示二进制数。
人们最常用的是十进制，但在计算机中为了物理实现的方便，采用的是二进制。
十六进制与二进制的关系：
数值转换
2、8、16进制数 ——> 10进制数
算法：每位的代码和该位的权值相乘，再求累加和。
2进制数 ——> 16进制数
算法：四位2进制数为一组，每组用等值的16进制代换。
16进制数 ——> 2进制数
算法：一位16进制数用等值的四位2进制数代换。
10进制数 ——> 2进制数
10进制整数 ——> 2进制数
算法：除2取余，直到商为零为止，得到的余数倒排。
10进制纯小数 ——> 2进制数
算法：小数部分乘2取整，直到乘积的小数部分为0时止，整数部分顺排。
10进制带小数 ——> 2进制数
算法：整数、纯小数分别计算，再合并。
计算机中的数据编码
字符的编码——ASCII码
计算机中常用的输入 / 输出设备（键盘、显示器、打印机）处理的数都是字符。
例如：英文的大小写字母（A-Z，a-z），数字符号（0-9）以及其他常用符号（%、+ 等）。
采用美国标准信息交换码（ASCII）对字符进行编码。
采用七位二进制编码来表示一个字符。该编码方案中共有128个字符。（27=128）
查询某个字符时，高位在前，低位在后，例如：
键盘输入“1”，实际写入键盘存储区的是 31H，即 00110001B。
键盘输入“A”，实际写入键盘存储区的是 41H，即 01000001B。
想要显示“0”，应把 30H 即 00110000B —> 显示存储区。
想要显示“F”，应把 46H 即 01000110B —> 显示存储区。
程序设计的需要，要求牢记以下相关字符的 ASCII 码：
- 0 ~ 9 的 ASCII 码为：30H ~ 39H
- A ~ F 的 ASCII 码为：41H ~ 46H
- 回车符的 ASCII 码为：0DH
- 换行符的 ASCII 码为：0AH
10进制数的2进制编码 —— BCD码
- 采用2进制数对每一位10进制数进行编码所得到的数叫做BCD码。
- BCD码有多种形式，最常用的是8421BCD码，它是四位2进制数对一个10进制数进行编码，这四位2进制码的值就是被编码的一位10进制数的值。
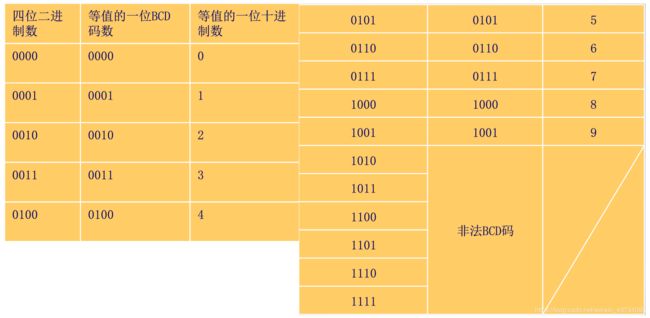
BCD码在计算机中的存储分为紧凑型和非紧凑型两种：
有符号数的编码（码制）—— 原反补码
在计算机中如何表示正负？
计算机只能识别0和1组成的数或代码，所以有符号数的符号也只能用0和1来表示；
即符号数值化，并作为数的一部分参与运算。
真值和机器数的概念：
- 真值：一个数的数值，用 “+” 表示正数，用 “-” 表示负数。
- 字长：是计算机在同一时间内处理二进制数的位数。是CPU的一个主要技术指标。
对有符号数来讲，是包括符号位在内的一个二进制有符号数占有的位数。
由于机器数的数值部分的表示方法不同，有符号数可有三种表示方法（即机器数有三种形式），分别叫做：原码、反码、补码。
数X的原码记作 [X]原 ，反码记作 [X]反 ，补码记作 [X]补
原码
最高位为符号位（0+，1-），数值位部分就是该数的绝对值。
反码
把最高位规定为符号位，数值部分对正数是其绝对值；
对于负数则是其绝对值按位取反（即1变0，0变1）。
补码
正数的原码，反码，补码相同。
负数的数值位部分为其绝对值按位取反后末位加1所得。
无符号数
某些处理的数据都是正数，最小数为0。可取消符号位，机器数的最高位是数值位。
机器数的物理意义是由程序员定的。
例如，机器数10000101对应的真值是几？
小结
①机器数比真值数多一个符号位。
②正数的原、反、补码与真值数相同。
③负数原码的数值部分与真值相同；
负数反码的数值部分为真值数按位取反；
负数补码的数值部分为真值数按位取反末位加1。
④没有负零的补码，或者说负零的补码与正零的补码相同，都是 00000000。
⑤由于补码表示的机器数更适合运算，为此，计算机系统中负数一律用补码表示。
⑥机器数的数值范围（设机器数字长=n位，用来表示整数）
整数补码运算
“模”的概念
一个计量器的最大容量称为该计量器的“模”；
四位计数器能存 0000 ~ 1111 共 16 个数，模 = 24
八位计数器能存 0000,0000 ~ 1111,1111 共 256 个数，模 = 28
十六位计数器能存 0000,0000,0000,0000 ~ 1111,1111,1111,1111 共 65536 个数，模 = 216
整数补码的运算
求补运算
设一个数的真值数值部分用X来表示，按照补码的编码规则，可以计算得到：[+X]补
对 [+X]补 按位取反末位+1，就得到 [-X]补
整数补码的加减运算
- [ x + y ]补 = [ x ]补 + [y]补
- [ x - y ]补 = [ x ]补 - [y]补
条件：
- 符号位参与运算
- 以 2n为模（n为字长）
- 当真值满足下列条件时，结果是正确的，否则结果错误
-2n-1 <= x, y, x+y, x-y < +2n-1
看一道例题，结果是正确的。
再看一道结果错误的例题。
由此可见，定字长的机器，表示的数值是有范围的，超出范围时的数据表示出错。
进位和溢出
- 进位：运算后，最高位向更高位的进位值。
- 溢出：运算结果超出了运算器所能表示的范围。
下列情况就发生了溢出：
8位加法器，运算无符号数，结果 >= 256；
8位加法器，运算有符号数，结果 > +127，<-128；
16位加法器，运算无符号数，结果 >= 65536
16位加法器，运算有符号数，结果 >215-1, <-215
注：某数是无符号数，还是有符号数，其物理意义是由程序员定义。
计算机怎样表示进位和溢出？
最高位的进位值保存在 “进位标志寄存器”（CF） 中。
如加数与被加数的最高位相同，却与结果的最高位相异，则将 “溢出标志寄存器” 置为 1，否则为 0。
程序员如何判断溢出？
如果参与运算的数是无符号数，则看 进位标志（CF），CF = 1，表示溢出错。
如果参与运算的数是有符号数，则看 溢出标志（OF），OF = 1，表示溢出错。
由于进位为 0 ，所以 CF = 0；
由于加数与被加数最高位相同，并且与运算结果的最高位相异，所以 OF = 1；
如果参与的运算的数是无符号数，则正确。
如果参与的运算的数是有符号数，则错误。
由于进位为 1，所以 CF = 1；
由于加数与被加数最高位相同，并且与运算结果的最高位相异，所以 OF = 1；
无论参与的运算数是无符号数还是有符号，由于 CF = 1，OF = 1，结果必然是错误的。