Python计算机视觉 多视图几何——基础矩阵

一、基础矩阵原理

基础矩阵，存在这么一个矩阵F，使得空间中不在两图像平面上的任意点X分别在两图像的投影坐标x,x’满足等式(x’)TFx=0，即x’的转置乘以F，再乘以x的结果为0，那么F就是左边图像到右边图像的基本矩阵，从公式上可以看出基本矩阵是有方向的，右图到左图的基本矩阵就是F的转置。其中，矩阵F为3乘3的矩阵，秩为2。
（PS.转置: 如果 F 是表述点对 (x, x’)之间的基础矩阵, 则 FT 是表述点对 (x’,x)之间的基础矩阵。）
基础矩阵是对极几何的代数表达方式，可以看做是将点投影（转换）为直线，将左影像上的一个点投影到右影像上形成一条核线。

原理

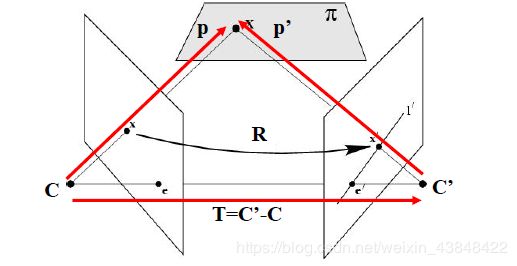
设X在C,C’坐标系中的相对坐标分别为P,P’，则有


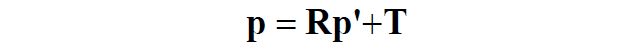
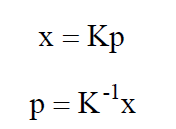
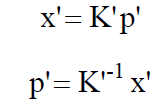
根据三线共面，有


(PS:本质矩阵描述了空间中的点在两个坐标系中的坐标对应关系）
根据前述，K和K’分别为两个相机的内参矩阵，有：

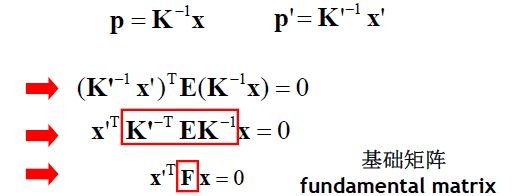
（PS：基础矩阵描述； 空间中的点在两个相平面中的坐标对应关系）

应用
1.简化匹配
2.去除错配特征

二、代码实现

代码实现：

#!/usr/bin/env python
# coding: utf-8

# In[1]:
from PIL import Image
from numpy import *
from pylab import *
import numpy as np
from imp import reload



# In[2]:
import importlib
from PCV.geometry import camera
from PCV.geometry import homography
from PCV.geometry import sfm
from PCV.localdescriptors import sift

camera = importlib.reload(camera)
homography = importlib.reload(homography)
sfm = importlib.reload(sfm)
sift =importlib.reload(sift)


# In[3]:


# Read features
im1 = array(Image.open('image5/1.jpg'))
sift.process_image('image5/1.jpg', 'im1.sift')
l1, d1 = sift.read_features_from_file('im1.sift')

im2 = array(Image.open('image5/2.jpg'))
sift.process_image('image5/2.jpg', 'im2.sift')
l2, d2 = sift.read_features_from_file('im2.sift')


# In[9]:


matches = sift.match_twosided(d1, d2)


# In[10]:


ndx = matches.nonzero()[0]
x1 = homography.make_homog(l1[ndx, :2].T)
ndx2 = [int(matches[i]) for i in ndx]
x2 = homography.make_homog(l2[ndx2, :2].T)

x1n = x1.copy()
x2n = x2.copy()


# In[11]:


print (len(ndx))


# In[12]:


figure(figsize=(16,16))
sift.plot_matches(im1, im2, l1, l2, matches, True)
show()


# In[13]:


# Chapter 5 Exercise 1
# Don't use K1, and K2

#def F_from_ransac(x1, x2, model, maxiter=5000, match_threshold=1e-6):
def F_from_ransac(x1, x2, model, maxiter=5000, match_threshold=1e-6):
    """ Robust estimation of a fundamental matrix F from point
    correspondences using RANSAC (ransac.py from
    http://www.scipy.org/Cookbook/RANSAC).

    input: x1, x2 (3*n arrays) points in hom. coordinates. """

    from PCV.tools import ransac
    data = np.vstack((x1, x2))
    d = 20 # 20 is the original
    # compute F and return with inlier index
    F, ransac_data = ransac.ransac(data.T, model,8, maxiter, match_threshold, d, return_all=True)
    return F, ransac_data['inliers']


# In[15]:


# find E through RANSAC
model = sfm.RansacModel()
F, inliers = F_from_ransac(x1n, x2n, model, maxiter=5000, match_threshold=1e-3)


# In[16]:


print (len(x1n[0]))
print (len(inliers))


# In[17]:


P1 = array([[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0]])
P2 = sfm.compute_P_from_fundamental(F)


# In[18]:


# triangulate inliers and remove points not in front of both cameras
X = sfm.triangulate(x1n[:, inliers], x2n[:, inliers], P1, P2)


# In[19]:


# plot the projection of X
cam1 = camera.Camera(P1)
cam2 = camera.Camera(P2)
x1p = cam1.project(X)
x2p = cam2.project(X)


# In[20]:


figure()
imshow(im1)
gray()
plot(x1p[0], x1p[1], 'o')
#plot(x1[0], x1[1], 'r.')
axis('off')

figure()
imshow(im2)
gray()
plot(x2p[0], x2p[1], 'o')
#plot(x2[0], x2[1], 'r.')
axis('off')
show()


# In[21]:


figure(figsize=(16, 16))
im3 = sift.appendimages(im1, im2)
im3 = vstack((im3, im3))

imshow(im3)

cols1 = im1.shape[1]
rows1 = im1.shape[0]
for i in range(len(x1p[0])):
    if (0<= x1p[0][i]0: #plot([locs1[i][0],locs2[m][0]+cols1],[locs1[i][1],locs2[m][1]],'c')
        
        p1 = array([l1[i][0], l1[i][1], 1])
        p2 = array([l2[m][0], l2[m][1], 1])

       
        
        # Use Sampson distance as error
        Fx1 = dot(F, p1)
        Fx2 = dot(F, p2)
        denom = Fx1[0]**2 + Fx1[1]**2 + Fx2[0]**2 + Fx2[1]**2
        e = (dot(p1.T, dot(F, p2)))**2 / denom
        x1e.append([p1[0], p1[1]])
        x2e.append([p2[0], p2[1]])
        ers.append(e)
x1e = array(x1e)
x2e = array(x2e)
ers = array(ers)


# In[24]:


indices = np.argsort(ers)
x1s = x1e[indices]
x2s = x2e[indices]
ers = ers[indices]
x1s = x1s[:20]
x2s = x2s[:20]


# In[25]:


figure(figsize=(16, 16))
im3 = sift.appendimages(im1, im2)
im3 = vstack((im3, im3))

imshow(im3)

cols1 = im1.shape[1]
rows1 = im1.shape[0]
for i in range(len(x1s)):
    if (0<= x1s[i][0]

实验结果：
室外：
sift特征匹配结果

得到的基础矩阵

恢复这些点的三维位置


修改特征匹配结果后

室内：
在室内实验中，换了好几组图片就都只出现了sift特征匹配的实现，后续的恢复这些点的三维位置和修改特征匹配结果后都没有出现

小结
在实现室外实验的时候，只匹配一组照片就成功得到结果，而在实现室内实验时，匹配了好几组照片都没有实现修改特征匹配后的结果，都只是停留在了sift特征匹配的实现。个人理解，在室内拍摄出来的照片景深落差比较小，影响了特征点的匹配和三维点的恢复，导致结果无法实现。