梯度下降&随即梯度下降
CS299课程的笔记
为什么梯度方向下降最快
方向导数
定义:函数在某一特定方向上的变化率。
方向导数是一个标量,负则函数值该方向减少,正则函数值该方向增加
那么我们想要目标函数值下降,其实是寻找一个方向使得函数变化率的绝对值最大,并且方向为负。
具体如下:

方向导数和偏导数
概念1:方向余弦—在解析几何里,一个向量的三个方向余弦分别是这向量与三个坐标轴之间的角度的余弦。
方向导数能够表示为偏导数和方向余弦和的形式
梯度
从上面可以得到方向导数=(偏导数)*(方向余弦)
就是求偏导数向量和方向余弦的内积何时最大or最小,那么两者的夹角为0orPie

泰勒展开式的证明
从多元泰勒展开得出的证明:参考
批梯度下降
算法
此处是Ng视频的中案例,Alpha为学习速率,参数是全部更新。
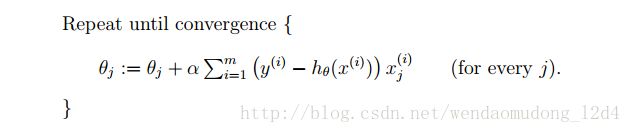
随机梯度
算法
批梯度下降是用所有数据进行参数更新,随即梯度用一个样本数据进行参数更新。
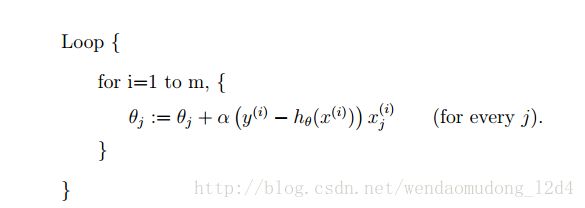
R code
#数据构造
x0 <- rep(1,50)
x1 <- rnorm(50,5,10)
x2 <- rnorm(50,10,10)
x3 <- rnorm(50,15,10)
Epsilon <- rnorm(50,0,1)
y <- 10.8+x1+2.5*x2+5.9*x3+Epsilon
# lm()function used in R --------------------------------------------------
#R软件自带lm函数求解
R_model <- lm(y~x1+x2+x3)
summary(R_model)
#截距项差的比较多,其他的还好吧。并且截距还通过了检验。可能是截距和扰动项相差不大?
#截距项更改之后,效果较好
# Normal Equation ---------------------------------------------------------
X <- as.matrix(cbind(x0,x1,x2,x3))
Y <- as.matrix(y,byrow=F)
Theta1 <- solve(t(X)%*%X)%*%t(X)%*%Y
#result :x0=11.27;x1=0.96;x2=2.48;x3=5.89
#This result is the same to R_model
# Batch Gradient Descent --------------------------------------------------------
#Parameter adjustment:if J is increasing in iteration then make Alpha smaller
J <- c(20,30)
Theta_P <- as.matrix(c(0, 0, 0, 0), byrow = F)
Alpha <- 0.00005
#参数迭代到底是一个一个迭代,还是一次迭代所有参数呢
#参数迭代都是一次全部迭代,想想理论是求梯度呀
#我这里已经是矩阵求导,全部更新
while(abs(J[length(J)]-J[length(J)-1])>0.001){
for (i in 1:4) {
Theta_P[i, 1] <-
Theta_P[i, 1] - (Alpha * (t(X) %*% X %*% Theta_P - t(X) %*% Y))[i, 1]
}
J <- c(J, 0.5 * t(X %*% Theta_P - Y) %*% (X %*% Theta_P - Y))
print(J[length(J)])
if(length(J)>50000){break}
}
#------------------------------------------------------------------------------
while(abs(J[length(J)]-J[length(J)-1])>0.001){
Theta_P <-
Theta_P - (Alpha * (t(X) %*% X %*% Theta_P - t(X) %*% Y))
J <- c(J, 0.5 * t(X %*% Theta_P - Y) %*% (X %*% Theta_P - Y))
print(J[length(J)])
if(length(J)>50000){break}
}
# Stochastic Gradient Descent -------------------------------------------------
#一个样本更新所有的参数,而不是一次只更新一个参数呀
J_r <- c(20, 30)
Theta_P_r <- as.matrix(c(0, 0, 0, 0), byrow = F)
Alpha_r <- 0.00005
while (abs(J_r[length(J_r)] - J_r[length(J_r) - 1]) > 0.001) {
sample_seed <- sample(1:50, 1, replace = F)
for (i in 1:4) {
Theta_P_r[i, 1] <-
Theta_P_r[i, 1] - Alpha_r * X[sample_seed,i ]*(X[sample_seed, ] %*% Theta_P_r -Y[sample_seed, ])
}
J_r <-
c(J_r, 0.5 * t(X %*% Theta_P_r - Y) %*% (X %*% Theta_P_r - Y))
print(J_r[length(J_r)])
if (length(J_r) > 50000) {
break
}
}
#---------------------------------------------------------------------------------
J_r <- c(20, 30)
Theta_P_r <- as.matrix(c(0, 0, 0, 0), byrow = F)
Alpha_r <- 0.00005
while (abs(J_r[length(J_r)] - J_r[length(J_r) - 1]) > 0.001) {
sample_seed <- sample(1:50, 1, replace = F)
Theta_P_r <-
Theta_P_r - Alpha_r * X[sample_seed, ] * (X[sample_seed,] %*% Theta_P_r -
Y[sample_seed,])
J_r <-
c(J_r, 0.5 * t(X %*% Theta_P_r - Y) %*% (X %*% Theta_P_r - Y))
print(J_r[length(J_r)])
if (length(J_r) > 50000) {
break
}
}
#没有梯度下降准确,尤其是截距项。其他项准确度还可以Ref
[1]为什么梯度反方向是函数值下降最快的方向?
[2] 《数学分析》华师三版
Ohters
写博客做笔记还是要有耐心,数学基础还是渣呀。好赖我也是学过数分高代立几的好嘛~然而还是挫的不行。细节还是要搞搞懂,道阻且长,行则将至!


