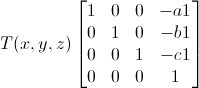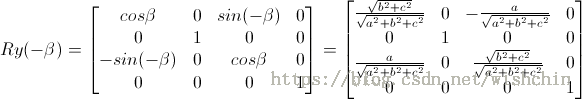三维重建:点绕特定轴旋转公式
一些特定的三维平面运算可以直接在三维空间中进行,也可以在二维平面中运行,通过坐标变化转换到三维空间。旋转方式有中心旋转、轴旋转。
1. 罗德里格旋转公式
在三维旋转理论体系中,罗德里格旋转公式(根据欧林·罗德里格命名)是在给定转轴和旋转角度后,旋转一个向量的有效算法。如果v是在![]() 中的向量,k是转轴的单位向量,θ是旋转角度(根据叉乘的方向确定正负号),那罗德里格旋转公式表达为:
中的向量,k是转轴的单位向量,θ是旋转角度(根据叉乘的方向确定正负号),那罗德里格旋转公式表达为:
![]()
输入:
V = (vx, vy, vz) = (u, v, w),这是待旋转的一个向量。
K = (kx, ky, kz) = (x, y, z),这是单位化后的转轴。
输出:Vrot
计算过程及公式:
Vrot = V cosT + (K * V) sinT + K ( K . V) (1- cosT)
= (u, v, w) cosT + (yw - zv, zu - xw, xv - yu) sinT + (x, y, z)(xu + yv + zw)(1 - cosT)
计算公式:
Vrot.x = u cosT + (yw - zv) sinT + x (xu + yv + zw) ( 1- cosT)
Vrot.y = v cosT + (zu - xw) sinT + y (xu + yv + zw) ( 1- cosT)
Vrot.z = w cosT + (xv - yu) sinT + z (xu + yv + zw) ( 1- cosT)
代码(java版本):
public static Point3d rtRoundLine( Point3d line, Point3d p, double Aplha ){
double u = p.m_x;
double v = p.m_y;
double w = p.m_z;
double T = Aplha;
Point3d axisU = unit( line );
double x= axisU.m_x;
double y= axisU.m_y;
double z= axisU.m_z;
//长度
double l= Math.sqrt(dot(line,line) );
Point3d Vrot = new Point3d();
Vrot.m_x = u *Math.cos(T) + (y * w - z * v) *Math.sin(T) + x *(x * u + y * v + z * w)*( 1- Math.cos(T));
Vrot.m_y = v *Math.cos(T) + (z * u - x * w) *Math.sin(T) + y *(x * u + y * v + z * w)*( 1- Math.cos(T));
Vrot.m_z = w *Math.cos(T) + (x * v - y * u) *Math.sin(T) + z *(x * u + y * v + z * w)*( 1- Math.cos(T));
return Vrot;
}但是罗德里格旋转公式不适用于任意旋转轴旋转,得到的结果是错误的。
二、任意点绕特定轴旋转
参考文章:点绕任意轴旋转....
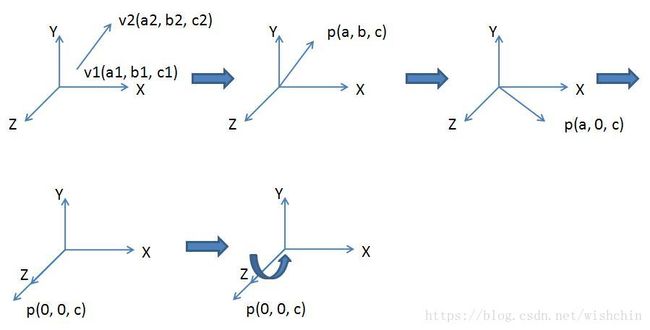
使用通用的把轴转换到Z轴上的方法,经过两次变换和两次逆变换得到旋转矩阵。
如下方法处理:
- 将旋转轴平移至原点
- 将旋转轴旋转至YOZ平面
- 将旋转轴旋转至于Z轴重合
- 绕Z轴旋转θ度
- 执行步骤3的逆过程
- 执行步骤2的逆过程
- 执行步骤1的逆过程
假设用v1(a1, b2, c2)和v2(a2, b2, c2)来表示旋转轴,θ表示旋转角度。为了方便推导,暂时使用右手系并使用列向量,待得出矩阵后转置一下即可,上面步骤对应的流程图如下。
.................................
即
对应的函数代码如下(Java版本):
public static double[][] GetRotMatByLine( Point3d v1, Point3d v2, double theta )
{
int col = 4;
int row = 4;
double[][] pOut= new double[row][col];//一次性完成???
double a = v1.m_x;
double b = v1.m_y;
double c = v1.m_z;
//D3DXVECTOR3 p = *v2 - *v1;
Point3d p = new Point3d(v2.m_x-v1.m_x,v2.m_y-v1.m_y,v2.m_z-v1.m_z);
//D3DXVec3Normalize(&p, &p);
p = unit( p );
double u = p.m_x;
double v = p.m_y;
double w = p.m_z;
double uu = u * u;
double uv = u * v;
double uw = u * w;
double vv = v * v;
double vw = v * w;
double ww = w * w;
double au = a * u;
double av = a * v;
double aw = a * w;
double bu = b * u;
double bv = b * v;
double bw = b * w;
double cu = c * u;
double cv = c * v;
double cw = c * w;
double costheta = Math.cos(theta);
double sintheta = Math.sin(theta);
pOut[0][0] = uu + (vv + ww) * costheta;
pOut[0][1] = uv * (1 - costheta) + w * sintheta;
pOut[0][2] = uw * (1 - costheta) - v * sintheta;
pOut[0][3] = 0;
pOut[1][0] = uv * (1 - costheta) - w * sintheta;
pOut[1][1] = vv + (uu + ww) * costheta;
pOut[1][2] = vw * (1 - costheta) + u * sintheta;
pOut[1][3] = 0;
pOut[2][0] = uw * (1 - costheta) + v * sintheta;
pOut[2][1] = vw * (1 - costheta) - u * sintheta;
pOut[2][2] = ww + (uu + vv) * costheta;
pOut[2][3] = 0;
pOut[3][0] = (a * (vv + ww) - u * (bv + cw)) * (1 - costheta) + (bw - cv) * sintheta;
pOut[3][1] = (b * (uu + ww) - v * (au + cw)) * (1 - costheta) + (cu - aw) * sintheta;
pOut[3][2] = (c * (uu + vv) - w * (au + bv)) * (1 - costheta) + (av - bu) * sintheta;
pOut[3][3] = 1;
return pOut;
}//GetRotMatByLine使用函数的代码:
public static Point3d rtRoundLine( Point3d ps, Point3d pe, Point3d p, double Aplha,double[][] transM ){
//计算旋转点
Point3d Vrot = new Point3d();
//点乘矩阵
if( true ){
Vrot.m_x = p.m_x* transM[0][0] +p.m_y* transM[1][0] +p.m_z* transM[2][0]+ transM[3][0];
Vrot.m_y = p.m_x* transM[0][1] +p.m_y* transM[1][1] +p.m_z* transM[2][1]+ transM[3][1];
Vrot.m_z = p.m_x* transM[0][2] +p.m_y* transM[1][2] +p.m_z* transM[2][2]+ transM[3][2];
}
Vrot.m_z =-Vrot.m_z;
return Vrot;
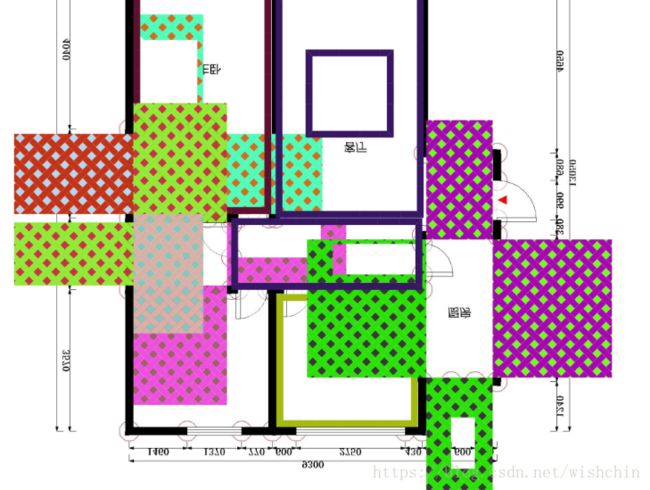
}示例结果:
点云图与平面图对比
参考:各种旋转方式总结.....
罗德里格旋转公式....