计算机视觉学习11_图片分割_图割法(Graph Cut)
文章目录
- 最大流最小割
- Graph Cut(图割算法)
- 最大流最小割-代码实现
- 图片前后景分割-代码实现
最大流最小割
参考博客 https://www.cnblogs.com/dyzll/p/5887266.html
最大流
给定指定的一个有向图,其中有两个特殊的点源S(Sources)和汇T(Sinks),每条边有指定的容量(Capacity),求满足条件的从S到T的最大流(MaxFlow)。
最小割
割是网络中定点的一个划分,它把网络中的所有顶点划分成两个顶点集合S和T,其中源点s∈S,汇点t∈T。记为CUT(S,T),满足条件的从S到T的最小割(Min cut)。
![]()
可以计算出对于这两种情况净流f(S,T)等于19。
一个直观的解释是:根据网络流的定义,只有源点s会产生流量,汇点t会接收流量。因此任意非s和t的点u,其净流量一定为0,也即是Σ(f(u,v))=0。而源点s的流量最终都会通过割(S,T)的边到达汇点t,所以网络流的流f等于割的静流f(S,T)。
对于一个网络流图G=(V,E),其中有源点s和汇点t,那么下面三个条件是等价的:
流f是图G的最大流
残留网络Gf不存在增广路
对于G的某一个割(S,T),此时f = C(S,T)
找到最小割后,沿最小割进行分割,可以得到比较好的效果。
Graph Cut(图割算法)
参考博客:https://blog.csdn.net/zouxy09/article/details/8532111
此类方法把图像分割问题与图的最小割(min cut)问题相关联。首先用一个无向图G=
第一种顶点和边是:第一种普通顶点对应于图像中的每个像素。每两个邻域顶点(对应于图像中每两个邻域像素)的连接就是一条边。这种边也叫n-links。
第二种顶点和边是:除图像像素外,还有另外两个终端顶点,叫S(source:源点,取源头之意)和T(sink:汇点,取汇聚之意)。每个普通顶点和这2个终端顶点之间都有连接,组成第二种边。这种边也叫t-links。

上图就是一个图像对应的s-t图,每个像素对应图中的一个相应顶点,另外还有s和t两个顶点。上图有两种边,实线的边表示每两个邻域普通顶点连接的边n-links,虚线的边表示每个普通顶点与s和t连接的边t-links。在前后景分割中,s一般表示前景目标,t一般表示背景。
图中每条边都有一个非负的权值we,也可以理解为cost(代价或者费用)。一个cut(割)就是图中边集合E的一个子集C,那这个割的cost(表示为|C|)就是边子集C的所有边的权值的总和。
Graph Cuts中的Cuts是指这样一个边的集合,很显然这些边集合包括了上面2种边,该集合中所有边的断开会导致残留”S”和”T”图的分开,所以就称为“割”。如果一个割,它的边的所有权值之和最小,那么这个就称为最小割,也就是图割的结果。而福特-富克森定理表明,网路的最大流max flow与最小割min cut相等。所以由Boykov和Kolmogorov发明的max-flow/min-cut算法就可以用来获得s-t图的最小割。这个最小割把图的顶点划分为两个不相交的子集S和T,其中s ∈S,t∈ T和S∪T=V 。这两个子集就对应于图像的前景像素集和背景像素集,那就相当于完成了图像分割。
也就是说图中边的权值就决定了最后的分割结果,那么这些边的权值怎么确定呢?
图像分割可以看成pixel labeling(像素标记)问题,目标(s-node)的label设为1,背景(t-node)的label设为0,这个过程可以通过最小化图割来最小化能量函数得到。那很明显,发生在目标和背景的边界处的cut就是我们想要的(相当于把图像中背景和目标连接的地方割开,那就相当于把其分割了)。同时,这时候能量也应该是最小的。假设整幅图像的标签label(每个像素的label)为L= {l1,l2, lp },其中li为0(背景)或者1(目标)。那假设图像的分割为L时,图像的能量可以表示为:
E(L)=aR(L)+B(L)
其中,R(L)为区域项(regional term),B(L)为边界项(boundary term),而a就是区域项和边界项之间的重要因子,决定它们对能量的影响大小。如果a为0,那么就只考虑边界因素,不考虑区域因素。E(L)表示的是权值,即损失函数,也叫能量函数,图割的目标就是优化能量函数使其值达到最小。
区域项:

其中Rp(lp)表示为像素p分配标签lp的惩罚,Rp(lp)能量项的权值可以通过比较像素p的灰度和给定的目标和前景的灰度直方图来获得,换句话说就是像素p属于标签lp的概率,我希望像素p分配为其概率最大的标签lp,这时候我们希望能量最小,所以一般取概率的负对数值,故t-link的权值如下:
Rp(1) = -ln Pr(Ip|’obj’); Rp(0) = -ln Pr(Ip|’bkg’)
由上面两个公式可以看到,当像素p的灰度值属于目标的概率Pr(Ip|’obj’)大于背景Pr(Ip|’bkg’),那么Rp(1)就小于Rp(0),也就是说当像素p更有可能属于目标时,将p归类为目标就会使能量R(L)小。那么,如果全部的像素都被正确划分为目标或者背景,那么这时候能量就是最小的。
边界项:
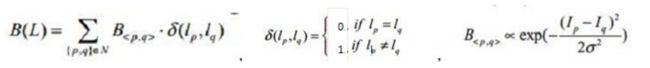
其中,p和q为邻域像素,边界平滑项主要体现分割L的边界属性,B
总结:
我们目标是将一幅图像分为目标和背景两个不相交的部分,我们运用图分割技术来实现。首先,图由顶点和边来组成,边有权值。那我们需要构建一个图,这个图有两类顶点,两类边和两类权值。普通顶点由图像每个像素组成,然后每两个邻域像素之间存在一条边,它的权值由上面说的“边界平滑能量项”来决定。还有两个终端顶点s(目标)和t(背景),每个普通顶点和s都存在连接,也就是边,边的权值由“区域能量项”Rp(1)来决定,每个普通顶点和t连接的边的权值由“区域能量项”Rp(0)来决定。这样所有边的权值就可以确定了,也就是图就确定了。这时候,就可以通过min cut算法来找到最小的割,这个min cut就是权值和最小的边的集合,这些边的断开恰好可以使目标和背景被分割开,也就是min cut对应于能量的最小化。而min cut和图的max flow是等效的,故可以通过max flow算法来找到s-t图的min cut。目前的算法主要有:
-
Goldberg-Tarjan
-
Ford-Fulkerson
-
上诉两种方法的改进算法
权值:
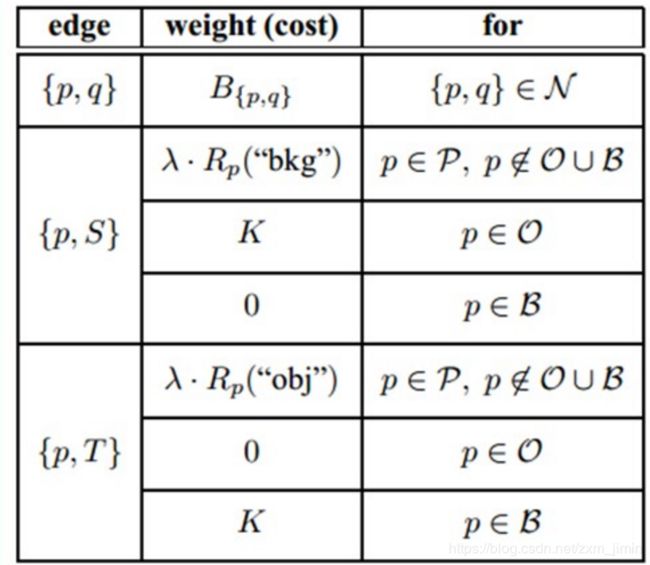
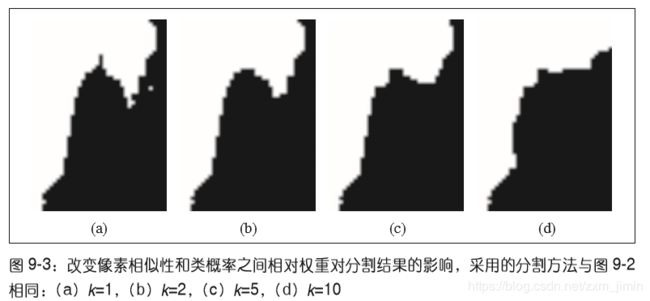
Graph cut的3x3图像分割示意图:我们取两个种子点(就是人为的指定分别属于目标和背景的两个像素点),然后我们建立一个图,图中边的粗细表示对应权值的大小,然后找到权值和最小的边的组合,也就是(c)中的cut,即完成了图像分割的功能。

最大流最小割-代码实现
from pygraph.classes.digraph import digraph
from pygraph.algorithms.minmax import maximum_flow
gr = digraph()
gr.add_nodes([0,1,2,3])
gr.add_edge((0,1), wt=4)
gr.add_edge((1,2), wt=3)
gr.add_edge((2,3), wt=5)
gr.add_edge((0,2), wt=3)
gr.add_edge((1,3), wt=4)
flows,cuts = maximum_flow(gr, 0, 3)
print ('flow is:' , flows)
print ('cut is:' , cuts)
图片前后景分割-代码实现
from pylab import *
from numpy import *
from pygraph.classes.digraph import digraph
from pygraph.algorithms.minmax import maximum_flow
from PCV.classifiers import bayes
"""
Graph Cut image segmentation using max-flow/min-cut.
"""
def build_bayes_graph(im,labels,sigma=1e2,kappa=1):
""" Build a graph from 4-neighborhood of pixels.
Foreground and background is determined from
labels (1 for foreground, -1 for background, 0 otherwise)
and is modeled with naive Bayes classifiers.
"""
""" 从像素四邻域建立一个图,前景和背景(前景用 1 标记,背景用 -1 标记, 其他的用 0 标记)由 labels 决定,并用朴素贝叶斯分类器建模 """
m,n = im.shape[:2]
# RGB vector version (one pixel per row)
# 每行是一个像素的 RGB 向量
vim = im.reshape((-1,3))
# RGB for foreground and background
# 前景和背景(RGB)
foreground = im[labels==1].reshape((-1,3))
background = im[labels==-1].reshape((-1,3))
train_data = [foreground,background]
# train naive Bayes classifier
# 训练朴素贝叶斯分类器
bc = bayes.BayesClassifier()
bc.train(train_data)
# get probabilities for all pixels
# 获取所有像素的概率
bc_lables,prob = bc.classify(vim)
prob_fg = prob[0]
prob_bg = prob[1]
# create graph with m*n+2 nodes
# 用m * n +2 个节点创建图 除所有像素点外加上原点和汇点
gr = digraph()
gr.add_nodes(range(m*n+2))
source = m*n # second to last is source
sink = m*n+1 # last node is sink
# normalize
# 归一化
for i in range(vim.shape[0]):
vim[i] = vim[i] / (linalg.norm(vim[i]) + 1e-9)
# go through all nodes and add edges
# 遍历所有的节点,并添加边
for i in range(m*n):
# add edge from source
# 从源点添加边
gr.add_edge((source,i), wt=(prob_fg[i]/(prob_fg[i]+prob_bg[i])))
# add edge to sink
# 向汇点添加边
gr.add_edge((i,sink), wt=(prob_bg[i]/(prob_fg[i]+prob_bg[i])))
# add edges to neighbors
# 向相邻节点添加边
if i%n != 0: # left exists # 左边存在
edge_wt = kappa*exp(-1.0*sum((vim[i]-vim[i-1])**2)/sigma)
gr.add_edge((i,i-1), wt=edge_wt)
if (i+1)%n != 0: # right exists
edge_wt = kappa*exp(-1.0*sum((vim[i]-vim[i+1])**2)/sigma)
gr.add_edge((i,i+1), wt=edge_wt)
if i//n != 0: # up exists
edge_wt = kappa*exp(-1.0*sum((vim[i]-vim[i-n])**2)/sigma)
gr.add_edge((i,i-n), wt=edge_wt)
if i//n != m-1: # down exists
edge_wt = kappa*exp(-1.0*sum((vim[i]-vim[i+n])**2)/sigma)
gr.add_edge((i,i+n), wt=edge_wt)
return gr
def cut_graph(gr,imsize):
""" Solve max flow of graph gr and return binary
labels of the resulting segmentation."""
""" 用最大流对图 gr 进行分割,并返回分割结果的二值标记 """
m,n = imsize
source = m*n # second to last is source # 倒数第二个节点是源点
sink = m*n+1 # last is sink# 倒数第已个节点是汇点
# cut the graph
# 对图进行分割
flows,cuts = maximum_flow(gr,source,sink)
# convert graph to image with labels
# 将图转为带有标记的图像
res = zeros(m*n)
for pos,label in list(cuts.items())[:-2]: #don't add source/sink # 不要添加源点 / 汇点
res[pos] = label
return res.reshape((m,n))
def save_as_pdf(gr,filename,show_weights=False):
from pygraph.readwrite.dot import write
import gv
dot = write(gr, weighted=show_weights)
gvv = gv.readstring(dot)
gv.layout(gvv,'fdp')
gv.render(gvv,'pdf',filename)
def show_labeling(im,labels):
""" Show image with foreground and background areas.
labels = 1 for foreground, -1 for background, 0 otherwise."""
imshow(im)
contour(labels,[-0.5,0.5])
contourf(labels,[-1,-0.5],colors='b',alpha=0.25)
contourf(labels,[0.5,1],colors='r',alpha=0.25)
#axis('off')
xticks([])
yticks([])
实现前后景分割
# -*- coding: utf-8 -*-
from scipy.misc import imresize
from PCV.tools import graphcut
from PIL import Image
from numpy import *
from pylab import *
im = array(Image.open("empire.jpg"))
im = imresize(im, 0.07)
size = im.shape[:2]
# add two rectangular training regions
labels = zeros(size)
labels[3:18, 3:18] = -1
labels[-18:-3, -18:-3] = 1
# create graph
g = graphcut.build_bayes_graph(im, labels, kappa=1)
# cut the graph
res = graphcut.cut_graph(g, size)
figure()
graphcut.show_labeling(im, labels)
figure()
imshow(res)
gray()
axis('off')
show()