计算机组成与体系结构(2)
- Cache概念
- 主存-分类
- 磁盘结构与参数
- 系统可靠性分析-串联系统和并联系统
- 差错控制-CRC 与海明校验码
·
·
- Cache概念
Cache的功能:提高CPU数据输入输出的速度,突破冯·诺依曼瓶颈,即CPU与存储系统间数据传送带宽限制
在计算机的存储系统体系中,Cache是访问速度最快的层次
使用Cache改善系统性能的依据是程序的局部性原理
考题:若问下列寄存器中最快的是?
若有寄存器,则选寄存器,若没有寄存器的选项,就要考虑选Cache
【例题:
h 为Cache 的访问命中率 95%
t1:Cache 的周期时间 1ns
t2:主存储器的周期时间 1ms = 1000ns
以读操作为例
使用“Cache + 主存储器”的系统的平均周期为t3
t3 = h * t1 + (1 - h) * t2 注:(1-h)为失效率,即未命中率
= 95% * 1ns + (1 - 95%) * 1000ns
= 0.95ns + 50ns
= 50.95ns
相比于单独用主存储器访问,时间节省了将近20倍(1000ns / 50.95ns )】
·
·
- 主存-分类
分为:随机存取存储器和只读存储器
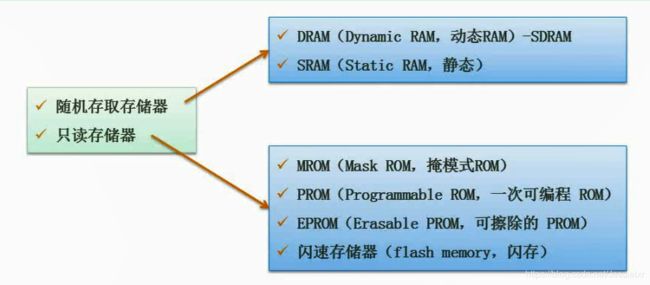
主存的编址
8*4位的存储器
表示8个地址空间,每个地址空间上存储4个比特位的信息
·
·
-磁盘结构与参数
存取时间= 寻道时间 + 等待时间(平均定位时间 + 转动延迟)
注意:寻道时间是指磁头移动到磁道所需的时间;需等待时间为等待读写的扇区转到磁头下方所用的时间。
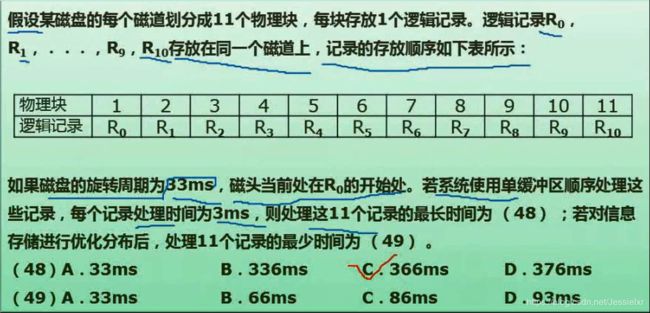
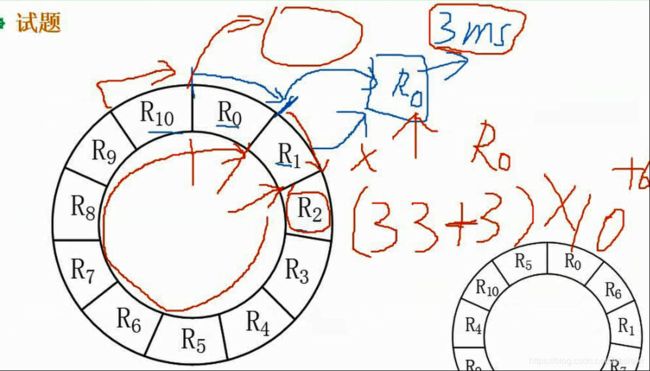
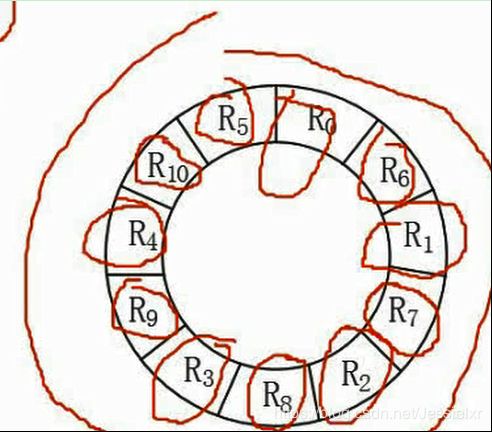
读取一个记录并处理的时间是6ms,读取R0并处理后,指针到达R1的末尾,因此后面的每一条记录都需要增加读取处理时间,即
每一个记录读取并处理的时间都是(33+3)
从R0 到R9都是这样,因此R0 到R9所花时间为(33+3)*10
最后R10读取记录并处理的时间为6ms,因此最终处理这11个记录的最长时间为(33+3)*10 + 6=366ms
如果为了使得处理时间最短,则上图能够很好地实现,每隔一个空放一个相邻记录,这样处理时间大大减少了,也就是每个记录的处理时间都是6ms,一共11个记录,最少的处理时间为 6*11= 66
·
·
- 系统可靠性分析-串联系统和并联系统
串联系统:所有子系统都必须正常运行,有一个无法运行,整个大的系统都无法正常运行

R代表可靠度,可靠度相乘,求出整个系统的总可靠度
λ是失效率,进行累加
如果单个系统的失效率是0.1,就不好用失效率的公式了,反而会越加越大,所以失效率公式(近似公式)的使用建立在子系统比较多,且失效率极低的时候将失效率累加,便于快速算出失效率
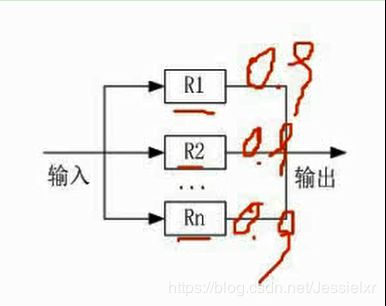
并联模型:有一个子系统能正常运行,整个系统都能正常运行;只有当所有子系统同时失效时,整个系统才失效。
可靠度:R= 1 - (1-R1)× (1-R2)× …×(1-Rn)
可靠度: (1-0.9)的三次方,再用1-(1-0.9)的三次方
但此种方法比较复杂
`
`
- 差错控制-CRC 与海明校验码
(1)循环校验码CRC
一种可以做检错,但不能做纠错的编码
也叫:模2除法

模二除法:核心:异或操作:
1和0异或得到1,0和1异或得到1,1和1异或就得到0
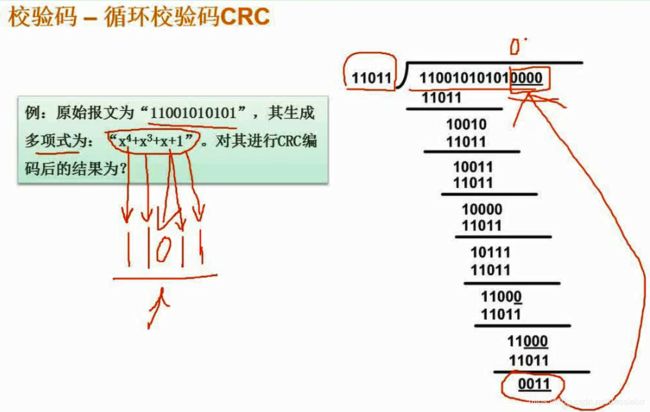
如图中,11001010101,生成多项式是五位,这里具体它为什么是11011不明白,但这个算法的核心就是异或,异或结果是0011,把0011加在11001010101末尾,再用110010101010011进行模二除法,能够整除
这个110010101010011就是CRC编码
(2)海明校验码
校验位的位置是位于整个完成的信息编码的2的n次方位
设数据为01101001,试采用校验位求其偶校验方式的海明码。
(1)确定数据位D和校验位P在海明码中的位置:
由海明码编码规则可知:
pi在海明码的第2i-1
比如P4=2^(4-1)=8,所以位于第8位

(2)确定校验关系
这个难点在于如何确定校验位组。
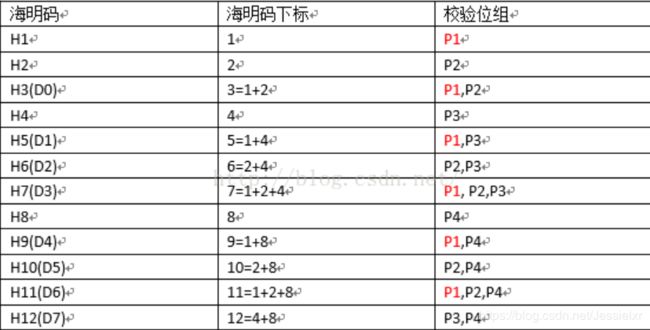
举一个例子来说:H3=D0,海明码下标为3,我们必须用已知的校验位所对应的海明码下标(P1,P2,P3,P4,它们的海明码下标分别是 1,2,4,8)来表示3,这里3就可以等于1+2。
H5为什么是1+4而不是2+3呢?因为H3不是校验位,是数据位。
比如P1 的校验位为表格中红色标记出来所对应的海明码的位数
故:P1校验:P1,D0,D1,D3,D4,D6
P1=D0⊕D1⊕D3⊕D4⊕D6=1⊕0⊕1⊕0⊕1=1
⊕符号:代表异或,相同则为0,不同则为1。只要仔细一定可以计算正确。
P2、P3、P4的海明码计算也是如此,关键是要找出正确的校验位组,所以海明校验码:011001001101