算法竞赛专题解析（6）：搜索进阶(1)--搜索基础

本系列文章将于2021年整理出版，书名《算法竞赛专题解析》。
前驱教材：《算法竞赛入门到进阶》 清华大学出版社 2019.8
网购：京东 当当      作者签名书

如有建议，请加QQ 群：567554289，或联系作者QQ：15512356

  《算法竞赛入门到进阶》的第4章“搜索技术”，讲解了递归、BFS、DFS的原理，以及双向广搜、A*算法、剪枝、迭代加深搜索、IDA*的经典例题，适合入门搜索算法。（第4章“搜索技术”电子版下载： https://github.com/luoyongjun999/code 其中的补充资料）
  本文将分几篇专题介绍搜索扩展内容、讲解更多习题，便于读者深入掌握搜索技术。
  第1篇：搜索基础。
  第2篇：剪枝。
  第3篇～：双向广搜、迭代加深、A*搜索等。
  本文是第1篇。

1 搜索简介

  搜索，就是查找解空间，它是“暴力法”算法思想的具体实现。
  暴力法（Brute force，又译为蛮力法）：把所有可能的情况都罗列出来，然后逐一检查，从中找到答案。这种方法简单、直接，不玩花样，利用了计算机强大的计算能力。
  搜索是“通用”的方法。一个问题，如果比较难，那么先尝试一下搜索，或许能启发出更好的算法。竞赛的时候，遇到不会的难题，如果有时间，就用搜索提交一下，说不定判题数据很弱，就通过了。
搜索的思路很简单，但是操作起来也并不容易。一般有以下操作：
  （1）找到所有可能的数据，并且用数据结构表示和存储。常用的搜索算法是BFS和DFS。
  （2）优化。尽量多地排除不符合条件的数据，以减少搜索的空间。
  （3）用某个算法快速检索这些数据。

2 搜索算法的基本思路

  搜索的基本算法是：深度优先搜索（DFS, Depth-First Search）、宽度优先搜索（BFS, Breadth-First Search，或称为广度优先搜索）。
  这两个算法的思想，用老鼠走迷宫的例子来说明，又形象又透彻。
  迷宫内部的路错综复杂，老鼠从入口进去后，怎么才能找到出口？有两种不同的方法：
  （1）一只老鼠走迷宫。它在每个路口，都选择先走右边（当然，选择先走左边也可以），能走多远就走多远；直到碰壁无法再继续往前走，然后往回退一步，这一次走左边，然后继续往下走。用这个办法，能走遍所有的路，而且不会重复（回退不算重复走）。这个思路，就是DFS。
  （2）一群老鼠走迷宫。假设老鼠是无限多的，这群老鼠进去后，在每个路口，都派出部分老鼠探索所有没走过的路。走某条路的老鼠，如果碰壁无法前行，就停下；如果到达的路口已经有别的老鼠探索过了，也停下。很显然，所有的道路都会走到，而且不会重复。这个思路，就是BFS。BFS看起来像“并行计算”，不过，由于程序是单机顺序运行的，所以，可以把BFS看成是并行计算的模拟。
  简洁地说：BFS是“逐层扩散”，DFS是“一路到底、逐层回退”。
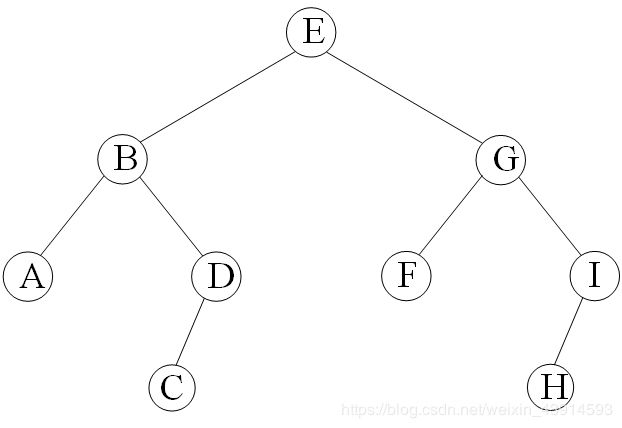
  下面用一棵二叉树为例子，演示BFS和DFS的访问顺序。

图1 一棵二叉树

  （1）BFS的访问顺序是：{E B G A D F I C H}，即“第1层E–第2层BG–第3层ADFI–第4层CH”。
  （2）DFS的访问顺序，设先访问左节点，后访问右节点，那么访问顺序是：{E B A D C G F I H}。需要注意的是，访问顺序不是输出顺序。例如上面的二叉树，它的中序遍历、先序遍历、后序遍历都不同，但是对节点的访问顺序是一样的（实际上就是先序遍历）。具体操作，见下一节的代码。

3 BFS的性质和代码实现

  BFS和DFS的实现：“BFS=队列”，“DFS=递归”。
  为什么“BFS=队列”呢？以老鼠走迷宫为例，从起点s开始，一层一层地扩散出去。处理完离s近的第i层之后，再处理第i+1层。这一操作用队列最方便，处理第i层的节点a时，把a的第i+1层的邻居，放到队列尾部即可。
  队列内的节点有2个特征：
  （1）处理完第i层后，才会处理第i+1层；
  （2）队列中最多有2层节点，其中第i层节点都在第i+1层前面。
  下面给出BFS遍历图1二叉树的代码。分别给出了静态版和指针版二叉树的代码，竞赛中一般用静态版二叉树，不易出错。两个代码都使用STL的queue队列。
  两个代码的输出都是：E B G A D F I C H。

BFS（静态版二叉树）

#include 
using namespace std;
const int maxn = 100005;
struct Node{                  //静态二叉树
    char value;
    int lchild, rchild;    
}node[maxn];

int index = 0;                 //记录节点
int newNode(char val){
	node[index].value = val;
	node[index].lchild = -1;   //-1表示空
	node[index].rchild = -1;
	return index ++;
}
void insert(int &father, int child, int l_r){     //插入孩子
	if(l_r == 0)              //左孩子
		node[father].lchild = child;
	else                      //右孩子
		node[father].rchild = child;	
}
int buildtree(){              //建一棵二叉树
    int A = newNode('A');int B = newNode('B');int C = newNode('C');
    int D = newNode('D');int E = newNode('E');int F = newNode('F');
    int G = newNode('G');int H = newNode('H');int I = newNode('I');
    insert(E,B,0);  insert(E,G,1);       //E的左孩子是B，右孩子是G
    insert(B,A,0);  insert(B,D,1);
    insert(G,F,0);  insert(G,I,1);
    insert(D,C,0);  insert(I,H,0);
    int root = E;
    return root;
}
int main(){   
    int root = buildtree();
    queue <int> q;        
    q.push(root);                          //从根节点开始
    while(q.size()){
        int tmp = q.front();  
        cout << node[tmp].value << " ";    //打印队头
        q.pop();                           //去掉队头
        if(node[tmp].lchild != -1) q.push(node[tmp].lchild);   //左孩子入队
        if(node[tmp].rchild != -1) q.push(node[tmp].rchild);   //右孩子入队     
    }
    return 0;
}

  作为对照，下面给出指针版二叉树代码。

BFS（指针版二叉树）

#include 
using namespace std;

struct node{                         //指针二叉树
    char value;
    node *l, *r;
    node(char value = '#', node *l = NULL, node *r = NULL):value(value), l(l), r(r){}
};
void remove_tree(node *root){         //释放空间
    if(root == NULL) return;
    remove_tree(root->l);
    remove_tree(root->r);
    delete root;
}
int main(){
    node  *A,*B,*C,*D,*E,*F,*G,*H,*I;             //以下建一棵二叉树
    A = new node('A'); B = new node('B'); C = new node('C'); 
    D = new node('D'); E = new node('E'); F = new node('F'); 
    G = new node('G'); H = new node('H'); I = new node('I');
    E->l = B; E->r = G;      B->l = A; B->r = D;
    G->l = F; G->r = I;      D->l = C; I->l = H;   //以上建了一棵二叉树

    queue <node> q;               
    q.push(*E);
    while(q.size()){
        node *tmp;
        tmp = &(q.front());  
        cout << tmp->value << " ";            //打印队头
        q.pop();                              //去掉队头
        if(tmp->l) q.push(*(tmp->l));         //左孩子入队
        if(tmp->r) q.push(*(tmp->r));         //右孩子入队
    }
    remove_tree(E); 
    return 0;
}

  BFS是逐层扩散的，非常符合在图上计算最短路径，先扩散到的节点，离根节点更近。很多最短路径算法，都是在BFS上发展出来的。
  具体内容，请参考《算法竞赛入门到进阶》第10章图论。

4 DFS的常见操作和代码实现

4.1 DFS的常见操作

  DFS的原理，就是递归的过程。
  DFS的代码比BFS更简短一些。下面给出两个代码，分别基于指针版和静态版二叉树。它们输出了图1二叉树的各种DFS操作，有时间戳、DFS序、树深度、子树节点数，另外还给出了二叉树的中序输出、先序输出、后序输出。
  DFS访问节点，经常用到以下操作：
  （1）节点第一次被访问的时间戳。用dfn[i]表示节点i第一次被访问的时间戳，函数dfn_order()打印出了时间戳：
    dfn[E]=1; dfn[B]=2; dfn[A]=3; dfn[D]=4; dfn[C]=5;
    dfn[G]=6; dfn[F]=7; dfn[I]=8; dfn[H]=9。
  时间戳就是先序输出。
  （2）DFS序。在递归时，每个节点会来回访问2次，即第1次访问和第2次回溯。函数visit_order()打印出了DFS序：
    {E B A A D C C D B G F F I H H I G E}
  这个序列有一个重要特征：每个节点出现2次，被这2次包围起来的，是以它为父节点的一棵子树。例如序列中的{B A A D C C D B}，就是B为父节点的一棵子树，又例如{I H H I}，是以I为父节点的一棵子树。这个特征是递归操作产生的。
  （3）树的深度。从根节点往子树DFS，每个节点第一次被访问时，深度加1，从这个节点回溯时，深度减1。用deep[i]表示节点i的深度，函数deep_node()打印出了深度：
    deep[E]=1; deep[B]=2; deep[A]=3; deep[D]=3; deep[C]=4;
    deep[G]=2; deep[F]=3; deep[I]=3; deep[H]=4。
  （4）子树节点总数。用num[i]表示以i为父亲的子树上的节点总数，例如，以B为父节点的子树，共有4个节点{A B C D}。只需要简单地DFS一次就能完成，每个节点的数量等于它的2个子树的数量相加，再加1，即加它自己。函数num_node()做了计算并打印出了以每个节点为父亲的子树上的节点数量。
  另外还有树的重心：在一棵中，找到一个节点，把树变为以该点为根的有根树，并且最大子树的结点数最小。本文没有给出代码。
  竞赛中一般用静态版二叉树写代码。作为对照，后面也给出指针版二叉树的代码。

DFS（静态版二叉树）

#include 
using namespace std;
const int maxn = 100005;

struct Node{
    char value;
    int lchild, rchild;    
}node[maxn];

int index = 0;                 //记录节点
int newNode(char val){         //新建节点
	node[index].value = val;
	node[index].lchild = -1;   //-1表示空
	node[index].rchild = -1;
	return index ++;
}
void insert(int &father, int child, int l_r){   //插入孩子
	if(l_r == 0)              //左孩子
		node[father].lchild = child;
	else                      //右孩子
		node[father].rchild = child;	
}
int dfn[maxn] = {0};              //dfn[i]是节点i的时间戳
int dfn_timer = 0;
void dfn_order (int father){      
    if(father != -1){
        dfn[father] = ++dfn_timer; 
        printf("dfn[%c]=%d; ", node[father].value, dfn[father]);    
                                    //打印访问节点的时间戳
        dfn_order (node[father].lchild);
        dfn_order (node[father].rchild);        
    }
}
int visit_timer = 0;     
void visit_order (int father){        //打印DFS序
    if(father != -1){
        printf("visit[%c]=%d; ", node[father].value, ++visit_timer);  
                                      //打印DFS序：第1次访问节点 
        visit_order (node[father].lchild);
        visit_order (node[father].rchild);
        printf("visit[%c]=%d; ", node[father].value, ++visit_timer);  
                                      //打印DFS序：第2次回溯
    }
}
int deep[maxn] = {0};                 //deep[i]是节点i的深度
int deep_timer = 0;         
void deep_node (int father){      
    if(father != -1){
        deep[father] = ++deep_timer; 
        printf("deep[%c]=%d; ",node[father].value,deep[father]);    
                                      //打印树的深度，第一次访问时，深度+1 
        deep_node (node[father].lchild);
        deep_node (node[father].rchild);
        deep_timer--;                 //回溯时，深度-1
    }
}
int num[maxn] = {0};        //num[i]是以i为父亲的子树上的节点总数
int num_node (int father){          
    if(father == -1)  return 0;
    else{
        num[father] = num_node (node[father].lchild) + 
                      num_node (node[father].rchild) + 1; 
        printf("num[%c]=%d; ", node[father].value, num[father]); //打印数量
        return num[father];
    }
}
void preorder (int father){                 //求先序序列
    if(father != -1){
        cout << node[father].value <<" ";   //先序输出
        preorder (node[father].lchild);
        preorder (node[father].rchild);
    }
}
void inorder (int father){                   //求中序序列
    if(father != -1){
        inorder (node[father].lchild);;
        cout << node[father].value <<" ";    //中序输出
        inorder (node[father].rchild);
    }
}
void postorder (int father){                 //求后序序列
    if(father != -1){
        postorder (node[father].lchild);;
        postorder (node[father].rchild);
        cout << node[father].value <<" ";    //后序输出
    }
}
int buildtree(){                             //建一棵树
    int A = newNode('A');int B = newNode('B');int C = newNode('C');
    int D = newNode('D');int E = newNode('E');int F = newNode('F');
    int G = newNode('G');int H = newNode('H');int I = newNode('I');
    insert(E,B,0);  insert(E,G,1);         //E的左孩子是B，右孩子是G
    insert(B,A,0);  insert(B,D,1);
    insert(G,F,0);  insert(G,I,1);
    insert(D,C,0);  insert(I,H,0);
    int root = E;
    return root;
}
int main(){
    int root = buildtree();
    cout <<"dfn order: ";     dfn_order(root); cout <<endl;     //打印时间戳
    cout <<"visit order: "; visit_order(root); cout <<endl;     //打印DFS序
    cout <<"deep order: ";    deep_node(root); cout <<endl;     //打印节点深度
    cout <<"num of tree: ";    num_node(root); cout <<endl;  //打印子树上的节点数
    cout <<"in order:   ";      inorder(root); cout << endl;    //打印中序序列
    cout <<"pre order:  ";     preorder(root); cout << endl;    //打印先序序列
    cout <<"post order: ";    postorder(root); cout << endl;    //打印后序序列
    return 0;
}
/*输出是：
dfn order: dfn[E]=1; dfn[B]=2; dfn[A]=3; dfn[D]=4; dfn[C]=5; dfn[G]=6; dfn[F]=7; dfn[I]=8; dfn[H]=9;
visit order: visit[E]=1; visit[B]=2; visit[A]=3; visit[A]=4; visit[D]=5; visit[C]=6; visit[C]=7; visit[D]=8; visit[B]=9; visit[G]=10; visit[F]=11; visit[F]=12; visit[I]=13; visit[H]=14; visit[H]=15; visit[I]=16; visit[G]=17; visit[E]=18;
deep order: deep[E]=1; deep[B]=2; deep[A]=3; deep[D]=3; deep[C]=4; deep[G]=2; deep[F]=3; deep[I]=3; deep[H]=4;
num of tree: num[A]=1; num[C]=1; num[D]=2; num[B]=4; num[F]=1; num[H]=1; num[I]=2; num[G]=4; num[E]=9;
in order:   A B C D E F G H I
pre order:  E B A D C G F I H
post order: A C D B F H I G E
*/

DFS（指针版二叉树）

#include 
using namespace std;

struct node{
    char value;
    node *l, *r;
    node(char value = '#', node *l = NULL, node *r = NULL):value(value), l(l), r(r){}
};
void preorder (node *root){          //求先序序列
    if(root != NULL){
        cout << root->value <<" ";   //先序输出
        preorder (root ->l);
        preorder (root ->r);
    }
}
void inorder (node *root){           //求中序序列
    if(root != NULL){
        inorder (root ->l);
        cout << root->value <<" ";   //中序输出
        inorder (root ->r);
    }
}
void postorder (node *root){          //求后序序列
    if(root != NULL){
        postorder (root ->l);
        postorder (root ->r);
        cout << root->value <<" ";    //后序输出
    }
}
void remove_tree(node *root){         //释放空间
    if(root == NULL) return;
    remove_tree(root->l);
    remove_tree(root->r);
    delete root;
}
int main(){
    node  *A, *B,*C,*D,*E,*F,*G,*H,*I;    
    A = new node('A'); B = new node('B'); C = new node('C'); 
    D = new node('D'); E = new node('E'); F = new node('F'); 
    G = new node('G'); H = new node('H'); I = new node('I');
    E->l = B; E->r = G;      B->l = A; B->r = D;
    G->l = F; G->r = I;      D->l = C;       I->l = H;

    cout <<"in order:   ";    inorder(E); cout << endl;    //打印中序序列
    cout <<"pre order:  ";   preorder(E); cout << endl;    //打印先序序列
    cout <<"post order: ";  postorder(E); cout << endl;    //打印后序序列
    remove_tree(E); 
    return 0;
}

  DFS是一直深入的，适合处理节点间的先后关系、连通性等，在图论中应用很广泛。
  具体内容，请参考《算法竞赛入门到进阶》第10章图论。

4.2 DFS代码框架

  DFS的代码看起来比较简单，但是逻辑上难以理解，不容易编码。
  下面给出DFS的框架。在后续“剪枝”这一篇中的例题“hdu 1010 Tempter of the Bone”，是非常符合这个框架的示例，请仔细分析例题代码。
  读者在大量编码的基础上，再回头体会这个框架的作用。

ans;                  //答案，用全局变量表示
void dfs(层数，其他参数){
    if (出局判断){    //到达最底层，或者满足条件退出 
        更新答案;     //答案一般用全局变量表示
        return;       //返回到上一层
    }
    (剪枝)            //在进一步DFS之前剪枝
    for (枚举下一层可能的情况)    //对每一个情况继续DFS 
        if (used[i] == 0) {       //如果状态i没有用过，就可以进入下一层
            used[i] = 1;   //标记状态i,表示已经用过，在更底层不能再使用
            dfs(层数+1，其他参数);    //下一层 
            used[i] = 0;   //恢复状态，回溯时，不影响上一层对这个状态的使用
            }
    return;          //返回到上一层
}

5 BFS和DFS的复杂度

  以图为例，图中的所有n个点和所有m条边都应该至少访问一次，所以复杂度至少是O(n+m)的。很多情况下，点和边会计算多次。例如计算图上两个点之间的最短路径，一条路径包含很多点和边，一个点或一个边可能属于不同的路径，需要计算多次，复杂度就会超过O(n+m)。
  在BFS和DFS基础上，发展出了剪枝、记忆化（DFS）、双向广搜（BFS）、迭代加深搜索（DFS）、A*（BFS）等技术，大大增强了搜索的能力。
  DFS的代码比BFS更简单，如果一个问题用BFS和DFS都行，一般用DFS。
  搜索的题目，关键往往在于去重。例如BFS的队列，把状态放进队列时，需要判断这个状态是否已经在队列中处理过，如果已经处理过，就不用放进队列，这就是去重。去重能大大优化复杂度。去重用hash很方便，缺点是很浪费空间。

6 BFS和DFS基本题目

  在《算法入门到进阶》第4章中，讲解了一些经典题目：排列问题、子集生成和组合问题、八数码问题、八皇后问题、埃及分数等。
  后续几篇将深入讲解一些例题。
  基本的搜索题练习，请参考：
  力扣的DFS题：https://leetcode-cn.com/tag/depth-first-search/
  力扣的BFS题：https://leetcode-cn.com/tag/breadth-first-search/
  洛谷训练场的BFS和DFS：https://www.luogu.com.cn/training/mainpage
  竞赛队员掌握基本搜索的编码能力，重要性是毋庸置疑的，参赛得奖就有保障了。
  初学者应该大量做搜索题，达到心手合一的境界，“唯手熟尔”!