第七课_进制4_进制的运算
前言
今天要带大家了解一下进制运算的本质。只要了解了这个本质,理论上任何进制你都可以进行加、减、乘、除的运算。学会了这种方法,到后面学了C语言的时候你就可以用这种方法设置进制的加密算法。扯远了,希望本id能写到C语言。
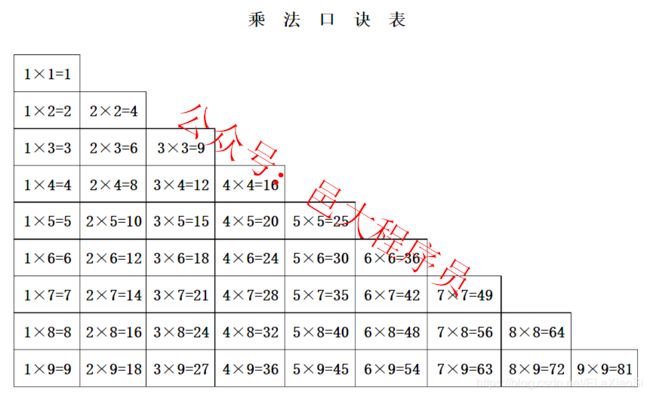
首先问大家一个问题:大家为什么知道1X1=1,2X2=4?
还没想到?先放张图。
看到这张乘法表,我们就应该知道,我们之所以能熟练地进行十进制的运算,全凭我们脑中有两张表,一个是十进制的加法表,另一张是十进制的乘法表。想想我们小学的时候背了多久的乘法口诀,被罚抄了多少次乘法表。虽然我们可以进行任意十进制的运算,但是绝大部分人都不会意识到其实我们只是记住了一个加法表和一个乘法表,其实最主要的是加法表,因为乘法表可以通过加法表得到。
其实任何进制的加、减、乘、除的运算的本质就是查表。
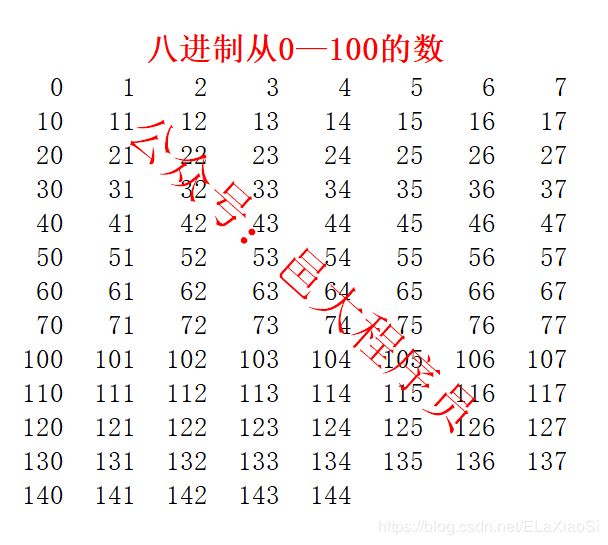
所以最关键的是弄出这两个表来, 而要弄出加法表、乘法表,就必须学会进制的表示。通过上一节课《》的学习,相信是很容易得到8进制从0-100的数,如下图:
下面讲解如何上图中的数制作八进制的加法表和乘法表。
制作加法表
方法:加法表是通过查表查出来的,一个数加上多少,就从这个数开始向后数几个,数到的那个数就是相加得到的结果。
下面举几个例子说明一下:
例1:八进制2 + 4 = ?,过程如下图。
讲解:先从八进制表中找到2,然后往后数4个,得到的数是6,所以八进制的2 + 4 = 6。
例2:八进制的2 + 7 = ?,过程如下图:
讲解:先从八进制中找到2,然后往后数7位,得到11,所以八进制的2 + 7 = 11。
根据这种查表的方法,可以填写出如下的八进制加法表:
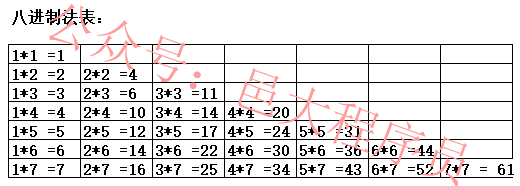
制作乘法表
方法:可以结合加法表和八进制数据表,查出八进制的乘法表。
下面也举两个例子。
例1:2 X 5 = ?
讲解:2 X 5可以看成是5 + 5,根据上面的加法表可以得到5 + 5 = 12,所以2 X 5 = 12。
例2:3 X 6 = ?
讲解:3 X 6可以看成6 + 6 + 6,根据上面的加法表得到6 + 6 = 14,然后再计算14 + 6,这可以查八进制数据表,14往后数6个,得到22,所以最终得到3 X 6 = 22。
使用这种方法就可以得到八进制的乘法表。
进制的加法
任何进制的加法都可以使用查表方式查出来。从右向左一位一位的查。
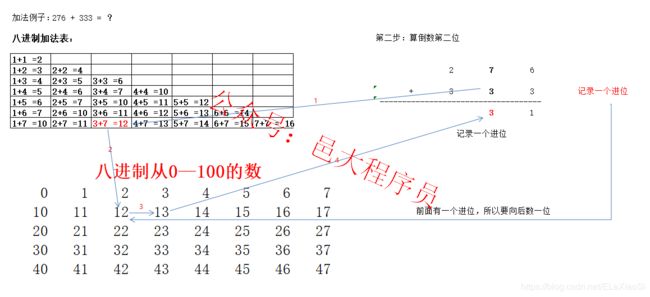
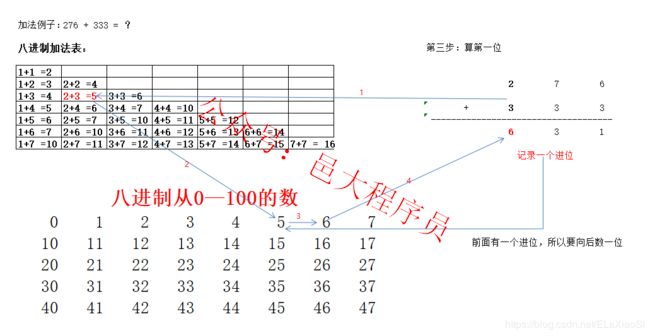
举一个例子:276 + 333 = ?
第一步从最后一位向左算,先算6 + 3,查加法表得到是11,下面写1,并记录一个进位。
然后往前算,7 + 3,查加法表得到是12,因为前面有一个记录的进位,所以要在八进制数表中找到12,然后向后数一个数,得到13,下面写3,并记录一个进位。
再往前算,2 + 3,查加法表得到是5,因为前面也有一个记录的进位,所以要在八进制数表中找到5,然后向后数一个数,得到6,然后下面写6。这样就可以得到最后的结果是631 。
进制的减法
进制的减法和加法的方式是一样的,只是换了思考方式,如a - b ,可以思考成什么加b等于a。
举个例子:71 - 25 = ?
先算1 - 5,我们可以理解成什么加5等于1,或者等于的数最后一位是1的,可以找到4 + 5 = 11,所以1要向前面的7借一位。当然你也可以这样考虑,1 - 5不够减,向前面的7借一位,自己就成了11,然后找什么加5等于11 ,也可以找到4 。
然后算7 - 2,因为之前7被借了1位,所以成了6 - 2,查加法表,什么加2 等于6,找到2 + 4 = 6,所以下面写4,得到最后的结果是44。
进制的乘法
进制的乘法也是通过查表来求得结果的。如果是多位相乘,先分别每位相乘,然后再相加。
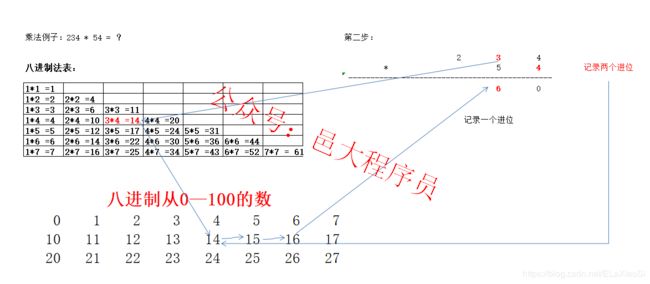
举个例子:234 * 54 = ?
先算4 * 4,在八进制乘法表中查到,4 * 4 = 20 ,下面写0,并记录两个进位。
然后算3 * 4,在八进制乘法表中查到3 * 4 = 14,因为前面有两个进位,所以还有在八进制数据表中找到14,再向后找两个数,得到16,所以下面写6,并记录一个进位。
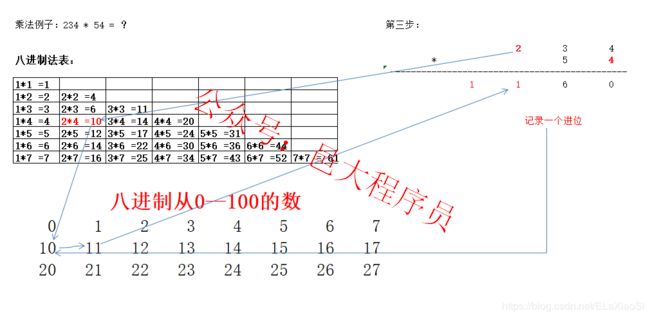
然后再算2 * 4,在八进制乘法表中查到2 * 4 = 10,因为前面有一个进位,所以还要在八进制数据表中找到10,然后向后数一位,得到11,又因为前面没有数,直接就在下面写11 。
类似的方法查出234 * 5 的结果,注意数位的对应。得到如下式子。
然后把得到的两个乘积相加,这就前面讲过的进制的加法的问题了。最后相加得到15320 。
进制的除法
进制的除法也是通过查表求出来的,思维转变一下就是进制的乘法。就不再举例子了。
后言
其他进制的运算跟十进制差不多,只是我们没有意识到我们是通过查表得出的结果,通过前面对八进制的举例说明,发现很多跟十进制有很多相似的地方。所以其他进制也是类似的,也包括自定义的进制数,用进制进行加密,对不懂进制的人来说就是一种极大的障碍。
写于2020.3.1 23 :14