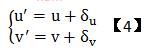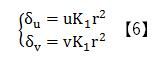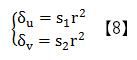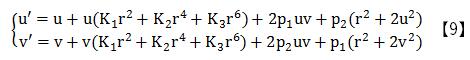摄像机标定技术及其应用——单目摄像机
摄像机标定技术及其应用——单目摄像机
一、为什么要进行摄像机标定
随着机器视觉的迅猛发展,我们已经不满足于使用摄像机进行监控、抓拍这种较为简单的功能。更多的用户青睐于它在非接触三维尺寸测量上的应用。我们所谓的三维测量是广义的三维测量,它不仅包括三维物体的重构与测量,还包括在三维空间中识别任意二维平面上的尺寸以及位置。这种技术目前已被应用在高精度的工业模具以及装配测量中,其中任意二维平面上的尺寸检测技术应用得更为广泛。
图1
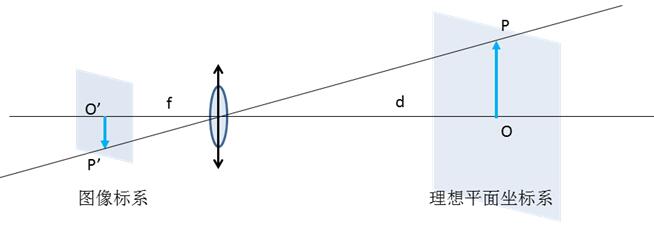
如图1当被测平面和像平面平行且成像模型为理想的小孔成像模型,我们设焦距为f、工作距离为d,则被测物OP和它的像O’P’关系可简单的表示为:
|OP|=|O’P’|×d/f 【1】
但是在实际应用中并非如此,我们无法严格控制像平面和被测平面的位置,所用的镜头也不是严格的小孔模型。如果直接使用【1】式计算将会产生极大的误差。因此,为了获取更高的测量精度,我们需要通过标定来实现坐标平面的转换以及图像的校正。
图2
二、什么是摄像机标定
在实际应用中,被测平面的不确定性以及镜头的畸变使我们已经无法简单的使用【1】式计算出实际距离,但是我们可以将目前能够获得的数据进行转换,使这些数据符合【1】式的使用条件。也就是将任意坐标平面通过旋转和平移映射到理想坐标平面上,对有畸变的图像进行校正,让它成为符合小孔成像模型的像平面。有了这种方法,我们只要确定转换算法、校正算法以及【1】式中的参数就可以实现三维空间中任意平面上尺寸与位置的测量。我们将这种确定参数的过程称之为标定。
三、摄像机单目标定
摄像机标定的方法根据摄像机的数目可分为单目标定、双目标定以及多目标定。其中单目摄像机标定是双目标定的基础,而多目摄像机的标定则是双目摄像机的扩展。因此,我们今天首先来为大家介绍单目标定。在平面测量中影响我们拍摄图像形变的因素有两个:镜头和摄像机的姿态。根据这两个因素我们将摄像机的参数分为两组,摄像机内参和摄像机外参。
1. 摄像机内参
图3
内参一般包括镜头的焦距f、镜头畸变参数k、光轴中心坐标(Cx,Cy)以及像元尺寸Sx,Sy,当摄像机和镜头确定时,这些参数唯一确定。下面我们来详细介绍一下各参数的数学模型。
1) 焦距
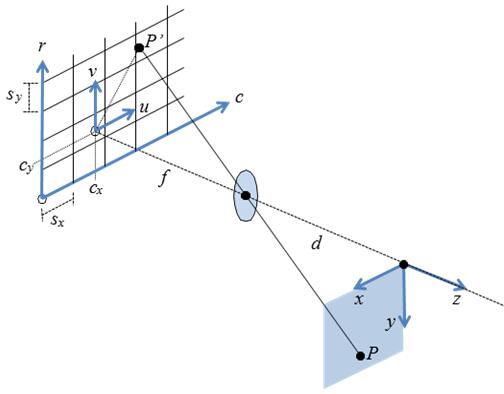
根据镜头类型不同焦距的计算可分为针孔模型和远心模型。如图3我们假设世界坐标系有任一点P(x,y),在摄像机靶面所成的像为P’(u,v),根据不同的光路模型它们之间有如下的对应关系
a) 针孔模型
b) 远心模型
由于远心镜头特殊的光路设计使得像的大小与拍摄距离无关,因此表达式比针孔模型更为简单。
2) 镜头畸变
受到镜头的制作和安装精度的影响,我们所获得图像会产生非线性失真。我们称这种失真为镜头畸变。镜头畸变产生的误差使得理想针孔模型已不再适用。因此我们需要先将所得图像进行校正,再应用理想的针孔模型。假设我们所获取的原始图像坐标(u,v)、校正后的结果(u’,v’),其畸变模型坐标关系为:
a) 径向畸变
图4
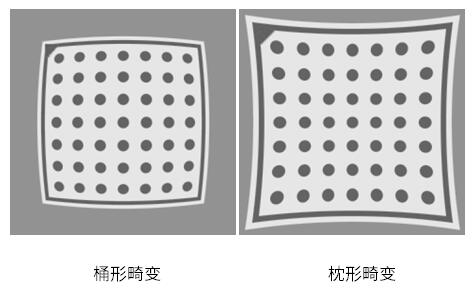
径向畸变主要由透镜制作过程中表面曲率引起,它会使图像发生桶形畸变和枕形畸变(如图4)。其数学模型如下:
其中r2=u2+v2,如果对精度要求不是很高我们可以令K2=0,K3=0将上式简化为如下表达式:
b) 离心畸变
离心变量又称偏心变量,它的误差来源于透镜的安装精度,这主要是因为所有镜片的光学中心并不能严格的保证在同一条直线上。这种误差除了在引入径向畸变同时还会引入切向畸变。由于之前我们已经进行了径向畸变的校正,因此我们在此基础上只需加入切向畸变校正即可。其数学模型如下:
c) 薄棱镜畸变
影响薄棱镜畸变的主要因素的是透镜以及摄像机靶面的平行度,镜片与摄像机靶面夹角越大畸变就越严重。其数学表达式如下:
d) 畸变校正
在实际的应用中,大多数工业摄像机的厂商可以通过摄像机接口螺纹的机械精度来保证镜头透镜与靶面的平行性,而且这种畸变产生的误差较小,因此在一般的图像标定中不作考虑。至此,我们已经基本掌握了大多数情况下畸变产生的原因以及数学模型。结合【5】、【7】两式我们可以推导出镜头畸变校正模型:
2. 摄像机外参
摄像机的外参是指摄像机坐标系与世界坐标系的转换参数它主要由旋转矩阵R和平移矩阵T组成。对于任意三维坐标系,我们都可以通过这两个矩阵将其转换到摄像机坐标系中。其数学模型为c=(x,y,z)T=R∙Pw+T 【10】
1) 旋转矩阵R
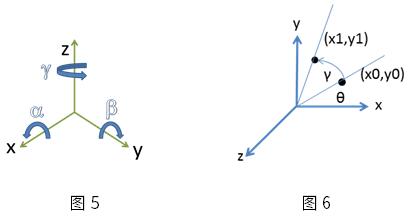
如图5所示,我们通过沿坐标轴x、y、z分别旋转α、β、γ来实现坐标系的转换。因此,旋转矩阵R可分解为Rx(α)、Ry(β)、Rz(γ)三个矩阵相乘的形式。我们以z轴为例,假设(x0,y0)与x轴夹角为θ,且到原点距离为r,通过旋转矩阵
Rz(γ)坐标系沿z轴旋转γ后得到点(x1,y1),我们可得方程组:
x1=r·cos(θ+γ) 【11】
y1=r·sin(θ+γ) 【12】
由三角函数展开得:
x1= r·cos(θ) cos(γ)- r·sin(θ) sin(γ) 【13】
y1= r·sin(θ) cos(γ)+ r·cos(θ) sin(γ) 【14】
由(x0,y0)与x轴夹角为θ得:
x0=r·cos(θ) 【15】
y0=r·sin(θ) 【16】
将【15】式带入【13】式、【16】式带入【14】式得:
x1=x0·cos(γ)-y0·sin(γ) 【17】
y1=y0·cos(γ)+x0·sin(γ) 【18】
以此类推求得Rx(α)和Ry(β)将它们与Rz(γ)相乘得:
2) 平移矩阵T
通过旋转矩阵运算后,世界坐标系的三个坐标轴会与摄像机坐标系对应的坐标轴相平行。此时我们已经离我们的目标又近了一步。如图7所示我们现在只要沿各坐标轴做平移运算即可,由此得:
T=(tx,ty,tz)T 【21】
3) 参数求解
根据【2】、【9】、【20】、【21】这几个数学模型,我们可以得知,若想确定一个摄像机与被测平面的相对位置,则需要确定包括内参、外参在内的14个参数(f,κ1,κ2,κ3,sx,sy,cx,cy,α,β,γ,tx,ty,tz) ,其中f,sx,sy,cx,cy是已知的。因此,我们至少需要9个坐标点,构成9个方程才可以解出剩余的9个未知数。在通常情况下,点的分布以覆盖大部分视场为准,获得的数据点越多,统计的参数就越准确。我们一般采用最小二乘法或者线性规划等统计算法来求解相应参数。下面我们以HALCON为例演示一个标定的全过程。
HALCON是德国MVTEC Software GmbH公司开发的一套完善的机器视觉算法软件包。它除了拥有亚像素精度的算法以及高效的处理性能外,在三维重构方面它也有卓越的表现。它的开发环境中自带摄像机标定工具,可以轻松的完成摄像机的标定工作。同时,您还可以使用HALCON生成可打印的标定板文件。下面我们就来介绍一下摄像机标定的整个流程。
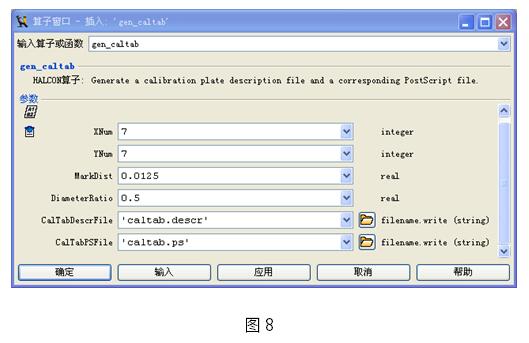
a) 生成标定板
i. 创建标定板
使用HALCON开发环境HDevelop创建标定板
在选择尺寸选择时推荐大家使用边长为视野1/3左右的标定板
ii. 打印标定板
通过GSView等高精度打印软件打印标定板。
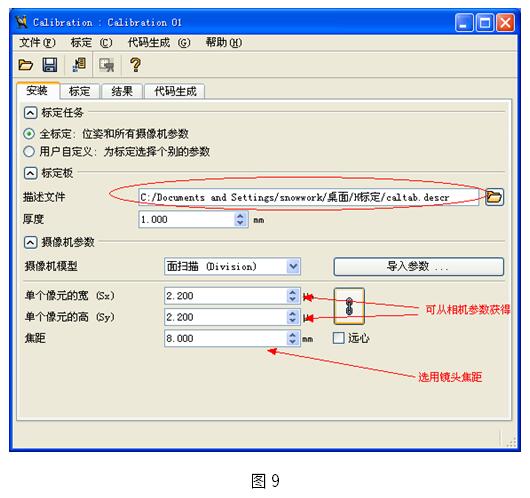
b) 摄像机参数设置
输入所使用的摄像机以及镜头的相关参数
c) 拍摄标定板图像
我们采用平移和倾斜的方式使得拍摄图像中的标定板尽量覆盖整个视场。
一般情况我们需要保存15幅不同位置的图像,具体位置如下:
d) 标定图像载入
通过HALCON我们可以实时拍摄图像也可以读取我们事先拍摄好的图像进行标定。如果标定板识别成功,图像上将绘制出标定板坐标系。
e) 标定
 标定后我们会获得摄像机内参和外参。我们还可以将它们保存起来用于坐标转换或图像校正。
标定后我们会获得摄像机内参和外参。我们还可以将它们保存起来用于坐标转换或图像校正。
f) 验证标定结果
在HALCON中不仅有摄像机标定工具还有测量工具,下面我们使用HDevelop自带的一维测量助手来验证一下我们的标定结果。
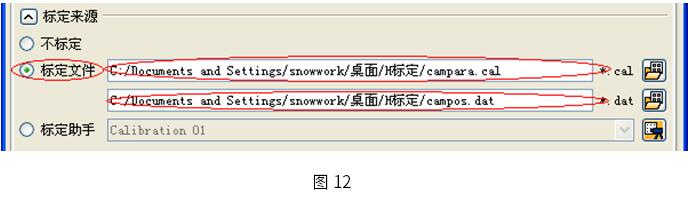
首先我们要加载我们刚才标定的数据。
成功加载标定数据后我们就可以使用我们随机拍摄的一张图像进行测量。
通过以上几步操作,现在我们就已经得到了像素点的实际距离。
图14
复杂的标定工作在HALCON的帮助下就轻松的完成了。不仅如此,以上的所有步骤都可以导出为代码,我们可以将这些代码集成到我们自己的程序中。
备注:若采用高精度的标定板将会得到更高精度的标定结果。
四、应用:
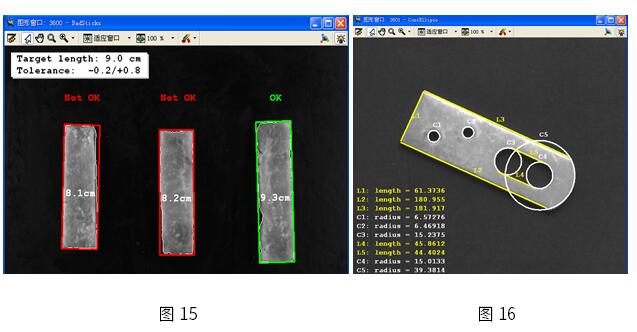
单目摄像机标定技术适用于被测表面曲率较小且需要获取实际数据的应用场合,比如食品、机械制造以及半导体等。理论上,在检测过程中所有的被测物尺寸的判断都可以使用像素尺寸来完成。虽然像素尺寸和实际尺寸对于计算机来说几乎是一样的,一般只用于比较大小,但是对于我们来说实际尺寸更加直观。
图15为速冻鱼柳检测系统的图像处理示例。由于实际应用中不同批次的鱼柳宽度不同,因此,最好的办法是使用标定后获取的实际数据来进行计算。这种判定方法使得系统参数更加直观,设置更加方便。图16为工件尺寸检测系统,通过标定,我们不仅可以获取实际数据,而且可以将它们直接和CAD中数据进行比较,提高检测效率。
五、结语:
在机器视觉产业的蓬勃发展的今天,摄像机标定已经逐步应用到医疗、食品、磨具生产、半导体生产等诸多检测系统中。随着像HALCON这样的算法库用户群的不断扩大,摄像机标定在作为我们研究课题的同时,也会不断的走进工业应用中。它将为我们提供更完善,更精准的二维以及三维空间的解决方案,成为提高工业生产效率和产品质量的推动力。