并查集与带权并查集

并查集算法

概要

并查集作为算法竞赛中较为简单、易用的数据结构，适用于由时序并入的动态集合查找。并查集中的两个主要操作就是“合并集合”与“查找集合”

算法

用集合中的某个元素来代表这个集合，该元素称为集合的代表元。
一个集合内的所有元素组织成以代表元为根的树形结构。
在并查集算法中，合并操作是将该元素所在树连接在被合并元素所在树上。
对于查找操作，即是路经查找到树根，确定代表元的过程。

判断两个元素是否属于同一集合，只需要看他们的代表元是否相同即可。

路径压缩

对于不相交集合的操作，一般采用两种启发式优化的方法：
1. 按秩合并：使包含较少结点的树根指向包含较多结点的树根。
2. 路径压缩：使路径查找上的每个点都直接指向根结点。

在大多数场景中，路径压缩就能满足时间要求。

时间复杂度

对于有 n n 项， m m 次操作的并查集（其中有 f f 次查询），运行时间时间复杂度为：
1. 朴素的并查集： O(n2) O ( n 2 )
2. 带按秩合并的并查集： O(mlgn) O ( m lg ⁡ n )
3. 带路径压缩的并查集： O(n+f⋅(log2+f/nn)) O ( n + f ⋅ ( log 2 + f / n ⁡ n ) )
4. 带路径压缩的按秩合并并查集： O(mα(n)) O ( m α ( n ) )
其中 α(n) α ( n ) 为Ackerman函数反函数，对于实际运用中，可认为 α(n)≤4 α ( n ) ≤ 4

具体实现

void init(int n) { for (int i = 0; i <= n; i++) { f[i] = i; rank[i] = 0;} }

int find(int x) { return x == f[x] ? x : f[x] = find(f[x]); }

void union(int x, iny y){
    x = find(x), y = find(y);
    if(x != y){
        if(rank[x] > rank[y]) f[y] = x;
        else{
            f[x] = y;
            if(rank[x] == rank[y])
                rank[y]++;
        }
    }
}

[POJ 2236] Wireless Network

注意在合并时，我们只需考虑这台电脑与之前已经修复的电脑能否通讯。

#include 
#include 
#include 

using namespace std;
typedef long long ll;
const int N = 1005;

ll f[N], x[N], y[N];
bool vis[N];
int n;
ll d;

bool Con(int u, int v){
    return (x[u] - x[v]) * (x[u] - x[v]) + (y[u] - y[v]) * (y[u] - y[v]) <= d * d;
}
int find(int x){return f[x] == x? x: f[x] = find(f[x]);}
int main()
{
    scanf("%d%lld", &n, &d);
    for(int i = 1; i <= n; i++){
        f[i] = i;
        scanf("%lld%lld",&x[i], &y[i]);
    }
    char ch;
    int u, v;
    while(getchar(), scanf("%c", &ch) != EOF){
        if(ch == 'O'){
            scanf("%d", &u);
            if(!vis[u]){
                for(int i = 1; i <= n; i++){
                    if(!vis[i]) continue;
                    if(Con(i, u)){
                        int fa = find(i), fb = find(u);
                        f[fa] = fb;
                    }
                }
                vis[u] = true;
            }
        }
        else{
            scanf("%d%d", &u, &v);
            int fa = find(u), fb = find(v);
            if(vis[u] && vis[v] && fa == fb) puts("SUCCESS");
            else puts("FAIL");
        }
    }
    return 0;
}

带权并查集

概要

在并查集的基础上，对其中的每一个元素赋有某些值。在对并查集进行路径压缩和合并操作时，这些权值具有一定属性，即可将他们与父节点的关系，变化为与所在树的根结点关系。

统计

[POJ 1988] Cube Stacking

我们需要新增两种属性 cnt[i] c n t [ i ] 与 s[i] s [ i ] ，分别表示 i i 之下的块数和 i i 所在堆的数量。在路径压缩时，cnt[i] += cnt[f[i]] ，另外在连接操作时，需要动态更新cnt[find(u)]和s[find(v)]的信息。

#include 
#include 

const int N = 30005;
int f[N], cnt[N], s[N];

int find(int x){
    if(x != f[x]){
        int fa = f[x];
        f[x] = find(f[x]);
        cnt[x] += cnt[fa];
    }
    return f[x];
}
int main()
{
    for(int i = 0; i < N; i++) {
        f[i] = i;
        s[i] = 1;
    }
    int n;
    scanf("%d", &n);
    char ch;
    int u, v;
    for(int i = 0; i < n; i++){
        getchar();
        scanf("%c", &ch);
        if(ch == 'M'){
            scanf("%d%d", &u, &v);
            int fa = find(u), fb = find(v);
            if(fa != fb){
                f[fa] = fb;
                cnt[fa] = s[fb];
                s[fb] += s[fa];
            }
        }
        else{
            scanf("%d", &u);
            find(u);
            printf("%d\n", cnt[u]);
        }
    }
    return 0;
}

[HDU 3635] Dragon Balls

我们需要新增两种属性 cnt[i] c n t [ i ] 和 trans[i] t r a n s [ i ] ，分别表示该堆数量和转移次数。在路径压缩时，trans[x] += trans[fa]。在合并时，动态更新被合并树的堆数量，并增加合并树的转移次数cnt[fy] += cnt[fx]，trans[fx++]。

#include 
#include 
#include 

const int N = 10005;
int f[N], trans[N], cnt[N];
int n, m, qry, fx, fy, u, v;
char ch[5];

int find(int x){
    if(x != f[x]){
        int fa = f[x];
        f[x] = find(f[x]);
        trans[x] += trans[fa];
    }
    return f[x];
}

void init(int n){
    for(int i = 1; i <= n; i++){
        f[i] = i;
        trans[i] = 0;
        cnt[i] = 1;
    }
}


int main()
{
    int T;
    scanf("%d", &T);
    for(int kase = 1; kase <= T; kase++){
        scanf("%d%d", &n, &qry);
        init(n);
        printf("Case %d:\n", kase);
        for(int i = 0; i < qry; i++){
            scanf("%s", ch);
            if(ch[0] == 'T'){
                scanf("%d%d", &u, &v);
                fx = find(u), fy = find(v);
                if(fx != fy){
                    f[fx] = fy;
                    cnt[fy] += cnt[fx];
                    trans[fx] ++;
                }
            }
            else{
                scanf("%d", &u);
                v = find(u);
                printf("%d %d %d\n", v, cnt[v], trans[u]);
            }
        }
    }
    return 0;
}

区间统计

[HDU 3038] How Many Answers Are Wrong

需要注意：
1. 此类问题需要对所有值统计设置相同的初值，但初值的大小一般没有影响。
2. 对区间[l, r]进行记录时，实际上是对 (l-1, r]操作，即l = l - 1。（即势差是在l-1和r之间）
3. 在进行路径压缩时，可和统计类问题相似的cnt[x] += cnt[fa]（因为势差是直接累计到根结点的）
4. 在合并操作中，对我们需要更新cnt[fb]（由于fb连接到了fa上），动态更新的公式是cnt[fb] = cnt[u - 1] - cnt[v] + d，为了理解这个式子，我们进行如下讨论：
- 更新cnt[fb]的目的是维护被合并的树(fb)相对于合并树(fa)之间的势差。
- cnt[fb] - cnt[fa]两者之间的关系，并不能直接建立，而是通过cnt[u - 1] - cnt[v]之间的关系建立。
- 可知 cnt[v]保存结点v与结点fb之间的势差； cnt[u-1]保存结点u-1与结点fa之间的势差；d是更新信息中结点u-1与结点v之间的势差
- 所以cnt[fb]的值为从结点fb与结点v(-cnt[v])，加上从结点v到结点u(d)，最后加上从结点u-1到结点fa(cnt[u - 1])

#include 
#include 
#include 
#include 
#include 
using namespace std;

typedef long long ll;
const int N = 200005;

int f[N];
ll cnt[N];

int find(int x)
{
    if(x != f[x]){
        int fa = f[x];
        f[x] = find(f[x]);
        cnt[x] += cnt[fa]; 
    }
    return f[x];
}

void init(int n)
{
    for(int i = 0; i <= n; i++){
        f[i] = i;
        cnt[i] = 0;
    }
}

int main()
{
    int n, m;
    while(scanf("%d%d", &n, &m) != EOF){
        int ans = 0;
        init(n);
        int u, v, d, fa, fb;
        for(int i = 0; i < m; i++){
            scanf("%d%d%d", &u, &v, &d);
            fa = find(u - 1), fb = find(v);
            if(fa == fb){
                if(cnt[u - 1] + d != cnt[v])    ans++;
            }
            else{
                f[fb] = fa;
                cnt[fb] = cnt[u - 1] - cnt[v]  + d;
            }
        }
        printf("%d\n", ans);
    }
    return 0;
}

[POJ 1733] Parity game

与上一题类似，由于数据范围较大，需要首先进行离散化。由于只有奇偶两种状态，所以只需要用0和1表示状态即可。在路径压缩时num[x] = num[x] ^ num[fa]（模2系）

#include 
#include 
#include 
#include 
#include 
using namespace std;

typedef long long ll;

const int N = 200005;
const int LEN = 7;

int f[N], num[N], des[2 * N];

struct Query{
    int u, v, d;
}q[N];

int find(int x)
{
    if(x != f[x]){
        int fa = f[x];
        f[x] = find(f[x]);
        num[x] = num[x] ^ num[fa]; 
    }
    return f[x];
}

void init(int n)
{
    for(int i = 0; i <= n; i++){
        f[i] = i;
        num[i] = 0;
    }
}


int main()
{
    int n, m;
    while(scanf("%d%d", &n, &m) != EOF){
        bool conf = false;
        int ans = 0, cnt = 0;
        int u, v, fa, fb;
        char s[LEN];
        for(int i = 0; i < m; i++){
            scanf("%d%d%s", &q[i].u, &q[i].v, s);
            if(s[0] == 'o') q[i].d = 1;
            else q[i].d = 0;
            des[cnt++] = q[i].u - 1;
            des[cnt++] = q[i].v;
        }
        sort(des, des + cnt);
        cnt = unique(des, des + cnt) - des;
        init(cnt);
        for(int i = 0; i < m; i++){
            if(!conf){
                u = lower_bound(des, des + cnt, q[i].u - 1) - des;
                v = lower_bound(des, des + cnt, q[i].v) - des;
                fa = find(u), fb = find(v);
                if(fa == fb){
                    if((num[u] + q[i].d) % 2 != num[v]) conf = true;
                }
                else{
                    f[fb] = fa;
                    num[fb] = (2 + num[u] - num[v] + q[i].d) % 2;
                }
                if(!conf) ans++;
            }
        }
        printf("%d\n", ans);
    }
    return 0;
}

种类并查集

[HDU 3047] Zjnu Stadium

注意到座位编号是1~300，所以是一个模300系。相对于区间统计类的并查集，这里的pos[i]可以被理解为每个人的种类。其他操作类似于区间统计类的并查集。

#include 
#include 
#include 

using namespace std;

const int N = 50005;
const int MOD = 300;

int f[N], pos[N];

int find(int x){
    if(x != f[x]){
        int fa = f[x];
        f[x] = find(f[x]);
        pos[x] = (pos[x] + pos[fa]) % MOD;
    }
    return f[x];
}

void init(int n){
    for(int i = 0; i <= n; i++){    
        f[i] = i;
        pos[i] = 0;     
    }
}

int main()
{
    int n, m, ans;
    while(scanf("%d%d", &n, &m) != EOF){
        init(n);
        int u, v, d, fa, fb;
        ans = 0;
        for(int i = 0; i < m; i++){
            scanf("%d%d%d", &u, &v, &d);
            fa = find(u), fb = find(v);
            if(fa == fb){
                if(pos[v] != (pos[u] + d) % MOD){
                    ans++;
                }
            }
            else{
                f[fb] = fa;
                pos[fb] = (MOD - pos[v] + pos[u] + d) % MOD;    
            }
        }
        printf("%d\n", ans);
    }
    return 0;
}

[POJ 1182] 食物链

可参考:http://blog.csdn.net/c0de4fun/article/details/7318642
对于这三种种类，同类可以用0表示，其他两种分别用1表示该结点被父节点吃，2表示该节点吃父节点。
该题之所以能用并查集进行路径压缩，是因为存在A吃B，B吃C，C吃A的三角关系。这是我们能在路径压缩中使用num[x] = (num[x] + num[fa]) % 3和更新时使用num[fb] = (3 - num[v] + num[u] + (p - 1)) % 3的原因（否则就是一种链式关系了）。

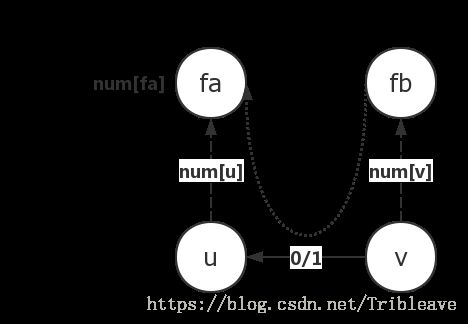
关于num[fb] = (3 - num[v] + num[u] + (p - 1)) % 3的推导，我们可以画图来理解。
我们能够获得的信息是num[fa] num[u] num[v]与u v之间的关系，有一个很好的性质就是在该模3系中，关系是可以逆推的，即如果把从v到fb的链反向，那么fb相对于v的关系就是3-num[v]
如图所示，我们在这些关系的基础上，要获得fb相对于fa的关系，直接将“关系”进行（反转）相加即可。

#include 
#include 
#include 
#include 

using namespace std;

const int N = 50005;

int f[N], num[N];

int find(int x){
    if(x != f[x]){
        int fa = f[x];
        f[x] = find(f[x]);
        num[x] = (num[x] + num[fa]) % 3;
    }
    return f[x];
}

int main()
{
    int n, q, ans = 0;
    scanf("%d%d", &n, &q);
    for(int i = 0; i < n; i++)  f[i] = i;
    for(int i = 0; i < q; i++){
        int p, u, v;
        scanf("%d%d%d", &p, &u, &v);
        if(u > n || v > n)  ans++;
        else if(p == 2 && u == v)   ans++;
        else{
            int fa = find(u), fb = find(v);
            if(fa == fb){
                if(num[v] != (num[u] + (p - 1)) % 3)
                    ans++;
            }
            else{
                f[fb] = fa;
                num[fb] = (3 - num[v] + num[u] + (p - 1)) % 3;
            }
        }
    }
    printf("%d\n", ans);
    return 0;
}

[POJ 2912] Rochambeau

基础操作与食物链非常相似，但是有可能出现一个或多个异常。在以下方法中，我们枚举每个人是异常的情况，观察有多少个人可能是裁判。如果有多个人成为裁判使体系融洽，那么不能确定；如果没有一个人成为裁判后体系融洽，那么就没有答案；如果只有一个人可能成为裁判，那么我们得出判断的轮数，就是其他人成为裁判时，使体系不融洽的最大轮数。

#include 
#include 
#include 
#include 
using namespace std;

const int N = 505;
const int M = 2005;

struct Res{
    int u, v;
    int r;
}r[M];

int f[N], num[N], err[N];
int n, m;

int find(int x){
    if(x != f[x]){
        int fa = f[x];
        f[x] = find(f[x]);
        num[x] = (num[x] + num[fa]) % 3;
    }
    return f[x];
}
void init(int n){
    for(int i = 0; i < n; i++) {
        f[i] = i; 
        num[i] = 0;
    }
}

int main(){
    while(scanf("%d%d", &n, &m) != EOF){
        for(int i = 0; i < m; i++){
            char ch;
            scanf("%d%c%d", &r[i].u, &ch, &r[i].v);
            if(ch == '=')   r[i].r = 0;
            else if(ch == '<') r[i].r = 1;
            else if(ch == '>') r[i].r = 2;
        }
        memset(err, -1, sizeof(err));
        for(int i = 0; i < n; i++){
            init(n);
            for(int j = 0; j < m; j++){
                if(i == r[j].u || i == r[j].v) continue;
                int fa = find(r[j].u), fb = find(r[j].v);
                if(fa == fb){
                    if(num[r[j].v] != (num[r[j].u] + r[j].r) % 3){
                        err[i] = j + 1;
                        break;
                    }
                }
                else{
                    f[fb] = fa;
                    num[fb] = (num[r[j].u] - num[r[j].v] + 3 + r[j].r) % 3;
                }
            }
        }
        int cnt = 0, ans1 = 0, ans2 = 0;
        for(int i = 0; i < n; i++){
            if(err[i] == -1){
                cnt ++;
                ans1 = i;
            }
            ans2 = max(ans2, err[i]);
        }
        if(cnt == 0)    printf("Impossible\n");
        else if(cnt > 1)    printf("Can not determine\n");
        else printf("Player %d can be determined to be the judge after %d lines\n", ans1, ans2); 
    }
    return 0;
}

[POJ 1703] Find them, Catch them

模2系，只需注意最后三种情况的判断。

#include 
#include 
#include 
#include 

using namespace std;

const int N = 100005;

int f[N], num[N];

int find(int x){
    if(x != f[x]){
        int fa = f[x];
        f[x] = find(f[x]);
        num[x] = (num[x] + num[fa]) % 2; 
    }
    return f[x];
}

void init(int n){
    for(int i = 0; i <= n; i++){
        f[i] = i;

        num[i] = 0;
    }
}

int main()
{
    int T, n, q;
    scanf("%d", &T);
    for(int i = 0; i < T; i++){
        scanf("%d%d", &n, &q);
        init(n);
        for(int i = 0; i < q; i++){
            char ch;
            int u, v;
            getchar();
            scanf("%c%d%d", &ch, &u, &v);
            int fa = find(u), fb = find(v);
            if(ch == 'D'){
                f[fb] = fa;
                num[fb] = (1 - num[v] + num[u]) % 2;
            }
            else{
                if(fa != fb)    printf("Not sure yet.\n");
                else if(num[u] != num[v])   printf("In different gangs.\n");
                else printf("In the same gang.\n");
            }
        }
    }
    return 0;
}

[POJ 2492] A Bug’s Life

#include 
#include 
#include 
#include 

using namespace std;

const int N = 2005;

int f[N], num[N];
int n, m, u, v;

int find(int x)
{
    if(x != f[x]){
        int fa = f[x];
        f[x] = find(f[x]);
        num[x] = (num[x] + num[fa]) % 2;
    }
    return f[x];
}

void init(int n)
{
    for(int i = 0 ; i <= n; i++){
        f[i] = i;
        num[i] = 0;
    }
}

int main(){
    int T;
    scanf("%d", &T);
    for(int kase = 1; kase <= T; kase++){
        bool conf = false;
        scanf("%d%d", &n, &m);
        init(n);
        for(int i = 0; i < m; i++){
            scanf("%d%d", &u, &v);
            if(!conf){
                int fa = find(u), fb = find(v);
                if(fa == fb){
                    if(num[u] == num[v])    conf = true;
                }
                else{
                    f[fb] = fa;
                    num[fb] = 1 - num[v] + num[u];
                }
            }
        }
        if(kase > 1) puts("");
        printf("Scenario #%d:\n", kase);
        if(conf) puts("Suspicious bugs found!");
        else puts("No suspicious bugs found!");
    }
    return 0;
}

其他与并查集相关的问题

逆向并查集

[HDU 4496] D-City

由于题目的特殊性，我们可以逆向构建并查集。初始化cnt = n如果发现两者不属于同一集合，有cnt–。对于每一步，有ans[i - 1] = cnt

#include 
#include 
#include 
#include 

using namespace std;

const int N = 10005;
const int M = 100005;

int f[N];
int a[M], b[M], ans[M];

int find(int x){return f[x] == x? x: f[x] = find(f[x]);}

int main()
{
    int n, m;
    while(scanf("%d%d", &n, &m) != EOF){
        for(int i = 0; i <= n; i++)
            f[i] = i;
        for(int i = 1; i <= m; i++)
            scanf("%d%d", &a[i], &b[i]);
        int cnt = n, fa, fb;
        ans[m] = n;
        for(int i = m; i >= 1; i--){
            fa = find(a[i]), fb = find(b[i]);
            if(fa != fb){
                cnt--;
                f[fb] = fa;
            }
            ans[i - 1] = cnt;
        }
        for(int i = 1; i <= m; i++)
            printf("%d\n", ans[i]);
    }
    return 0;
}

可持久化并查集

[BZOJ 3673] 可持久化并查集 by zky

[BZOJ 3674] 可持久化并查集加强版

http://blog.csdn.net/lemonoil/article/details/57085830
http://blog.csdn.net/lemonoil/article/details/57085381
http://blog.csdn.net/lemonoil/article/details/57416510
http://blog.csdn.net/kscla/article/details/53586880
http://blog.csdn.net/iamzky/article/details/38349183
(待填坑)

其他杂题

[UVA 11987] Almost Union-Find

[UVALive 4487] Exclusive-OR

[CodeForces 813F] Bipartite Checking

(待填坑)