k-近邻算法(一)
一 简单k-近邻算法
1 k-近邻法简介
2 距离度量
3 Python3代码实现
31 准备数据集
32 k-近邻算法
33 整体代码
二 k-近邻算法实战之约会网站配对效果判定
1 实战背景
2 准备数据数据解析
3 分析数据数据可视化
4 准备数据数据归一化
5 测试算法验证分类器
6 使用算法构建完整可用系统
三 k-近邻算法实战之sklearn手写数字识别
1 实战背景
2 Sklearn简介
3 Sklearn安装
4 Sklearn实现k-近邻算法简介
5 Sklearn小试牛刀
四 总结
1 kNN算法的优缺点
2 其他
一 简单k-近邻算法
本文将从k-邻近算法的思想开始讲起,使用python3一步一步编写代码进行实战训练。并且,我也提供了相应的数据集,对代码进行了详细的注释。除此之外,本文也对sklearn实现k-邻近算法的方法进行了讲解。实战实例:电影类别分类、约会网站配对效果判定、手写数字识别。
1.1 k-近邻法简介
k近邻法(k-nearest neighbor, k-NN)是1967年由Cover T和Hart P提出的一种基本分类与回归方法。它的工作原理是:存在一个样本数据集合,也称作为训练样本集,并且样本集中每个数据都存在标签,即我们知道样本集中每一个数据与所属分类的对应关系。输入没有标签的新数据后,将新的数据的每个特征与样本集中数据对应的特征进行比较,然后算法提取样本最相似数据(最近邻)的分类标签。一般来说,我们只选择样本数据集中前k个最相似的数据,这就是k-近邻算法中k的出处,通常k是不大于20的整数。最后,选择k个最相似数据中出现次数最多的分类,作为新数据的分类。
举个简单的例子,我们可以使用k-近邻算法分类一个电影是爱情片还是动作片。
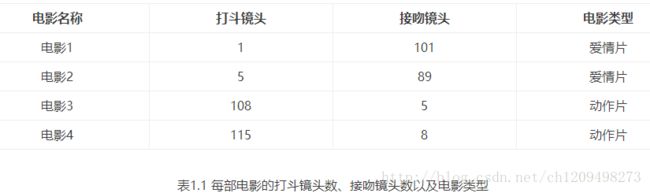
表1.1就是我们已有的数据集合,也就是训练样本集。这个数据集有两个特征,即打斗镜头数和接吻镜头数。除此之外,我们也知道每个电影的所属类型,即分类标签。用肉眼粗略地观察,接吻镜头多的,是爱情片。打斗镜头多的,是动作片。以我们多年的看片经验,这个分类还算合理。如果现在给我一部电影,你告诉我这个电影打斗镜头数和接吻镜头数。不告诉我这个电影类型,我可以根据你给我的信息进行判断,这个电影是属于爱情片还是动作片。而k-近邻算法也可以像我们人一样做到这一点,不同的地方在于,我们的经验更”牛逼”,而k-邻近算法是靠已有的数据。比如,你告诉我这个电影打斗镜头数为2,接吻镜头数为102,我的经验会告诉你这个是爱情片,k-近邻算法也会告诉你这个是爱情片。你又告诉我另一个电影打斗镜头数为49,接吻镜头数为51,我”邪恶”的经验可能会告诉你,这有可能是个”爱情动作片”,画面太美,我不敢想象。 (如果说,你不知道”爱情动作片”是什么?请评论留言与我联系,我需要你这样像我一样纯洁的朋友。) 但是k-近邻算法不会告诉你这些,因为在它的眼里,电影类型只有爱情片和动作片,它会提取样本集中特征最相似数据(最邻近)的分类标签,得到的结果可能是爱情片,也可能是动作片,但绝不会是”爱情动作片”。当然,这些取决于数据集的大小以及最近邻的判断标准等因素。
1.2 距离度量
我们已经知道k-近邻算法根据特征比较,然后提取样本集中特征最相似数据(最邻近)的分类标签。那么,如何进行比较呢?比如,我们还是以表1.1为例,怎么判断红色圆点标记的电影所属的类别呢?如图1.1所示。
![]()
我们可以从散点图大致推断,这个红色圆点标记的电影可能属于动作片,因为距离已知的那两个动作片的圆点更近。k-近邻算法用什么方法进行判断呢?没错,就是距离度量。这个电影分类的例子有2个特征,也就是在2维实数向量空间,可以使用我们高中学过的两点距离公式计算距离,如图1.2所示。
![]()
图1.2 两点距离公式
通过计算,我们可以得到如下结果:
(101,20)->动作片(108,5)的距离约为16.55
(101,20)->动作片(115,8)的距离约为18.44
(101,20)->爱情片(5,89)的距离约为118.22
(101,20)->爱情片(1,101)的距离约为128.69
通过计算可知,红色圆点标记的电影到动作片 (108,5)的距离最近,为16.55。如果算法直接根据这个结果,判断该红色圆点标记的电影为动作片,这个算法就是最近邻算法,而非k-近邻算法。那么k-邻近算法是什么呢?k-近邻算法步骤如下:
计算已知类别数据集中的点与当前点之间的距离;
按照距离递增次序排序;
选取与当前点距离最小的k个点;
确定前k个点所在类别的出现频率;
返回前k个点所出现频率最高的类别作为当前点的预测分类。
比如,现在我这个k值取3,那么在电影例子中,按距离依次排序的三个点分别是动作片(108,5)、动作片(115,8)、爱情片(5,89)。在这三个点中,动作片出现的频率为三分之二,爱情片出现的频率为三分之一,所以该红色圆点标记的电影为动作片。这个判别过程就是k-近邻算法。
1.3 Python3代码实现
我们已经知道了k-近邻算法的原理,那么接下来就是使用Python3实现该算法,依然以电影分类为例。
1.3.1 准备数据集
对于表1.1中的数据,我们可以使用numpy直接创建,代码如下:
# -*- coding: UTF-8 -*-
import numpy as np
"""
函数说明:创建数据集
"""
def createDataSet():
#四组二维特征
group = np.array([[1,101],[5,89],[108,5],[115,8]])
#四组特征的标签
labels = ['爱情片','爱情片','动作片','动作片']
return group, labels
if __name__ == '__main__':
#创建数据集
group, labels = createDataSet()
#打印数据集
print(group)
print(labels)[[ 1 101]
[ 5 89]
[108 5]
[115 8]]
['爱情片', '爱情片', '动作片', '动作片']1.3.2 k-近邻算法
根据两点距离公式,计算距离,选择距离最小的前k个点,并返回分类结果。
# -*- coding: UTF-8 -*-
import numpy as np
import operator
"""
函数说明:kNN算法,分类器
Parameters:
inX - 用于分类的数据(测试集)
dataSet - 用于训练的数据(训练集)
labes - 分类标签
k - kNN算法参数,选择距离最小的k个点
Returns:
sortedClassCount[0][0] - 分类结果
"""
def classify0(inX, dataSet, labels, k):
#numpy函数shape[0]返回dataSet的行数
dataSetSize = dataSet.shape[0]
#在列向量方向上重复inX共1次(横向),行向量方向上重复inX共dataSetSize次(纵向)
diffMat = np.tile(inX, (dataSetSize, 1)) - dataSet
#二维特征相减后平方
sqDiffMat = diffMat**2
#sum()所有元素相加,sum(0)列相加,sum(1)行相加
sqDistances = sqDiffMat.sum(axis=1)
#开方,计算出距离
distances = sqDistances**0.5
#返回distances中元素从小到大排序后的索引值
sortedDistIndices = distances.argsort()
#定一个记录类别次数的字典
classCount = {}
for i in range(k):
#取出前k个元素的类别
voteIlabel = labels[sortedDistIndices[i]]
#dict.get(key,default=None),字典的get()方法,返回指定键的值,如果值不在字典中返回默认值。
#计算类别次数
classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1
#python3中用items()替换python2中的iteritems()
#key=operator.itemgetter(1)根据字典的值进行排序
#key=operator.itemgetter(0)根据字典的键进行排序
#reverse降序排序字典
sortedClassCount = sorted(classCount.items(),key=operator.itemgetter(1),reverse=True)
#返回次数最多的类别,即所要分类的类别
return sortedClassCount[0][0]1.3.3 整体代码
这里预测红色圆点标记的电影(101,20)的类别,K-NN的k值为3。创建kNN_test01.py文件,编写代码如下:
# -*- coding: UTF-8 -*-
import numpy as np
import operator
"""
函数说明:创建数据集
Parameters:
无
Returns:
group - 数据集
labels - 分类标签
"""
def createDataSet():
#四组二维特征
group = np.array([[1,101],[5,89],[108,5],[115,8]])
#四组特征的标签
labels = ['爱情片','爱情片','动作片','动作片']
return group, labels
"""
函数说明:kNN算法,分类器
Parameters:
inX - 用于分类的数据(测试集)
dataSet - 用于训练的数据(训练集)
labes - 分类标签
k - kNN算法参数,选择距离最小的k个点
Returns:
sortedClassCount[0][0] - 分类结果
"""
def classify0(inX, dataSet, labels, k):
#numpy函数shape[0]返回dataSet的行数
dataSetSize = dataSet.shape[0]
#在列向量方向上重复inX共1次(横向),行向量方向上重复inX共dataSetSize次(纵向)
diffMat = np.tile(inX, (dataSetSize, 1)) - dataSet
#二维特征相减后平方
sqDiffMat = diffMat**2
#sum()所有元素相加,sum(0)列相加,sum(1)行相加
sqDistances = sqDiffMat.sum(axis=1)
#开方,计算出距离
distances = sqDistances**0.5
#返回distances中元素从小到大排序后的索引值
sortedDistIndices = distances.argsort()
#定一个记录类别次数的字典
classCount = {}
for i in range(k):
#取出前k个元素的类别
voteIlabel = labels[sortedDistIndices[i]]
#dict.get(key,default=None),字典的get()方法,返回指定键的值,如果值不在字典中返回默认值。
#计算类别次数
classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1
#python3中用items()替换python2中的iteritems()
#key=operator.itemgetter(1)根据字典的值进行排序
#key=operator.itemgetter(0)根据字典的键进行排序
#reverse降序排序字典
sortedClassCount = sorted(classCount.items(),key=operator.itemgetter(1),reverse=True)
#返回次数最多的类别,即所要分类的类别
return sortedClassCount[0][0]
if __name__ == '__main__':
#创建数据集
group, labels = createDataSet()
#测试集
test = [101,20]
#kNN分类
test_class = classify0(test, group, labels, 3)
#打印分类结果
print(test_class)动作片可以看到,分类结果根据我们的”经验”,是正确的,尽管这种分类比较耗时,用时1.4s。
到这里,也许有人早已经发现,电影例子中的特征是2维的,这样的距离度量可以用两 点距离公式计算,但是如果是更高维的呢?对,没错。我们可以用欧氏距离(也称欧几里德度量),如图1.5所示。我们高中所学的两点距离公式就是欧氏距离在二维空间上的公式,也就是欧氏距离的n的值为2的情况。
![]()
图1.5 欧氏距离公式
看到这里,有人可能会问:“分类器何种情况下会出错?”或者“答案是否总是正确的?”答案是否定的,分类器并不会得到百分百正确的结果,我们可以使用多种方法检测分类器的正确率。此外分类器的性能也会受到多种因素的影响,如分类器设置和数据集等。不同的算法在不同数据集上的表现可能完全不同。为了测试分类器的效果,我们可以使用已知答案的数据,当然答案不能告诉分类器,检验分类器给出的结果是否符合预期结果。通过大量的测试数据,我们可以得到分类器的错误率-分类器给出错误结果的次数除以测试执行的总数。错误率是常用的评估方法,主要用于评估分类器在某个数据集上的执行效果。完美分类器的错误率为0,最差分类器的错误率是1.0。同时,我们也不难发现,k-近邻算法没有进行数据的训练,直接使用未知的数据与已知的数据进行比较,得到结果。因此,可以说k-邻近算法不具有显式的学习过程。