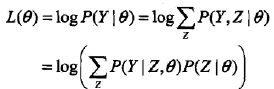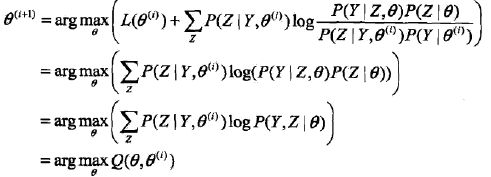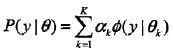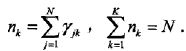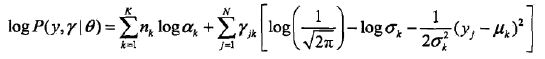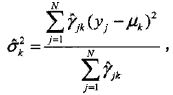统计学习方法 李航---第9章 EM算法及其推广

第9章 EM算法及其推广

EM算法是一种迭代算法，用于含有隐 变量(hidden variable)的概率模型参数的极大似然估计，或极大后验概率估计。 EM算法的每次迭代由两步组成：E步，求期望(expectation)；M步，求极大 ( maximization )，所以这一算法称为期望极大算法(expectation maximization  algorithm)，简称EM算法 。

9.1  EM算法的引入

 

一般地，用Y表示观测随机变量的数据，Z表示隐随机变量的数据。Y和Z 连在一起称为完全数据( complete-data )，观测数据Y又称为不完全数据 (incomplete-data)。假设给定观测数据Y，其概率分布是P(Y | theta)，其中 theta 是需要 估计的模型参数，那么不完全数据Y的似然函数是 P(Y | theta) ，对数似然函数 L(theta)=log P(Y | theta)； 假设Y和Z的联合概率分布是P(Y, Z }句，那么完全数据的对 数似然函数是log P(Y, Z  | theta )。

观测数据的似然函数为

EM算法通过迭代求 L(theta)=log P(Y | theta) 的极大似然估计。每次迭代包含两步 E步，求期望；M步，求极大化。

定义9.1 ( Q函数) 完全数据的对数似然函数 log P(Y, Z  | theta ) 关于在给定观测 数据Y和当前参数 theta⁽ⁱ⁾ 下对未观测数据Z的条件概率分布P(Z | Y, theta ⁽ⁱ⁾ )的期望称 为Q函数，即

EM算法说明:

    步骤(1)参数的初值可以任意选择。但需注意EM算法对初值是敏感的。

    步骤(2)  E步求Q( theta ,  theta ⁽ⁱ⁾ )。Q函数式中Z是未观测数据，Y是观测数据。注 意， Q( theta ,  theta ⁽ⁱ⁾ ) 的第1个变量 theta 表示要极大化的参数，第2个变量 theta ⁽ⁱ⁾ 表示参数的当前估 计值。每次迭代实际在求Q函数及其极大。

    步 骤 (3)  M步求 Q( theta ,  theta ⁽ⁱ⁾ ) 的极大化，得到 theta ⁽ⁱ⁺¹⁾ ，完成一次迭代 theta ⁽ⁱ⁾ -->theta ⁽ⁱ⁺¹⁾。 后面将证明每次迭代使似然函数增大或达到局部极值。

    步骤(4)给出停止迭代的条件，一般是对较小的正数，若满足

则停止迭代.

EM算法的导出

 

通过近似求解观测数据的对数似然函数的极大化问题来导出EM算 法，由此可以清楚地看出EM算法的作用。 面对一个含有隐变量的概率模型，目标是极大化观测数据(不完全数据) Y关于参数 theta

的对数似然函数，即极大化

这一极大化的主要困难是式中有未观测数据并有包含和(或积分) 的对数。

EM算法是通过迭代逐步近似极大化 L(theta) 的。

每次迭代需要满足：新估计值   theta能使 L(theta)增加， 并逐步 达到极大值。i次迭代前后的差值为：

利用jensen不等式可以得出下界

   

为使 L(theta)极大，选择 theta ^{(i+1)使B极大，可得，}

等价于EM算法的一次迭代，即求Q函数及其极大化。EM算法是通过 不断求解下界的极大化逼近求解对数似然函数极大化的算法。

EM算法的直观解释： 图中上方曲线为 L(theta) ，下方曲线为 B ( theta ,  theta ⁽ⁱ⁾ )， 为对数似然函数 L(theta) 的下界，且在   theta= theta ⁽ⁱ⁾ 处相等。 EM算法找到下一个点 theta ⁽ⁱ⁺¹⁾ 使 函数 B ( theta ,  theta ⁽ⁱ⁾ ) 极大化，也使函数Q ( theta ,  theta ⁽ⁱ⁾ ) 极大化。函 数B的增加，保证对数似然函数L在每次迭代中也是增加的。EM算法 在点 theta ⁽ⁱ⁺¹⁾ 重新计算Q函数值，进行下一次迭代。在这个过程中，对数似然函数 L不断增大。从图可以推断出EM算法不能保证找到全局最优值。

EM算法在非监督学习中的应用

训练数据只有输入没有对应的输出(X,？)，从这样的数 据学习模型称为非监督学习问题。EM算法可以用于生成模型的非监督学习，生 成模型由联合概率分布P(X, Y)表示，可以认为非监督学习训练数据是联合概率 分布产生的数据。X为观测数据，Y为未观测数据。

9.2  EM算法的收敛性

定理9.1 设 P(Y | theta) 为观测数据的似然函数， theta ⁽ⁱ⁾  (i=1, 2,... )为EM算法得到 的参数估计序列， P(Y |  theta ⁽ⁱ⁾   ) (i=1, 2,... ) ) 为对应的似然函数序列， 则 P(Y |  theta ⁽ⁱ⁾   ) 是单 调递增的，即

定理9.2 

 

设 P(Y | theta) 为观测数据的似然函数， theta ⁽ⁱ⁾  (i=1, 2,... )为EM算法得到 的参数估计序列， L( theta ⁽ⁱ⁾)= P(Y |  theta ⁽ⁱ⁾   ) (i=1, 2,... ) ) 为对应的似然函数序列，

    (1)如果 P(Y | theta) 有上界，则 L( theta ⁽ⁱ⁾ ) 收敛到某一值L^*;

    (2)在函数Q与L满足一定条件下，由EM算法得到的参数估计序 列 theta ⁽ⁱ⁾ 的收敛值 theta* 是L( theta )的稳定点。

 

 

 

EM算 法的收敛性包含关于对数似然函数序列L的收敛性和关于参数估计序列 theta 的收敛性两层意思，前者并不蕴涵后者。此外，定理只能保证参数估计序列收敛 到对数似然函数序列的稳定点，不能保证收敛到极大值点。所以在应用中，初值 的选择变得非常重要，常用的办法是选取几个不同的初值进行迭代，然后对得到 的各个估计值加以比较，从中选择最好的。

9.3  EM算法在高斯混合模型学习中的应用

定义9.2 (高斯混合模型) 高斯混合模型是指具有如下形式的概率分布模型:

称为第k个分模型。

高斯混合模型参数估计的EM算法

假设观测数据由高斯混合模型生成，

   

1. 明确隐变量。写出完全数据的对数似然函数

可以设想观测数据y _j是这样产生的：首先依概率a _k选择第 k个高斯分布分模型；然后依第k个分模型的概率分布生成观侧

数据 y _j 。 这 时观测数据 y _j 是已知的；反映观测数据 y _j 来自第k 个分模型的数据是未知的，k=1,2,... ,K，为隐变量定义如下：

是0-1随机变量。

那么完全数据是

完全数据的似然函数 为：

  

对数 似 然函数为：

2.  EM算法的E步:确定Q函数

其中。

是在当前模型参数下第j个观测数据来自第k个分模型的概率，称为分模型k 对观测数据 y _j 的响应度。

 

3. 确定EM算法的M步

迭代的M步是求函数Q对theta的极大值，即求新一轮迭代的模型参数

通过求偏导并令其为0和约束条件 可得，

 

9.4  EM算法的推广

EM算法还可以解释为F函数(F function)的极大-极大算法(maximization- maximization  algorithm)，基于这个解释有若干变形与推广，如广义期望极大 (generalized expectation maximization,  GEM)算法。

 F函数的极大-极大算法

定义9.3 (F函数) 假设隐变量数据Z的概率分布为 P ^~(Z)，定义分布  P ^~  与 参数theta 的函数F(   P ^~   ,theta ） 如下

成为F函数，其中H是分布   P ^~ (Z) 的熵。

引理9.1 对于固定的 theta ，存在唯一的分布 P ^~ (theta) 极大化F，这时 P ^~ (theta) 由下式 给出:

并且 P ^~ (theta) 随 theta 连续变化.

 

定理9.3 设L(theta)=P(Y | theta)为观测数据的对数似然函数，theta⁽ⁱ⁾,i=1,2,... 为EM算法得到的参数估计序列，如果函数

F(P^~ ,theta)在户P^~*和theta^*有局部极大值，那么L(theta)也在theta^*有局部极大值。类似地，如果F在P^~*和theta^*达到全局最大值，那么L也在theta^*达到全局最大值。

定理9.4   EM算法的一次迭代可由F函数的极大-极大算法实现。

    设 theta ⁽ⁱ⁾ 为第i次迭代参数 theta 的估计， P ^~(i) 为第i次迭代函数 P ^~ 的估计。在第i+1 次迭代的两步为

    (1) 对固定的 theta ⁽ⁱ⁾ ，求 P ^~(i+1) 使F( P ^~ , theta ⁽ⁱ⁾ ) 极大化

    (2) 对固定的 P ^~(i+1) ， 求 theta ⁽ⁱ⁺¹⁾ 使F( P ^~(i+1) , theta ) 极大化

通过以上两步完成了EM算法的一次迭代。 由此可知， 由EM算法与F函数的极 大-极大算法得到的参数估计序列 是一 致的。

EM算法的推广--GEM算法

   

在GEM算法1中，有时求Q( theta ， theta ⁽ⁱ⁾ )的极大化是很困难的。

GEM 算法2和GEM算法3并不是直接求 theta ⁽ⁱ⁺¹⁾ 使Q达到极大的 theta ，而是找一个 theta ⁽ⁱ⁺¹⁾ 使得Q( theta ⁽ⁱ⁺¹⁾ , theta ⁽ⁱ⁾ ) > Q( theta ⁽ⁱ⁾ , theta ⁽ⁱ⁾ )

当参数 theta 的维数为d(d>=2)时，可采用一种特殊的GEM算法，它将EM 算法的M步分解为d次条件极大化，每次只改变参数向量的一个分量，其余分 量不改变。

GEM算法的特点是每次迭代增加F函数值(并不一定是极大化F 函数)，从而增加似然函数值。

 

来自为知笔记(Wiz)

转载于:https://www.cnblogs.com/YongSun/p/4767517.html