最大流问题——Ford-Fulkerson方法的java实现

使用的图的数据结构是邻边哈希表，见Graph源码。

package algorithm;

import java.util.LinkedList;
import java.util.List;
import java.util.Queue;

import matrix.Graph;

public class MaxFlow {

	/**
	 * 定义最后结果的结构： 源节点、汇节点、最大流量、产生流量的通路
	 */
	public int sink, source;
	public double maxFlow;
	public List<UnblockedPath> paths = new LinkedList<>();

	public MaxFlow(int s, int t) {
		source = s;
		sink = t;
	}

	/**
	 * 可增广路径： 指流量未达到饱和的从源到汇的路径，增加该路径的流量使总流量增大
	 */
	static class UnblockedPath {
		public boolean found = false; // 是否找到可增广路径
		public int[] preNodes = null; // 用于回溯从终点到起点的路径
		public double flow = 0; // 该路径上的流量
	}

	/**
	 * 用广度优先的搜索方式，找到可增广路径后立刻返回
	 * 
	 * @param g
	 *            最大流问题所在的图
	 * @param source
	 *            源节点
	 * @param sink
	 *            汇节点
	 * @return 找到一条可增广路径
	 */
	public static UnblockedPath findUnblockedPath(Graph g, int source, int sink) {
		UnblockedPath ubp = new UnblockedPath();

		// 初始化回溯节点
		ubp.preNodes = new int[g.getNodeNum()];
		ubp.preNodes[source] = -1;

		// 初始化源节点的最大可行流
		boolean[] visited = new boolean[g.getNodeNum()];

		Queue<Integer> queue = new LinkedList<>();
		queue.offer(source);
		while (!queue.isEmpty()) {
			int currentNode = queue.poll();
			visited[currentNode] = true;

			// 如果找到了一条通向终点的路径，立即返回
			if (currentNode == sink) {
				ubp.found = true;
				break;
			}

			// 将当前节点的出边相连的下一节点加入搜索队列，并记录前驱
			for (Integer nextNode : g.getOutEdges(currentNode).keySet()) {
				if (!visited[nextNode] && g.getEdge(currentNode, nextNode) > 0) {
					ubp.preNodes[nextNode] = currentNode; // 记录前驱
					queue.offer(nextNode);
				}
			}
		}
		return ubp;
	}

	/**
	 * 每次找到可增广路径后，将该路径的流量增至最大，修改路径上的边的容量，循环直到没有可增长路径，对应流量最大值
	 * 
	 * @param g
	 *            最大流问题所在的图
	 * @param source
	 *            源节点
	 * @param sink
	 *            汇节点
	 * @return 最大流问题的解
	 */
	public static MaxFlow FordFulkerson(Graph g, int source, int sink) {
		MaxFlow mf = new MaxFlow(source, sink);
		double increment = Graph.INF;
		while (true) {
			UnblockedPath ubp = findUnblockedPath(g, source, sink);
			if (!ubp.found) {
				break;
			}

			// 回溯的终点
			int end = ubp.preNodes[source];

			// 计算路径 ubp 上的流量，即总流量的增量
			int temp = sink;
			while (ubp.preNodes[temp] != end) {
				increment = Math.min(increment, g.getEdge(ubp.preNodes[temp], temp));
				temp = ubp.preNodes[temp];
			}
			// 保存结果
			ubp.flow = increment;
			mf.maxFlow += increment;
			mf.paths.add(ubp);

			// 更新容量
			temp = sink;
			while (ubp.preNodes[temp] != end) {
				g.addEdge(ubp.preNodes[temp], temp, g.getEdge(ubp.preNodes[temp], temp) - increment);
				g.addEdge(temp, ubp.preNodes[temp], g.getEdge(temp, ubp.preNodes[temp]) + increment);
				temp = ubp.preNodes[temp];
			}
			// g.show();

		}

		return mf;
	}

	/**
	 * 结果展示
	 */
	public void analyse() {
		System.out.println("source  : " + source);
		System.out.println("sink    : " + sink);
		System.out.println("maxFlow : " + maxFlow);
		for (UnblockedPath ubp : paths) {
			int temp = sink;
			int end = ubp.preNodes[source];
			System.out.print(ubp.flow + "\t: ");
			while (ubp.preNodes[temp] != end) {
				System.out.print(temp + " => ");
				temp = ubp.preNodes[temp];
			}
			System.out.println(source);
		}
	}
}

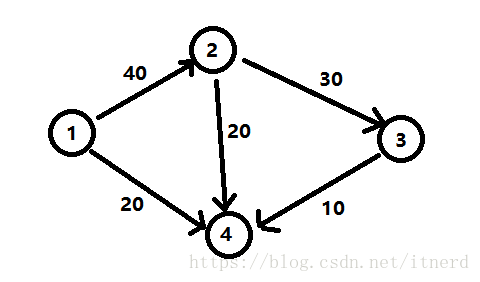
来看一个小例子：

1 为源节点， 4为汇节点， 求1到4的最大流。

	public static void main(String[] args) {
		Graph g = new Graph(5, false); // 有向图
		g.setDefaultValue(0.0); // 默认值为0，用零容量来表示不存在的边
		double[][] triples = { 
				{ 1, 2, 40 }, 
				{ 1, 4, 20 }, 
				{ 2, 4, 20 }, 
				{ 2, 3, 30 }, 
				{ 3, 4, 10 } 
			};
		g.addEdges(triples);
		g.show();

		MaxFlow mf = MaxFlow.FordFulkerson(g, 1, 4);
		mf.analyse();
	}

运行结果为：

0.0 0.0 0.0 0.0 0.0 
0.0 0.0 40.0 0.0 20.0 
0.0 0.0 0.0 30.0 20.0 
0.0 0.0 0.0 0.0 10.0 
0.0 0.0 0.0 0.0 0.0 
source  : 1
sink    : 4
maxFlow : 50.0
20.0	: 4 <= 2 <= 1
20.0	: 4 <= 1
10.0	: 4 <= 3 <= 2 <= 1

最后摘录一段非常精炼的cpp代码，以备参考。

/*****************************************
* 这段代码太TM精炼了，何忍不抄！！！ 
******************************************/
#include  
#include  
#include  
#include  
using namespace std; 
int map[300][300]; 
int used[300]; 
int n,m; 
const int INF = 1000000000; 
int dfs(int s,int t,int f) { 
  if(s == t) return f; 
  for(int i = 1 ;i <= n ; i ++) { 
    if(map[s][i] > 0 && !used[i]) { 
      used[i] = true; 
      int d = dfs(i,t,min(f,map[s][i])); 
      if(d > 0) { 
        map[s][i] -= d; 
        map[i][s] += d; 
        return d; 
      } 
    } 
  } 
} 
int maxflow(int s,int t) { 
  int flow = 0; 
  while(true) {
    memset(used,0,sizeof(used)); 
    int f = dfs(s,t,INF);//不断找从s到t的增广路 
    if(f == 0)
    return flow;//找不到了就回去 
    flow += f;//找到一个流量f的路 
  } 
} 
int main() {
while(scanf("%d%d",&m,&n) != EOF) { 
  memset(map,0,sizeof(map)); 
    for(int i = 0; i < m ; i ++) { 
      int from,to,cap; 
      scanf("%d%d%d",&from,&to,&cap);
      map[from][to] += cap; 
    } 
    cout << maxflow(1,n) << endl; 
  } 
  return 0; 
}