二叉搜索树详解——附加C语言代码实现

二叉搜索树：

对于树中的每个节点X，它的左子树中所有项的值都小于X，右子树所有值都大于X，并且没有重复。

一、构造树：

树可以由一个个的节点构成，所以先定义节点结构体，和数据类型变量重命名

typedef int BSTDataType;

typedef struct BSTreeNode
{
	struct BSTreeNode* _left;
	struct BSTreeNode* _right;

	BSTDataType _data;
}BSTreeNode;

 

二、插入节点：

每插入一个节点的时候，与当前节点判断，如果比当前节点大，就往右插入（右边没有节点的情况下），否则往左边插入。如果左右都有子节点，则继续进行比较。

代码：

//插入
int BSTreeInsert(BSTreeNode** tree, BSTDataType x)
{	//注意要传入二级指针，因为tree的跟可能不存在，不存在的话一级指针访问就会出现错误
	BSTreeNode* cur, *parent;
	if (*tree == NULL)	//如果是空树，就创建一个根返回（1表示成功）
	{
		*tree = BuyBSTreeNode(x);
		return 1;
	}

	cur = *tree;//cur指向根节点
	parent = NULL;
	while (cur)	//cur指向当前节点，当前节点不为空时，x如果大于当前值就往右走，小于就往左走
	{
		if (cur->_data >x)
		{
			parent = cur;
			if (cur->_left)
			{
				cur = cur->_left;
			}
			else
			{
				break;
			}
		}
		else if (cur->_data < x)
		{
			parent = cur;
			if (cur->_right)
			{
				cur = cur->_right;
			}
			else
			{
				break;
			}
		}
		else//否则就是存在相同的，无法插入，返回0
		{
			return 0;
		}
	}

	//走到这里，cur已经为空，说明可以插入了，就按定义插入
	if (parent->_data < x)
	{
		parent->_right = BuyBSTreeNode(x);
	}
	else
	{
		parent->_left = BuyBSTreeNode(x);
	}

	return 1;//插入成功
}

//创建节点（辅助插入）
BSTreeNode* BuyBSTreeNode(BSTDataType x){
	BSTreeNode* pbst = (BSTreeNode*)malloc(sizeof(BSTreeNode));
	pbst->_data = x;
	pbst->_left = NULL;//注意要把左右孩子置空，否则后面的while循环受影响
	pbst->_right = NULL;
	return pbst;
}

三、销毁树：

//2.销毁（递归实现）
void BSTreeDestory(BSTreeNode** tree)//销毁树
{
	if (tree == NULL)//非法操作
		return;
	if (*tree == NULL)//空树
		return;
	BSTreeNode* root = *tree;
	BSTreeDestory(&root->_left);
	BSTreeDestory(&root->_right);
	BSTreeDestory(root);
	*tree = NULL;
	return;
}

四、查找（搜索二叉树之所以这样创建，就是因为查找效率高）：

//查找
BSTreeNode* BSTreeFind(BSTreeNode** tree, BSTDataType x)
{
	BSTreeNode* cur = *tree;//当前节点cur指向根节点
	while (cur)
	{
		//只要当前节点不为空，就根据定义往左往右找。
		if (cur->_data < x)
		{
			cur = cur->_right;
		}
		else if (cur->_data > x)
		{
			cur = cur->_left;
		}
		else//不大不小就找到了
		{
			return cur;
		}
	}
	return NULL;
}

 

五、递归的方式插入、查找：

// 递归插入
int BSTreeInsertR(BSTreeNode** tree, BSTDataType x)
{
	BSTreeNode* cur = *tree;

	//如果x大于当前节点，就去右子树插入
	if (x > cur->_data)
	{
		//如果右正好是空的，直接插入
		if (cur->_right == NULL)
		{
			
			cur->_right = BuyBSTreeNode(x);
		}
		//否则去右子树里继续想办法插入
		else
		{
			return BSTreeInsertR(cur->_right, x);
		}
	}
	//如果x小于当前节点，就去左子树插入
	else if (x < cur->_data)
	{
		if (cur->_left == NULL)//左孩子正好空
		{
			cur->_left = BuyBSTreeNode(x);
		}
		else//否则就去左子树插入
		{
			return BSTreeInsertR(cur->_left, x);
		}
	}
	else
	{
		return 0;//存在相同无法插入
	}
}

//递归查找
const BSTreeNode* BSTreeFindR(BSTreeNode** tree, BSTDataType x)
{
	BSTreeNode* cur = *tree;
	//大于就去右子树找，小于就去左子树找
	if (x > cur->_data)
	{
		return BSTreeFindR(cur->_right, x);
	}
	else if (x < cur->_data)
	{
		return BSTreeFindR(cur->_left, x);
	}
	else
	{
		return cur;//找到了
	}
}

 

六、删除操作：

删除操作比较复杂，主要复杂在，要考虑到所有的情况。下面依次介绍节点的4种情况：

• 无左子树，无右子树。
• 无左子树，有右子树。
• 有左子树，无右子树。
• 既有左子树，也有右子树。

删除步骤：

1、首先要找到删除的节点和他的父节点（如果传入的是要删除的值）

2、判断他是父亲的左节点还是右节点

3、判断他是什么类型的节点，从而对应的删除节点：

（1）叶子节点（无孩子）：根节点直接删除，如果有父亲，就断开父亲的左（右）指针就可以再free。

（2）存在一个孩子的节点：

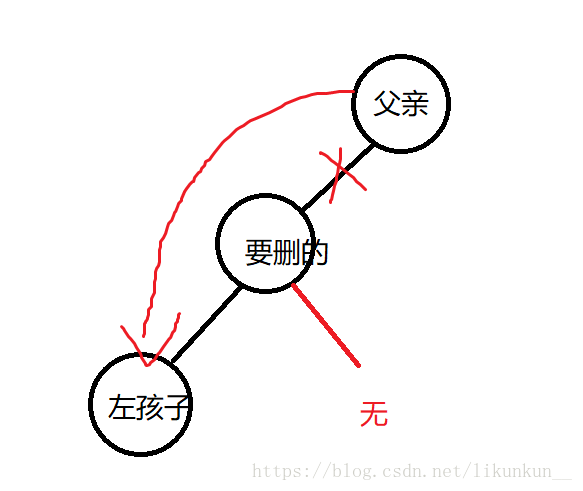
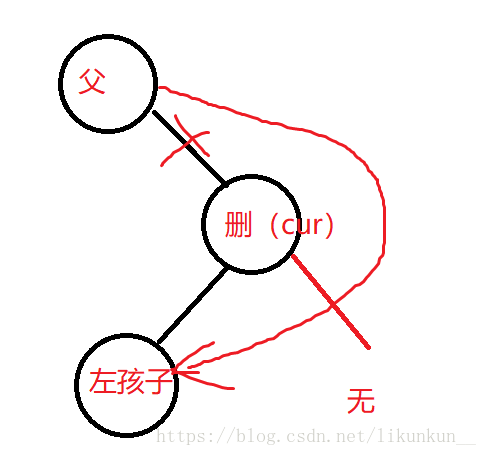
        1>存在左孩子：如果cur是父亲的左节点，就用父亲的左指针指向cur的左孩子，相当于跳过cur接上去。如果是右节                                                点就是把父亲的右指针指向cur的左孩子。

        2>存在右孩子：和上面一样的，把父亲的对应左（右）指针，指向cur的右孩子。这就是前面判断cur是父亲的左右的作用。

（3）含有两个孩子：因为搜索二叉树的性质是：任何一个节点，他的左子树中所有项的值都小于它，右子树所有值都大于X。所以我们需要在他的左子树和右子树里找一个比左子树的全部大，但比右子树的全部小的节点。也就是左子树的最大节点，或者右子树的最小节点。我们把它叫做后继节点。

也就是，左孩子一直往右走到底，或者右孩子一直往左走到底。这两个节点都可以作为代替删除的节点。

代替的时候，记得要：

（1）断开后继的父亲：断开8.5（7.5）和父节点的连接。

（2）后继连上原位置的左右：8.5的左右指针要连上8的左右。

（3）原节点的父节点要连上后继节点：6的右指针要连上8.5.

至此，所有情况都考虑完了。

代码：

//删除一个点，成功返回1，否则返回0
int BSTreeRemove(BSTreeNode** tree, BSTDataType x)
{
	//定义当前节点和父节点
	BSTreeNode *parent, *cur;
	cur = *tree;
	parent = *tree;

	//定义当前节点是他的父节点的左节点还是右节点,1为左
	int isleft = 1;

	//找到要删除的点和他的父节点
	while (cur->_data != x)
	{
		parent = cur;
		if (cur->_data > x)
		{
			cur = cur->_left;
			isleft = 1;
		}
		else
		{
			cur = cur->_right;
			isleft = 0;
		}

		if (cur == NULL)
		{
			printf("没有该节点");
			return 0;
		}
	}
	//寻找结束，cur指向要删除节点，parrent指向他的父节点，isleft = 1说明cur是parrent的左节点。

	//开始删除
	//1、是叶子节点
	if (cur->_left == NULL && cur->_right == NULL)
	{	
		//（1）如果是根节点直接删除
		if (cur == *tree)
		{
			cur = NULL;
			free(cur);
		}
		//（2）如果是左边就parrent->left = null ; free(left);
		else if (isleft)
		{
			parent->_left = NULL;
			free(cur);
		}
		//（3）如果是右边就删右边
		else
		{
			parent->_right = NULL;
			free(cur);
		}
	}
		


	//2、是带有一个子节点的节点
	//（1）带有的是左节点：
	else if (cur->_right == NULL)
	{
		//1>删除的节点是根，把左节点变成跟
		if (*tree == cur)
		{
			*tree = cur->_left;
			free(cur);
		}
		//2>删除的节点是parent的左节点，把parent的左指针指向cur的左节点。free(now)
		else if (isleft)
		{
			parent->_left = cur->_left;
			free(cur);
		}
		//3>是parent的右节点，把parent的右指针指向now的左节点。free(now)
		else
		{
			parent->_right = cur->_left;
			free(cur);
		}
	}

	//（2）带有的是右节点：
	else if (cur->_left == NULL)
	{
		//1>删除根，把右节点变成根
		if (*tree == cur)
		{
			*tree = cur->_right;
			free(cur);
		}
		//2>删的是p的左节点，把p的左接上now的右
		else if (isleft)
		{
			parent->_left = cur->_right;
			free(cur);
		}
		//3>删p的右，把p的右接上now的右节点
		else
		{
			parent->_right = cur->_right;
			free(cur);
		}
	}
		
			

	//3、删除有两个子节点的节点
	//寻找中序后继节点替换删除的节点，后继节点为，比删除节点大，但比他的右子树的任何一个节点都小（先右走，在一直坐走到底）
	else
	{
		//寻找后继节点的时候，要吧他从父亲那断开
		BSTreeNode* houji = getHouji(cur);

		//1>删除根，把后继节点变成根
		if (*tree == cur)
		{
			houji->_left = cur->_left;
			houji->_right = cur->_right;
			free(cur);
		}
		//2>删的是p的左节点，把p的左接上后继节点
		else if (isleft)
		{
			parent->_left = houji;
			houji->_left = cur->_left;
			houji->_right = cur->_right;
			free(cur);
		}
		//3>删p的右，把p的右接上后继节点，
		else
		{
			parent->_right = houji;
			houji->_left = cur->_left;
			houji->_right = cur->_right;
			free(cur);
		}
	}

}

//寻找中序后继节点
BSTreeNode* getHouji(BSTreeNode* del)
{
	//寻找后继节点的时候，要吧他从父亲那断开
	BSTreeNode* parrent = del;
	BSTreeNode *now = del;
	BSTreeNode *houji = del->_right;
	
	if (!houji->_left)
	{
		parrent->_right = NULL;
	}
	else
	{
		while(houji->_left)
		{
			parrent = houji;
			houji = houji->_left;
		}
		parrent->_left = NULL;
	}
	return houji;
}