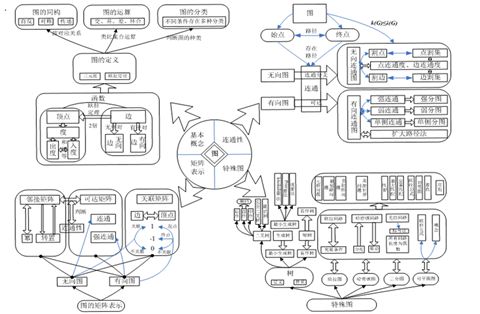
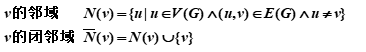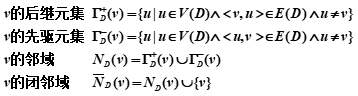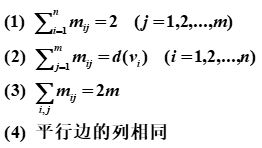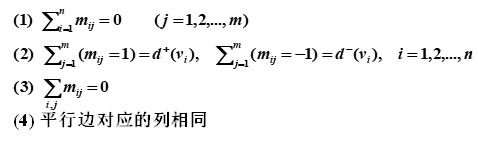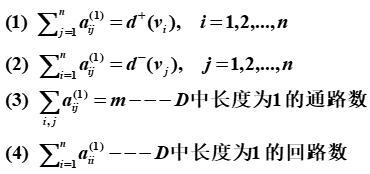离散数学-14 图的基本概念

相关概念

1. 图

① 可用G泛指图（无向的或有向的）

②V(G), E(G), V(D), E(D)

③ n阶图

2. 有限图

3. n 阶零图（无边图，孤立结点构成）与平凡图（一阶零图，只有一个顶点，没有边）

4. 空图——（顶点集为空集）

5. 用 e_k 表示无向边或有向边

6. 顶点与边的关联关系

① 关联、关联次数

② 环（伪图：含有环的图）

③ 孤立点（没有边关联的顶点）

7. 顶点之间、边之间的相邻与邻接关系

8. 邻域与关联集

①vV(G) (G为无向图)

v 的关联集

②vV(D) (D为有向图)

9. 标定图与非标定图

10. 基图（有向图化无向图）

预备知识

• 多重集合——元素可以重复出现的集合
• 无序集——AB={(x,y) | xAyB}

定义14.1无向图G = <V,E>, 其中

(1) V 为顶点集，元素称为顶点

(2) E为VV 的多重子集，其元素称为无向边，简称边

定义14.2有向图D=<V,E>, 只需注意E是VV 的多重子集

定义14.3

(1) 无向图中的平行边及重数（平行边的条数）

(2) 有向图中的平行边及重数（注意方向要相同，一定要相同起点、终点）

(3) 多重图（含平行边的图）

(4) 简单图（不含平行边也不含环的图）

在定义14.3中定义的简单图是极其重要的概念

定义14.4

(1) 设G=<V,E>为无向图, vV, d(v)——v的度数, 简称度（v作为边的端点的次数）

(2) 设D=<V,E>为有向图, vV,

d⁺(v)——v的出度（v作为边的始点的次数）

d^(v)——v的入度（v作为边的终点的次数）

d(v)——v的度或度数

(3) (G)最大度, (G)最小度

(4) ⁺(D), ⁺(D), ^(D), ^(D), (D), (D)

(5) 奇度顶点（度为奇数的顶点）与偶度顶点（度为偶数的顶点）

(6)悬挂顶点（度数为1的顶点），悬挂边

  

推论 任何图 (无向或有向) 中，奇度顶点的个数是偶数.

证明：(⟶) 握手定理 (←) 奇数度点两两之间连一边, 剩余度用环来实现.

定理14.4 设G为任意n阶无向简单图，则0 (G)  n-1.(可简单图化必要条件)

Havel定理(可简单图化充要条件)

• 定理(V. Havel, 1955):设非负整数列d=(d₁,d₂,…,d_n)满足:d₁+d₂+…+d_n=0(mod 2),

  n-1d₁d₂…d_n0,则d可简单图化当且仅当 d'=(d₂-1,d₃-1,…,d_d1+1-1,d_d1+2,…,d_n)时可简单图化. 例: d=(4,4,3,3,2,2), d'=(3,2,2,1,2)依次类推。

  

  定义14.5设G₁=<V₁,E₁>, G₂=<V₂,E₂>为两个无向图(两个有向图)，若存在双射函数f:V₁V₂, 对于v_i,v_jV₁, (v_i,v_j)E₁ 当且仅当 (f(v_i),f(v_j))E₂（<v_i,v_j>E₁ 当且仅当 <f(v_i),f(v_j)>E₂ )并且, (v_i,v_j)（<v_i,v_j>）与 (f(v_i),f(v_j))（<f(v_i),f(v_j)>）的重数相同，则称G₁与G₂是同构的，记作G₁G₂.

• 图之间的同构关系具有自反性、对称性和传递性.
• 能找到多条同构的必要条件，但它们全不是充分条件：

  ① 边数相同，顶点数相同; ② 度数列相同;

  ③ 对应顶点的关联集及邻域的元素个数相同，等等

  若破坏必要条件，则两图不同构

• 判断两个图同构是个难题，（1）从定义入手；（2）构造双射函数（顶点和边一一对应）。

  

  定义14.6

  

  

  定义14.7如果无向简单图G的所有顶点具有相同的度数，则称图G为正则图。图中所有结点的度数为k的正则图记作k-正则图。

  

  K_n是 n1正则图，彼得松图（见书上图14.3所示，记住它）

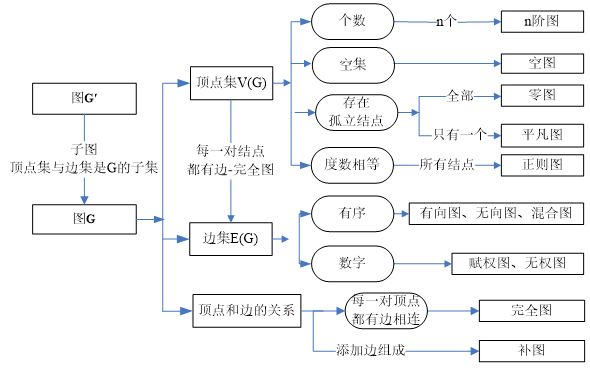
  定义14.8G=<V,E>, G=<V,E>

  (1) GG —— G为G的子图，G为G的母图

  (2) 若GG且V=V，则称G为G的生成子图

  (3) 若VV或EE，称G为G的真子图

  (4) 顶点集VV且V，并以G中两个端点都在V中的边组成边集E'，称之为G的V'的导出子图，记作G[V]

  (5) 边集EE且E，并以E'中关联的顶点为顶点集V'，称之为G的E'的导出子图，记作G[E]

  

  

  

  定义14.10删除边、删除顶点、收缩、加新边

  定义14.11给定图G=<V,E>（无向或有向的），G中顶点与边的交替序列 =v₀e₁v₁e₂…e_lv_l，v_i1, v_i 是 e_i 的端点.【用的杨炳儒本的概念】

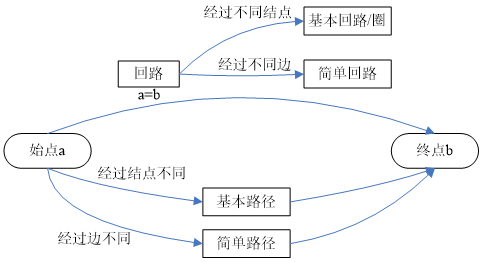
  (1) 路径与回路：为路径（通路）；若 v₀=v_l，为回路，l 为回路长度.

  (2) 简单路径（迹）与简单回路：所有边各异，为简单路径（迹），又若v₀=v_l，为简单回路

  (3) 基本路径(轨)与基本回路(圈)：中所有顶点各异，则称为基本路径(轨)，又若除v₀=v_l，所有的顶点各不相同，则称为基本回路(圈)

  (4) 复杂路径与回路：有边重复出现

  

  定理 在具有n个结点的图中，若从结点v_j到结点v_k存在一条路径，则从结点v_j到结点v_k存在一条不多于n−1条边的路径。

  推论在具有n个结点的圈中，若从结点v_j到结点v_k存在一条路径，则从结点v_j到结点v_k存在一条不多于n条边的路径。

  长度相同的圈都是同构的，因此在同构意义下给定长度的圈只有一个。

  在标定图中，圈表示成顶点和边的标记序列。只要有两个标记序列不同，就认为这两个圈不同，称这两个圈在定义意义下不同。

  

  距离满足以下性质：

  1）d（ u, u）= 0；

  2）d（ u,v ）≥0；

  3）d（ u,w）+ d（w ,v）≥ d（u,v ）（三角不等式）

  注意：为了区别无向图中距离表示d(vi,vj)，有向图中距离表示d

  

  无向图的连通性

  (1) 顶点之间的连通关系：G=<V,E>为无向图

  ① 若 v_i 与 v_j 之间有通路，则 v_iv_j

  ② 是V上的等价关系 R={<u,v>| u,v V且uv}

  (2) G的连通性与连通分支

  ① 若u,vV，uv，则称G连通

  ② V/R={V₁,V₂,…,V_k}，称G[V₁], G[V₂], …,G[V_k]为连通分支，其个数 p(G)=k (k1)； k=1，G连通

  (3) 短程线与距离

  ① u与v之间的短程线：uv，u与v之间长度最短的通路

  ② u与v之间的距离：d(u,v)——短程线的长度

  ③ d(u,v)的性质：

  d(u,v)0, u≁v时d(u,v)=

  d(u,v)=d(v,u)

  d(u,v)+d(v,w)d(u,w)

  1. 删除顶点及删除边

  Gv ——从G中将v及关联的边去掉

  GV——从G中删除V中所有的顶点

  Ge ——将e从G中去掉

  GE——删除E中所有边

  2. 点割集与边割集

  点割集与割点

  

  定义14.16G=<V,E>, VV

  V为点割集——p(GV)>p(G)且有极小性

  v为割点——{v}为点割集

  定义14.17G=<V,E>, EE

  E是边割集——p(GE)>p(G)且有极小性

  e是割边（桥）——{e}为边割集

  

  

    

  定义14.18G为连通非完全图

  点连通度—(G) = min{ |V |V 为点割集 }

  (G)是使G不连通需要删去的最少的结点数。

  规定 (K_n) = n1

  若G非连通，(G) = 0

  若 (G)k，则称G为 k-连通图

  定义14.19 设G为连通图

  边连通度——(G) = min{|E|E为边割集}

  若G非连通，则(G) = 0

  若(G)r，则称G是 r 边-连通图

  定理7.5(G)(G)(G)

  定义14.20D=<V,E>为有向图

  v_i v_j（v_i 可达 v_j）——v_i 到v_j 有通路

  v_i v_j（v_i 与v_j 相互可达）

  性质

  具有自反性(v_i v_i)、传递性

  具有自反性、对称性、传递性

  定义14.22D=<V,E>为有向图

  D弱连通(连通)——基图为无向连通图

  D单向连通——v_i,v_jV，v_iv_j 或 v_jv_i

  D强连通——v_i,v_jV，v_iv_j

  易知，强连通Þ单向连通Þ弱连通

  判别法

  定理14.8D强连通当且仅当D中存在经过每个顶点至少一次的回路

  定理14.9D单向连通当且仅当D中存在经过每个顶点至少一次的通路

  无向图中

  设G=<V,E>为 n 阶无向图，E. 设 _l 为G中一条路径，若此路径的始点或终点与通路外的顶点相邻，就将它们扩到通路中来，继续这一过程，直到最后得到的通路的两个端点不与通路外的顶点相邻为止. 设最后得到的路径为_l+k（长度为 l 的路径扩大成了长度为 l+k 的路径），称_l+k为"极大路径"，称使用此种方法证明问题的方法为"扩大路径法".

  定义14.23设G=<V,E>为一个无向图，若能将 V分成 V₁和V₂(V₁V₂=V，V₁V₂=)，使得 G 中的每条边的两个端点都是一个属于V₁，另一个属于V₂，则称 G 为二部图 ( 或称二分图、偶图等 )，称V₁和V₂为互补顶点子集，常将二部图G记为<V₁,V₂,E>. 又若G是简单二部图，V₁中每个顶点均与V₂中所有的顶点相邻，则称G为完全二部图，记为 K_r,s，其中r=|V₁|，s=|V₂|.

  注意，n 阶零图为二部图.

  定理14.10无向图G=<V,E>是二部图当且仅当G中无奇圈

  无向图的关联矩阵（对图无限制）

  定义14.24无向图G=<V,E>，|V|=n，|E|=m，令 m_ij为 v_i 与 e_j

  的关联次数，称(m_ij)_nm为G 的关联矩阵，记为M(G).

  性质

  

  定义14.25有向图D=<V,E>，令

  

  则称 (m_ij)_nm为D的关联矩阵，记为M(D).

  性质

  

  定义14.26设有向图D=<V,E>, V={v₁, v₂, …, v_n}, E={e₁, e₂, …, e_m}, 令a_ij为顶点 v_i 邻接到顶点 v_j 边的条数，称为D的邻接矩阵，记作A(D)，或简记为A.

  性质

  

  定理14.11设A为有向图 D 的邻接矩阵，V={v₁, v₂, …, v_n}为顶点集，则 A 的 l 次幂 A^l（l1）中元素

  

    

  

  定义14.27设D=<V,E>为有向图. V={v₁, v₂, …, v_n}, 令

  

  称 (p_ij)_nn 为D的可达矩阵，记作P(D)，简记为P.

""。

  

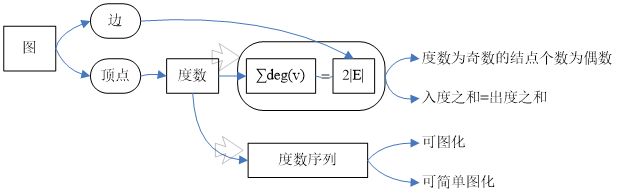
握手

定理

  

图的度数列

1 . V={v₁, v₂, …, v_n}为无向图G的顶点集，称d(v₁), d(v₂), …, d(v_n)为G的度数列

2. V={v₁, v₂, …, v_n}为有向图D的顶点集，

D的度数列：d(v₁), d(v₂), …, d(v_n)

D的出度列：d⁺(v₁), d⁺(v₂), …, d⁺(v_n)

D的入度列：d^(v₁), d^(v₂), …, d^(v_n)

3. 非负整数列d=(d₁, d₂, …, d_n)是可图化的（有图对应度数列）?是可简单图化（有简单图对应度数列）的?