最小费用最大流问题与算法实现（Bellman-Ford、SPFA、Dijkstra）

摘要

今日，对最小费用最大流问题进行了一个简单的研究，并针对网上的一些已有算法进行了查找和研究。博客和资料很多，但是留下的算法很多运行失败、出错，或者意义不明。这里，个人对其中的Bellman-Ford、SPFA、改进的Dijkstra三种应用于最小费用最大流的算法进行了实现，经过测试，确保其可行性。

网络流

关于网络流，这里引入几个概念：

• 源点：有n个点，有m条有向边，其中有一个点比较特殊，它只出不进，即入度为0。这样的点我们称为源点，一般用字母S表示。
• 汇点：另一个点也比较特殊，只进不出，即出度为0。这样的点我们称为汇点，一般用字母T表示。
• 容量和流量：每条有向边上有两个量，容量和流量，从i到j的容量表示为c[i,j]表示，流量则用f[i,j]表示。

通常来说，我们可以将这些边具象成道路，流量就是这条道路上的车的容量，容量就是道路可以承受的最大的车流量。
很明显，流量≤容量。
而对于每个不是源点和汇点的节点而言，可以类比为没有存储功能的货物的中转站。所有进入他们的流量等于所有从它出来的流量。

• 最大流：把源点比作工厂的话，问题就是求工厂最大可以发出多少货物，而不至于超过道路的容量限制，也即，最大流问题。

求解思路：
首先，假如所有边上额流量都不超过容量，那么我们就把这一组流量，或者说，这个流，称为一个可行流。
一个最简单的可行流的例子就是零流，即所有的流量都是0的流。

1. 我们从这个零流开始考虑，假如有这样一条路径，这条路从原点开始一直一段一段的连接，就可以到达汇点。并且，这条路径上的每一段都会满足流量＜容量（注意，不是≤，而是严格＜）
2. 那么，我们就一定可以找到这条路径上的每一段的（容量-流量）的值中的最小值delta。我们把这条路上的每一段的流量都加上这个delta，就一定可以保证目前这个流依然是可行流。
3. 这样，我们就找到了一个更大的流，它的流量是之前的流量+delta，而这条路径就称为增广路径。我们不断地从起点开始寻找增广路径，每次都对其进行增广，直到源点和汇点不再连通，也就是找不到增广路径为止。
4. 当我们找不到增广路径时，当前的流量就是最大流。

补充：

1. 寻找增广路径的时候我们可以简单的从原点开始做BFS，并不断修改这条路上的delta量，直到找到汇点或者找不到增广路径为止。
2. 在程序实现的过程中，我们通常只是使用一个c数组来记录容量，而不是记录流量。当流量+delta时，我们可以通过容量-delta来实现，以方便程序编写。

增加反向边的目的：
在做增广路径时可能会阻塞后来的增广路径，换计划说，做增广路径本来是有一个顺序的，只有按照有这一顺序，才能知道最大流。
但是我们在寻找时是任意的，为了修正，我们就每次讲流量加入到了反向弧中从而让后面的流能够进行自我的调整。

例子：

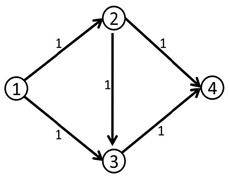
我们第一次，可以找到1-2-3-4这条增广路径，这条路径上的delta值显然为1。

此时，我们在修改之后得到了下面这个流。其中，边上的数字代表流量。

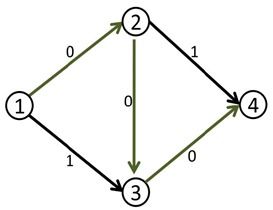
此时，边（1,2）和边（3,4）上的边就等于容量了，我们也再也找到不到其他的增广路径，于是，当前的流量是1。

然而，这个答案并不是最大流，因为我们可以同时走1-2-4和1-3-4，这样，可以得到流量为2的最大流。

之所以出现这样的问题，是因为我们在路径寻找的过程中，没有给一个“后悔”的机会，应该有一个不走2-3-4而改走2-4的机制。

而解决这个问题的办法，就是利用一种叫做反向边的概念来解决。
即每条边(i, j)都会有一条反向边(j,i)，反向边也同样有它的容量。

在第一次找到增广路径之后，在把路径上每一段容量减少delta的同时，也把每一段上的反方向的容量增加delta。

c[x,y]-=delta;
c[y,x]+=delta;

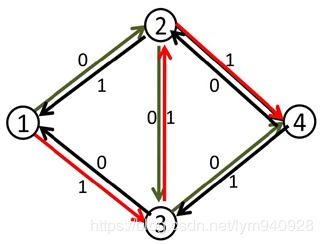
就上面这个例子，当我们找到1-2-3-4这条增广路径之后，将容量修改如下：

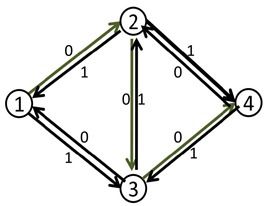
此时我们再去寻找增广路径，就可以得到一条：1-3-2-4，将这条路径增广之后，得到最大流为2.

这样为何有效？
实际上，当我们第二次的增广路径走3-2这条反向边时，就相当于把2-3这条正向边已经用的流量给“退”了回去，不走2-3这条路，从而改走从2点出发的其他的路径也即是2-4。

而如果这里没有2-4怎么办？
这时，假如没有2-4这条道路，那么最终这条增广路径在生成过程中也不会存在，因为最终它根本无法到达汇点。
同时，本来在3-4上的流量则是由1-3-4来“接管”。而最终2-3这条路径正向流量为1，反向流量也为1，等于没有流。

最小费用最大流

对一个费用容量网络，具有相同流量f的可行流中，总费用最小的可行流称为该费用容量网络关于流量f的最小费用流。简称为流量为f的最小费用流。

什么是最小费用最大流问题：
给定网络D=(V,A,C) 每一条弧(vi,vj)上，除了已给容量Cij外，还给了一个单位流量的费用b(vi,vj)>=0. 所谓最小费用最大流问题就是求一个最大流f，使流的总输送费用最小。

对于例子：

从S出发，到达T，正确路径结果，为：

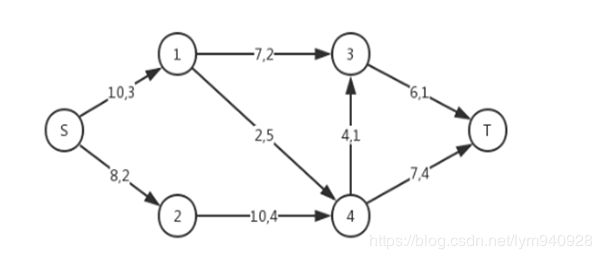
• S->1->3->T
• S->2->4->3->T
• S->2->4->5->T

最大流为10，最小费用为84。
以下算法在该图中测试，均可得出正确结果。

贝尔曼-福特算法（Bellman-Ford algorithm）

贝尔曼-福特算法（Bellman-Ford algorithm），是求解单元最短路径的一种算法。
它的基本原理是对图进行|V| - 1次松弛操作，得到所有可能的最短路径。
它比Dijkstra算法好的部分在于，在计算最短路径的班的权值可以为负，实现起来比较简单。
缺点则是时间复杂度较高，为O(|V||E|)。不过算法已经有了一些改进方案，比如队列优化的Bellmanford算法（SPFA算法），一定程度上提高了效率。

算法原理：
贝尔曼-福特算法与迪科斯彻算法类似，都以松弛操作为基础，即估计的最短路径值渐渐地被更加准确的值替代，直至得到最优解。
在两个算法中，计算时每个边之间的估计距离值都比真实值大，并且被新找到路径的最小长度替代。
然而，迪科斯彻算法以贪心法选取未被处理的具有最小权值的节点，然后对其的出边进行松弛操作；而贝尔曼-福特算法简单地对所有边进行松弛操作，共**|V| - 1**次。
在重复地计算中，已计算得到正确的距离的边的数量不断增加，直到所有边都计算得到了正确的路径。
因为算法可以使用负权值的边，因此贝尔曼-福特算法比迪科斯彻算法适用于更多种类的输入。

优化选项：

1. 循环的提前跳出
   在实际操作中，贝尔曼-福特算法经常会在未达到|V|-1前就给出解，|V|-1就是最大值。因此可以在循环中设置判定，在某次循环不再松弛时，直接退出循环，进行负权环判定。
2. 队列优化
   队列优化的贝尔曼-福特算法——SPFA算法基本思路与原算法是一样的，不过该算法的提升在于它不会盲目尝试所有的节点，而是维护一个备选节点队列，并且仅有节点被松弛之后才会放入到队列中。

代码实现：

#include "stdafx.h"
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 

#define MAXN 5050
#define INF 0x3f3f3f3f

using namespace std;

int n, m, s, t;
int u, v, c, w;
int maxFlow, minCost;

struct Edge
{
	int from, to, flow, cap, cost;
};

bool vis[MAXN];
int p[MAXN], a[MAXN], d[MAXN];
vector<int> g[MAXN];
vector<Edge> edges;

void init(int n)
{
	for (int i = 0; i <= n; i++)
		g[i].clear();
	edges.clear();
}
void addedge(int from, int to, int cap, int cost)
{
	Edge temp1 = { from, to, 0, cap, cost };
	Edge temp2 = { to, from, 0, 0, -cost };//允许反向增广
	edges.push_back(temp1);
	edges.push_back(temp2);
	int len = edges.size();
	g[from].push_back(len - 2);
	g[to].push_back(len - 1);
}

//贝尔曼-福特算法实现
bool bellmanford(int s, int t)
{
	for (int i = 0; i < MAXN; i++)
		d[i] = INF;
	d[s] = 0;
	memset(vis, false, sizeof(vis));
	memset(p, -1, sizeof(p));
	p[s] = -1;
	a[s] = INF;
	queue<int> que;
	que.push(s);
	vis[s] = true;
	while (!que.empty())
	{
		int u = que.front();
		que.pop();
		vis[u] = false;
		for (int i = 0; i < g[u].size(); i++)
		{
			Edge& e = edges[g[u][i]];
			if (e.cap > e.flow&&d[e.to] > d[u] + e.cost)//进行松弛，寻找最短路径也就是最小费用
			{
				d[e.to] = d[u] + e.cost;
				p[e.to] = g[u][i];
				a[e.to] = min(a[u], e.cap - e.flow);
				if (!vis[e.to])
				{
					que.push(e.to);
					vis[e.to] = true;
				}
			}
		}
	}
	if (d[t] == INF)
		return false;
	maxFlow += a[t];
	minCost += d[t] * a[t];
	for (int i = t; i != s; i = edges[p[i]].from)
	{
		edges[p[i]].flow += a[t];
		edges[p[i] ^ 1].flow -= a[t];
	}
	return true;
}


void MCMF()
{
	while (bellmanford(s, t))
		continue;
	return;
}


int _tmain(int argc, _TCHAR* argv[])
{
	
	cout << "节点数为："; cin >> n;
	cout << "边数为："; cin >> m;
	cout << "源点编号为："; cin >> s;
	cout << "汇点编号为："; cin >> t;

	cout << "输入 " << m << " 条边的信息：" << endl;
	while (m--)
	{
		cout << "起点："; cin >> u;
		cout << "终点："; cin >> v;
		cout << "容量："; cin >> c;
		cout << "费用："; cin >> w;
		cout << "-----------------" << endl;
		addedge(u, v, c, w);
	}

	MCMF();
	cout << "最大流为：" << maxFlow << endl;
	cout<< "最小费用为"<<minCost << endl;
	cout << endl;

	system("pause");
	return 0;

}

SPFA算法

算法描述：

1. 初始化：distance数组（从源点s到各点的最小费用）全部赋值为inf，用一个队列保存所有待松弛的顶点，初始时将s点放入队列中。
2. 队列+松弛操作：每次出队一个顶点u，对其所有的边进行松弛，如果存在某条边u->v松弛成功（dist(v)>dist(u)+w(u,v)），则将v加入队列中（当v不在队列时）；重复以上操作直到队列为空或者发现负权环。
   如果网络中存在负权回路，则算法永远都不会结束，陷入死循环。

• 判断是否存在负权环的方法：
  对任何一个顶点，每进入一次队列，意味着需要进行一次松弛，即如果某个顶点进入队列的次数超过V，说明存在负权环。

算法步骤：

1. 建立一个队列，将源点加入队列中，建立一个数组dist记录源点到所有点的最短路径（初始为inf，源点到本身的最短路径是0）。
2. 从队列中取出队头元素，刷新其连接的所有点的最短路径；如果刷新成功且被刷新点不在队列中，则把该点加入到队尾。
3. 重复执行以上步骤直到队列为空或者队列中存在负权环。

代码实现：

#include "stdafx.h"
#include
#include
#include
#include
#include

#define MAXN 5050

using namespace std;

bool vis[MAXN];
int n, m, s, t;
int u, v, c, w;
int cost[MAXN], pre[MAXN], last[MAXN], flow[MAXN];
int maxFlow, minCost;
struct Edge
{
	int from, to, flow, cost;
}edge[MAXN];

int head[MAXN], num_edge;

queue <int> q;

void addedge(int from, int to, int flow, int cost)
{
	edge[++num_edge].from = head[from];
	edge[num_edge].to = to;
	edge[num_edge].flow = flow;
	edge[num_edge].cost = cost;
	head[from] = num_edge;

	edge[++num_edge].from = head[to];
	edge[num_edge].to = from;
	edge[num_edge].flow = 0;
	edge[num_edge].cost = -cost;
	head[to] = num_edge;

}

bool SPFA(int s, int t)
{
	memset(cost, 0x7f, sizeof(cost));
	memset(flow, 0x7f, sizeof(flow));
	memset(vis, 0, sizeof(vis));
	q.push(s); vis[s] = 1; cost[s] = 0; pre[t] = -1;

	while (!q.empty())
	{
		int now = q.front();
		q.pop();
		vis[now] = 0;
		for (int i = head[now]; i != -1; i = edge[i].from)
		{
			if (edge[i].flow>0 && cost[edge[i].to]>cost[now] + edge[i].cost)
			{
				cost[edge[i].to] = cost[now] + edge[i].cost;
				pre[edge[i].to] = now;
				last[edge[i].to] = i;
				flow[edge[i].to] = min(flow[now], edge[i].flow);
				if (!vis[edge[i].to])
				{
					vis[edge[i].to] = 1;
					q.push(edge[i].to);
				}
			}
		}
	}
	return pre[t] != -1;
}

void MCMF()
{
	while (SPFA(s, t))
	{
		int now = t;
		maxFlow += flow[t];
		minCost += flow[t] * cost[t];
		while (now != s)
		{
			edge[last[now]].flow -= flow[t];
			edge[last[now] ^ 1].flow += flow[t];
			now = pre[now];
		}
	}
}


int _tmain(int argc, _TCHAR* argv[])
{	
	memset(head, -1, sizeof(head)); num_edge = -1;//初始化 

	
	cout << "节点数为："; cin >> n;
	cout << "边数为："; cin >> m;
	cout << "源点编号为："; cin >> s; 
	cout << "汇点编号为："; cin >> t; 

	cout << "输入 " << m << " 条边的信息：" << endl;
	while (m--)
	{
		cout << "起点："; cin >> u; 
		cout << "终点："; cin >> v; 
		cout << "容量："; cin >> c; 
		cout << "费用："; cin >> w; 
		cout << "-----------------" << endl;
		addedge(u, v, c, w);
	}

	MCMF();
	cout << "最大流为：" << maxFlow << endl;
	cout << "最小费用为：" << minCost << endl;
	cout << endl;
	
	system("pause");
	return 0;
}

改进的Dijkstra算法

算法描述：
用于求解指定两点间的最短路，或从指定点到其余个点的最短路。是目前求非负权网络最短路问题的最好方法。
基本步骤：

1. 将所有的顶点分成两个集合，P集合和Q集合，初始时P集合只有源点，其他顶点都在Q集合中。
2. 每次选择P集合中新加入的顶点u，用该顶点作为中转点更新Q集合中的顶点的最短路（松弛）；选择Q中最短路值最小的顶点加入到集合P中。
3. 重复步骤2直到集合Q中没有顶点。

由于最小费用最大流网络中存在负权值，Dijkstra算法不能直接求解最小费用最大流问题，如果最小费用最大流网络中的权值都非负，则可使用Dijkstra算法。引入势函数h(u)为上一次Dijkstra算法的dist(u)（表示从源点到顶点u的最短距离），对每一条边（u,v）,h(v)<=h(u)+w(u,v)成立，则下一次计算中dist(v)=dist(u)+w(u,v)+h(u)-h(v)，所有的dist值必然都大于等于0，则可以继续用Dijkstra算法求解最短路。

代码实现：

#include "stdafx.h"
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 

#define MAXN 5050
#define INF 0x3f3f3f3f
#define P pair

using namespace std;

struct edge
{
	int to, cap, cost, rev;
};

int n, m, s, t;
int u, v, c, w;
int maxFlow, minCost;

vector<edge> G[MAXN];
int h[MAXN];
int dist[MAXN], prevv[MAXN], preve[MAXN];

void addedge(int from, int to, int cap, int cost)
{
	edge temp1 = { to, cap, cost, (int)G[to].size() };
	edge temp2 = { from, 0, -cost, (int)G[from].size() - 1 };
	G[from].push_back(temp1);
	G[to].push_back(temp2);
}

//Dijkstra算法实现
void MCMF(int s, int t, int f)
{
	fill(h + 1, h + 1 + n, 0);
	while (f > 0)
	{
		priority_queue<P, vector<P>, greater<P> > D;
		memset(dist, INF, sizeof dist);
		dist[s] = 0; D.push(P(0, s));
		while (!D.empty())
		{
			P now = D.top(); D.pop();
			if (dist[now.second] < now.first) continue;
			int v = now.second;
			for (int i = 0; i<(int)G[v].size(); ++i)
			{
				edge &e = G[v][i];
				if (e.cap > 0 && dist[e.to] > dist[v] + e.cost + h[v] - h[e.to])
				{
					dist[e.to] = dist[v] + e.cost + h[v] - h[e.to];
					prevv[e.to] = v;
					preve[e.to] = i;
					D.push(P(dist[e.to], e.to));
				}
			}
		}
		if (dist[t] == INF) break;
		for (int i = 1; i <= n; ++i) h[i] += dist[i];
		int d = f;
		for (int v = t; v != s; v = prevv[v])
			d = min(d, G[prevv[v]][preve[v]].cap);
		f -= d; maxFlow += d;
		minCost += d * h[t];
		for (int v = t; v != s; v = prevv[v])
		{
			edge &e = G[prevv[v]][preve[v]];
			e.cap -= d;
			G[v][e.rev].cap += d;
		}
	}
}

int _tmain(int argc, _TCHAR* argv[])
{

	cout << "节点数为："; cin >> n;
	cout << "边数为："; cin >> m;
	cout << "源点编号为："; cin >> s;
	cout << "汇点编号为："; cin >> t;

	cout << "输入 " << m << " 条边的信息：" << endl;
	while (m--)
	{
		cout << "起点："; cin >> u;
		cout << "终点："; cin >> v;
		cout << "容量："; cin >> c;
		cout << "费用："; cin >> w;
		cout << "-----------------" << endl;
		addedge(u, v, c, w);
	}

	MCMF(s, t, INF);

	cout << "最大流为：" << maxFlow << endl;
	cout << "最小费用为" << minCost << endl;
	cout << endl;

	system("pause");
	return 0;
}

算法对比

名称	特点	不足
Bellman-Ford	可以解决负权边，但不允许有负环	每次循环值均对所有元素进行松弛判断，造成许多不必要的操作。
SPFA	进阶版的BF，使用队列进行优化，每次循环值选择当前节点相邻的若干节点进行松弛。在稀疏图上十分高效。	单路增广。SPFA需要维护较为复杂的标号和队列操作，同时为了修正标号，需要不止一次地访问某些节点，速度会比较慢。
改进的Dijkstra	速度普遍比SPFA要快。	无法直接处理负权边图，需要对算法进行改进。

补充

除了上述三种算法之外，还有诸如Dinic、ZKW等算法，不过个人没有研究，这里就不再赘述了。

参考文献

[1] 最小费用最大流(详解+模板)
[2] 数据结构与算法分析 - 网络流入门（Network Flow）
[3] 最小费用最大流问题
[4] 维基百科-最小费用最大流问题
[5]【最小费用最大流】知识点讲解
[6] P3381 【模板】最小费用最大流 题解