最短路问题 - 模板总结(Dijkstra + Bellman-Ford + SPFA + Floyd)

最短路问题 - 模板总结(Dijkstra + Bellman-ford + SPFA + Floyd)

最短路问题分类图：

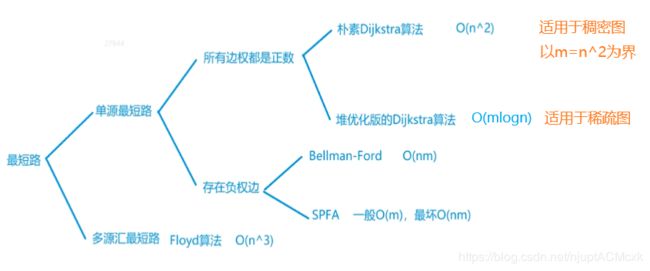
1、Dijkstra算法（正边权单源最短路问题）

1-1、朴素Dijkstra算法-O(n²)

给定一个n个点m条边的有向图，图中可能存在重边和自环，所有边权均为正值。

请你求出1号点到n号点的最短距离，如果无法从1号点走到n号点，则输出-1。

输入格式
第一行包含整数n和m。

接下来m行每行包含三个整数x，y，z，表示存在一条从点x到点y的有向边，边长为z。

输出格式
输出一个整数，表示1号点到n号点的最短距离。

如果路径不存在，则输出-1。

数据范围
1≤n≤500,
1≤m≤105,
图中涉及边长均不超过10000。

输入样例：
3 3
1 2 2
2 3 1
1 3 4
输出样例：
3

---

分析：

$本题m>n^2，用O(n^2)算法更优。$

$稠密图用邻接矩阵存储。注意到有重边，在读入的时候取重边中最小的权重即可。$

具体落实：

$$\begin{gathered} ①、整个点集分为两部分，一部分是到起点的最短距离已经确定，记为S_1。另一部分未确定，记为S_2。 \\ 首先初始化距离dis数组为+\infty ，起点所在位置dis[S]=0，就说将起点加入S_1。 \\ 再用起点去更新S_2中的点j到起点的最短距离dis[j]。 \\ 接下来的每次操作，都从S_2中选择一个到S_1距离最近的点t，再用点t去更新S_2中的点到起点的最短距离。 \end{gathered}$$

$②、以上操作重复n次，将n个点都加入到S_1中，此时的dis数组存储的就是到任意点到起点的最短距离。$
模板：

#include
#include
#include
#include

using namespace std;

const int N=510;

int n,m,g[N][N],dis[N];
bool st[N];

int dijkstra(int S)
{
    memset(dis,0x3f,sizeof dis);
    dis[S]=0;
    
    for(int i=0;i<n;i++)
    {
        int t=-1;
        for(int j=1;j<=n;j++)
            if(!st[j] && (t==-1 || dis[t]>dis[j]))
                t=j;
                
        st[t]=true;
        
        for(int j=1;j<=n;j++)
            dis[j]=min(dis[j],dis[t]+g[t][j]);
    }
    
    return dis[n]==0x3f3f3f3f ? -1 : dis[n];
    
}

int main()
{
    memset(g,0x3f,sizeof g);
    cin>>n>>m;
    for(int i=0;i<m;i++)
    {
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        g[a][b]=min(g[a][b],c);
    }
    
    cout<<dijkstra(1)<<endl;
    
    return 0;
}

---

1-2、堆优化的Dijkstra算法-O(mlogn)

给定一个n个点m条边的有向图，图中可能存在重边和自环，所有边权均为非负值。

请你求出1号点到n号点的最短距离，如果无法从1号点走到n号点，则输出-1。

输入格式
第一行包含整数n和m。

接下来m行每行包含三个整数x，y，z，表示存在一条从点x到点y的有向边，边长为z。

输出格式
输出一个整数，表示1号点到n号点的最短距离。

如果路径不存在，则输出-1。

数据范围
1≤n,m≤1.5×10⁵,
图中涉及边长均不小于0，且不超过10000。

输入样例：
3 3
1 2 2
2 3 1
1 3 4
输出样例：
3

---

分析：

$n<=10^5，此时O(n^2)效率明显低于O(mlo{g}_{2}n)，采用堆优化版的Dijkstra算法。$

$稀疏图，采用邻接表存储图。$

$$\begin{gathered} 通过分析朴素的Dijkstra算法，容易发现， \\ 我们每一趟都需要遍历点集中的所有点来寻找到当前到原点距离最近的点。 \\ 事实上，这个过程可以通过小根堆来维护。 \end{gathered}$$

$$\begin{gathered} 这样我们每次从小根堆中取出的就是S_2中到起点距离最近的点，再用该点更新S_2中与其相邻的点到起点的距离， \\ 并加入堆中。再重复操作即可。 \end{gathered}$$

代码：

#include
#include
#include
#include
#include

#define P pair

using namespace std;

const int N=1e6+10;

int n,m,e[N],w[N],ne[N],h[N],idx;
bool st[N];

void add(int a,int b,int c)
{
    e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}

int dijkstra()
{
    int dis[N];
    memset(dis,0x3f,sizeof dis);
    dis[1]=0;
    
    priority_queue<P,vector<P>,greater<P>> heap;
    heap.push({0,1});
    
    while(heap.size())
    {
        P t=heap.top();
        heap.pop();
        
        int id=t.second;
        if(st[id]) continue;
        st[id]=true;
        
        for(int i=h[id];~i;i=ne[i])
        {
            int j=e[i];
            if(dis[j]>dis[id]+w[i])
            {
                dis[j]=dis[id]+w[i];
                heap.push({dis[j],j});
            }
        }
    }
    
    return dis[n]==0x3f3f3f3f ? -1 : dis[n];
    
}


int main()
{
    memset(h,-1,sizeof h);
    scanf("%d%d",&n,&m);
    for(int i=0;i<m;i++)
    {
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        add(a,b,c);
    }
    
    cout<<dijkstra()<<endl;
    
    return 0;
}

---

2、Bellman-Ford算法(带负权且经过的边的数量有限制)-O(nm)

给定一个n个点m条边的有向图，图中可能存在重边和自环， 边权可能为负数。

请你求出从1号点到n号点的最多经过k条边的最短距离，如果无法从1号点走到n号点，输出impossible。

注意：图中可能 存在负权回路 。

输入格式
第一行包含三个整数n，m，k。

接下来m行，每行包含三个整数x，y，z，表示存在一条从点x到点y的有向边，边长为z。

输出格式
输出一个整数，表示从1号点到n号点的最多经过k条边的最短距离。

如果不存在满足条件的路径，则输出“impossible”。

数据范围
1≤n,k≤500,
1≤m≤10000,
任意边长的绝对值不超过10000。

输入样例：
3 3 1
1 2 1
2 3 1
1 3 3
输出样例：
3

---

分析：

$有负权回路，最短路未必存在(起点到终点的路径上未经过负权环，此时仍然是有最短路的)。$

$共迭代k次，每次遍历所有的边，更新所有点到起点的最短距离。$

代码：

#include
#include
#include
#include

using namespace std;

const int N=10010;

int n,m,k,backup[N];
struct Edge
{
    int u,v,w;  
}e[N];

int bellman_ford()
{
    int dis[N];
    memset(dis,0x3f,sizeof dis);
    dis[1]=0;
    
    for(int i=0;i<k;i++)
    {
        memcpy(backup,dis,sizeof dis);
        for(int j=1;j<=m;j++)
        {
            int a=e[j].u,b=e[j].v,w=e[j].w;
            dis[b]=min(dis[b],backup[a]+w);
        }
    }
    
    return dis[n]>0x3f3f3f3f/2 ? -1 : dis[n];
}

int main()
{
    cin>>n>>m>>k;
    for(int i=1;i<=m;i++) scanf("%d%d%d",&e[i].u,&e[i].v,&e[i].w);
    
    int t=bellman_ford();
    if(t==-1) puts("impossible");
    else cout<<t<<endl;
    
    return 0;
}

---

3、SPFA算法(带负权的最短路)-O(m)~O(nm)

3-1、SPFA求最短路

给定一个n个点m条边的有向图，图中可能存在重边和自环， 边权可能为负数。

请你求出1号点到n号点的最短距离，如果无法从1号点走到n号点，则输出impossible。

数据保证不存在负权回路。

输入格式
第一行包含整数n和m。

接下来m行每行包含三个整数x，y，z，表示存在一条从点x到点y的有向边，边长为z。

输出格式
输出一个整数，表示1号点到n号点的最短距离。

如果路径不存在，则输出”impossible”。

数据范围
1≤n,m≤10⁵
图中涉及边长绝对值均不超过10000。

输入样例：
3 3
1 2 5
2 3 -3
1 3 4
输出样例：
2

---

分析：

$$\begin{gathered} SPFA算法是Bellman-Ford算法的优化， \\ 我们发现BF算法每次迭代均要遍历所有的边，但事实上，并不是所有边均会被更新得更小。 \\ 转移方程：dis[b]=min(dis[b],dis[a]+w)，可见，只有当dis[a]减小，dis[w]才会变小。 \\ 因此，只有当某个点到起点的距离变小，经过该节点的其他点到起点的距离才可能变小。 \end{gathered}$$

$$\begin{gathered} 我们采用BFS的思想来对BF算法进行优化， \\ 用一个队列来存储到起点距离变短的点，每次出队后用该点更新与其相邻节点到起点的距离， \\ 再将更新过的到起点距离变短的点继续入队。 \end{gathered}$$

$$\begin{gathered} 需要注意，由于存在负权边，因此我们初始化的+\infty 可能会略微的减小。 \\ 因此我们认为若某点到起点的距离大于\frac{+\infty }{2}，则说明从起点无法到达该点。 \end{gathered}$$

代码：

#include
#include
#include
#include
#include

using namespace std;

const int N=100010;

int n,m,e[N],h[N],w[N],ne[N],idx;
bool st[N];

void add(int a,int b,int c)
{
    e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}

int spfa()
{
    int dis[N];
    memset(dis,0x3f,sizeof dis);
    dis[1]=0;
    
    queue<int> Q;
    Q.push(1);
    st[1]=true;
    
    while(Q.size())
    {
        int u=Q.front();
        Q.pop();
        st[u]=false;
        
        for(int i=h[u];~i;i=ne[i])
        {
            int j=e[i];
            if(dis[j]>dis[u]+w[i])
            {
                dis[j]=dis[u]+w[i];
                if(!st[j])
                {
                    st[j]=true;
                    Q.push(j);
                }
            }
        }
    }
    
    return dis[n];
}

int main()
{
    memset(h,-1,sizeof h);
    cin>>n>>m;
    for(int i=0;i<m;i++)
    {
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        add(a,b,c);
    }
    
    int t=spfa();
    if(t==0x3f3f3f3f) puts("impossible");
    else cout<<t<<endl;
    
    return 0;
}

---

3-2、SPFA判断负环

给定一个n个点m条边的有向图，图中可能存在重边和自环， 边权可能为负数。

请你判断图中是否存在负权回路。

输入格式
第一行包含整数n和m。

接下来m行每行包含三个整数x，y，z，表示存在一条从点x到点y的有向边，边长为z。

输出格式
如果图中存在负权回路，则输出“Yes”，否则输出“No”。

数据范围
1≤n≤2000,
1≤m≤10000,
图中涉及边长绝对值均不超过10000。

输入样例：
3 3
1 2 -1
2 3 4
3 1 -4
输出样例：
Yes

---

分析：

$与求最短路的思路类似，需额外增加数组cnt[x]，记录起点到x点经过的边数。$

$$\begin{gathered} 若cnt[x]>=n，表示从起点到x点经过了n条边，意味着经过了n+1个点，由抽屉原理，必然有某个点经过了2次。 \\ 这就说明了图中存在一个负环。 \end{gathered}$$

$$\begin{gathered} 与最短路不同的是，这次我们要先将所有点入队。 \\ 因为负环可能从某个起点出发未必能经过，需要将所有点都当作起点跑SPFA。 \end{gathered}$$

代码：

#include 
#include 
#include 
#include 

using namespace std;

const int N = 2010, M = 10010;

int n, m;
int h[N], w[M], e[M], ne[M], idx;
int dist[N], cnt[N];
bool st[N];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}

bool spfa()
{
    queue<int> q;

    for (int i = 1; i <= n; i ++ )
    {
        st[i] = true;
        q.push(i);
    }

    while (q.size())
    {
        int t = q.front();
        q.pop();

        st[t] = false;

        for (int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if (dist[j] > dist[t] + w[i])
            {
                dist[j] = dist[t] + w[i];
                cnt[j] = cnt[t] + 1;

                if (cnt[j] >= n) return true;
                if (!st[j])
                {
                    q.push(j);
                    st[j] = true;
                }
            }
        }
    }

    return false;
}

int main()
{
    scanf("%d%d", &n, &m);

    memset(h, -1, sizeof h);

    while (m -- )
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c);
    }

    if (spfa()) puts("Yes");
    else puts("No");

    return 0;
}

---

4、Floyd(多源最短路)-O(n³)

给定一个n个点m条边的有向图，图中可能存在重边和自环，边权可能为负数。

再给定k个询问，每个询问包含两个整数x和y，表示查询从点x到点y的最短距离，如果路径不存在，则输出“impossible”。

数据保证图中不存在负权回路。

输入格式
第一行包含三个整数n，m，k

接下来m行，每行包含三个整数x，y，z，表示存在一条从点x到点y的有向边，边长为z。

接下来k行，每行包含两个整数x，y，表示询问点x到点y的最短距离。

输出格式
共k行，每行输出一个整数，表示询问的结果，若询问两点间不存在路径，则输出“impossible”。

数据范围
1≤n≤200,
1≤k≤n2
1≤m≤20000,
图中涉及边长绝对值均不超过10000。

输入样例：
3 3 2
1 2 1
2 3 2
1 3 1
2 1
1 3
输出样例：
impossible
1

---

$思路十分简单，枚举中间点k，更新所有从i到j且经过k的路径的最短距离。$

$同样的，由于存在负权边，若距离仍大于\frac{+\infty }{2}，则认为两点之间不连通。$

代码：

#include
#include
#include
#include

#define inf 0x3f3f3f3f

using namespace std;

const int N=210;

int n,m,q,d[N][N];

void floyd()
{
    for(int k=1;k<=n;k++)
        for(int i=1;i<=n;i++)
            for(int j=1;j<=n;j++)
                d[i][j]=min(d[i][j],d[i][k]+d[k][j]);
}

int main()
{
    cin>>n>>m>>q;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            if(i==j) d[i][j]=0;
            else d[i][j]=inf;
            
    for(int i=0;i<m;i++)
    {
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        d[a][b]=min(d[a][b],c);
    }
    
    floyd();
    
    while(q--)
    {
        int a,b;
        scanf("%d%d",&a,&b);
        if(d[a][b]>inf/2) puts("impossible");
        else printf("%d\n",d[a][b]);
    }
    
    return 0;
}

---