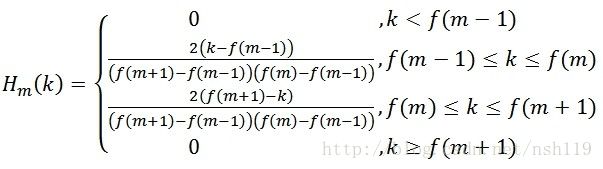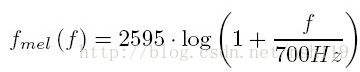语音识别-MFCC特征提取

本文是在上一篇文章（语音识别-预处理）的基础上进行的。

    梅尔频率倒谱系数（MFCC）：梅尔频率是基于人耳听觉特性提出来的， 它与Hz频率成非线性对应关系。梅尔频率倒谱系数(MFCC)则是利用它们之间的这种关系，计算得到的Hz频谱特征。主要用于语音数据特征提取和降低运算维度。

其主要过程为：

1. 离散傅里叶变换

    离散傅里叶变DFT的输入是一帧帧加窗后的信号x[n]…x[m]，输出则是包含N个频带的复数X[k]，表示原始信号中某一频率成分的幅度和相位。DFT的定义如下：

        

    计算DFT常用的一个算法是快速傅里叶变换（FFT），它非常高效但是一般要求N是2的幂。

2.Mel滤波器组（Mel刻度下的三角带通滤波器组）

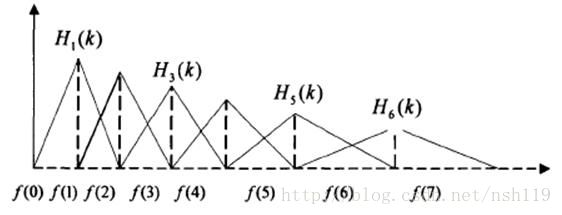
    Mel滤波器组一般是一组mel刻度的三角形滤波器组，1000Hz以下的10个滤波器线性相隔，1000Hz以上的剩余滤波器对数相隔。定义一个有M个滤波器的滤波器组，采用的滤波器为三角滤波器，中心频率为f(m)，m=1，2，…，M，M通常取22-26（滤波器的个数和临界带个数相近）。各f(m)之间的间隔随着m值的减小而缩小，随着m值的增大而增宽，如图：

    三角带通滤波器，可以对频谱进行平滑，并消除谐波的作用，突显原始声音的共振峰。因此一段声音的音调或音高，不会反应在MFCC参数内，也就是说以MFCC作为声学特征，并不会受到输入声音的音调不同而对识别结果有所影响。此外，还可以降低运算量。

    通过三角滤波器后，频率响应为：

其中 

3.对数

    在得到mel频谱后，计算每个滤波器组输出的对数能量。一般人对声音声压的反应呈对数关系，人对高声压的细微变化敏感度不如低声压。此外，使用对数可以降低提取的特征对输入声音能量变化的敏感度，因为声音与麦克风之间的距离是变化的，因而麦克风采集到的声音能量也是变化的。每个滤波器输出的对数能量为：

4.倒谱

    倒谱的定义可以看做是频谱对数的频谱，即将标准幅度谱的幅度值先取对数，然后形象化对数谱使其看起来像声音波形。倒谱这个单词cepstrum正是将单词spectrum（频谱）的前四个字母颠倒而来，频谱是将时域信号变换为频域信号，倒谱则是将频域信号又变换回时域信号；在波形上，倒谱与频谱有相似的波形，即如果频谱在低频处有个峰值，则倒谱在低倒谱系数上也有峰值，如果频谱在高频处有个峰值，则倒谱在高倒谱系数上也有峰值。所以如果是为了检测音元，可以用低倒谱系数；如果是检测音高，则可以用高倒谱系数。倒谱系数的优点是其不同系数的变化是不相关的，通常情况下，使用离散余弦变换来代替反傅里叶变换来获得倒谱，其公式如下：

5.能量与查分

 某一帧的能量定义为某一帧样本点的平方和，对于一个加窗信号x，其从样本点t1到样本点t2的能量为：

        

实际应用中也可以将上式取以10为底的对数值，再乘以10。若要加入其他声音特征如音高、过零率及共振峰等也可以在这一阶段加入。

        以上提取的特征每一帧单独考虑，是静态的，而实际声音是连续的，帧与帧之间是有联系的，因而需要增加特征来表示这种帧间的动态变化，这通常通过计算每一帧13个特征（12个倒谱特征加上1个能量）的一阶差分甚至二阶差分来实现。一个简单计算差分的方法就是计算当前帧前后各一帧的13个特征的差值：

        

        如果不考虑二阶差分，最终每一帧的MFCC特征为26维度：12维倒谱系数、12维倒谱系数差分、1维能量和1维能量差分。

上述就是语音信号在经过预处理后进行MFCC特征提取的具体过程。

附言

其中的Mel频率与Mel滤波器组的具体分析如下：

梅尔频率：模拟人耳对不同频率语音的感知。人类对不同频率语音有不同的感知能力：对1kHz以下，与频率成线性关系，对1kHz以上，与频率成对数关系。频率越高，感知能力就越差了， 梅尔频率具有这样的特性。Mel频率与Hz频率的转化关系为：

Mel滤波器组的具体设计的过程如下：

    假设语音信号的采样频率,帧长N=256，滤波器个数K=22

    由此可得语音信号的最大频率为：

    根据Mel频率与Hz频率的转化关系公式可以求得出最大的Mel频率为：

    由于在Mel刻度范围内，各个三角滤波器的中心频率是相等间隔的线性分布。由此，可以计算两个相邻三角滤波器的中心频率的间距为：

    因此，各三角形滤波器在mel刻度上的中心频率可以由Mel频率与线性频率的关系式求出。

    由上面的中心频率可以计算出对应的线性刻度上的频率。如下图所示：