全国新型肺炎累计感染数预测
全国新型肺炎累计感染数预测
摘要
春节无所事事,做了篇关于武汉肺炎的预测模型,预测标的是全国累计感染病例,模型采用2020-01-21到2020-01-29的数据作为训练集,利用皮尔生长曲线,结合贝叶斯估计,对当前的全国累计感染肺炎数据做出预测。结论:预测2020-01-30的全国累计感染新型肺炎总数为10459例;2020-02-11号预测感染人数达到了最大值,即预测当体全国累计感染人数为42526例;每日新增人数在2月3日达到了最大,即预测那一天新增4379例感染者,后期的新增感染病例逐步降低,直到为0。
1.1 累计感染者基本模型
病毒感染可看做是病毒这种生物繁衍的一种,描述生物繁衍的模型常用的有皮尔模型和Gompertz模型,这里假设真实感染者数量是一个皮尔过程,可以用一个生长曲线来描述,原因:
-
新型肺炎的初始阶段,感染人数少,但增长较快,此时由于对该病情的了解不深,预防措施较少,因此,一旦暴露在有病毒的环境下,
受感染的几率就较大,也就是此时的感染率最高。 -
后期人们逐步认识到病情的严重性,各种预防措施使得即使暴露在病毒的环境中,受感染的几率也低于初期,因为,中期传播感染率
较低,但是由于人口基数较大,因此,此时的感染量是最大的。 -
末期病毒得到控制或感染趋于饱和,此时感染绝对数量达到最大,但几乎不会再产生新的感染病例,随着治疗出院人口的增加,净感染人数为负的状态。
假设 y t y_t yt表示当日的总累计感染人数,该变量服从如下过程:
d y d t = γ ⋅ y ( 1 − y k ) (1.1) {dy\over dt}=\gamma·y(1-{y\over k})\tag {1.1} dtdy=γ⋅y(1−ky)(1.1)
其中 γ \gamma γ表示增长率, k k k表示在给定的资源禀赋下,生物群体能达到的最大量,也称为承载力, t t t表示时间。上述方程式描述生物群体单位时间增加量的建模过程,即可以理解为单位时间内的新增病例等于群体按一定增长率 γ \gamma γ增长,而后又受制于资源的约束,越接近于群体最大上限,
增加量越小,用 y k {y\over k} ky表示接近群体潜在最大上限,增长量跟这个指标呈反比,这里假设线性关系,所以该增量分解了两个部分,一个部分是自然增长,另一个部分是资源约束下,导致一部分增长无效,即需要扣除的增长部分。
方程(1)给出y的初始值可以求出微分方程的解:
y t = k 1 + ( y 0 k − 1 ) e − γ ⋅ t (1.2) y_t =\frac {k}{1+({y_0\over k}-1)e^{-\gamma·t}} \tag{1.2} yt=1+(ky0−1)e−γ⋅tk(1.2)
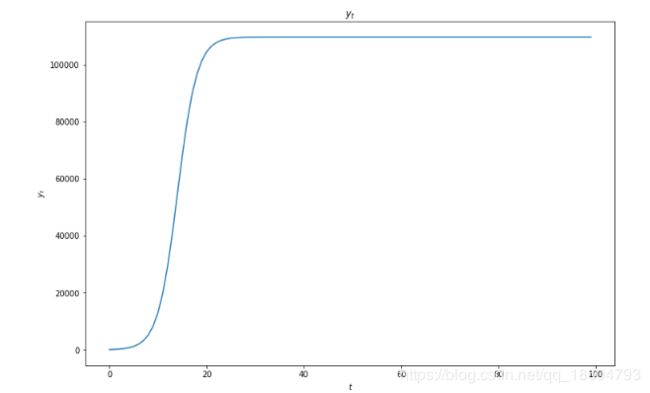
其中 y 0 y_0 y0表示 y y y的初始值。生长曲线大致的样子如下:
1.2 扩展模型
由于现实情况比较复杂,受诸多因素的影响,新型肺炎的传播可以从两个角度扩散,我称之为“宽度”和“深度”,宽度可以理解为具有传播能力的个人组成的集体,这个集体平均每日新增密切接触者人数,深度可以理解为每百位密切接触者被感染者比例,肺炎发展的不同时期所采取的措施,通过影响深度或者宽度,进而来影响最终疾病的传播速度和数量,比如通过戴口罩可以降低被感染几率,通过躲在屋里不出来,可以降低新增密切接触者人数,这些举措都在影响着方程中的参数 γ \gamma γ和 k k k,因此,这里我们把这两个参数内生化,把他们看做是随着某些因素在变化的过程,这些因素比如每百人开口罩人数比例,平均每人在公共场所的时间,交通人流等等,由于数据不可得,把 γ \gamma γ看做是时间 t t t的函数,而承载力k的放松方式我们采用另外一种方式,这里暂且不讨论;
希望扩展模型后,模型能体现出如下特点:
- 随着时间的增加,新型肺炎的增长率是在下降的,如图2所示;
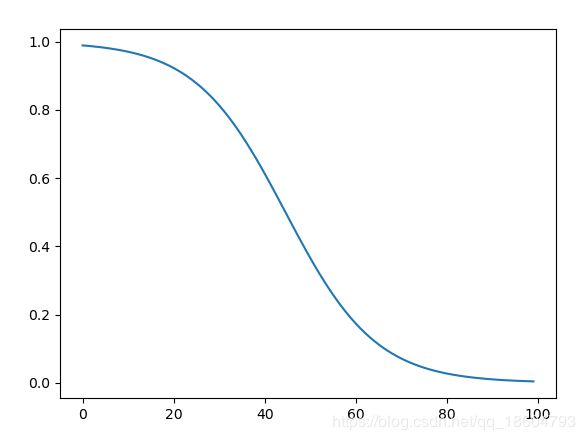
- 随着时间的增加,承载力是在下降的,如果是自然状态下,假设病毒来了,人们没有应对的行为,任凭病毒肆意自然传播,那么承载力应该是固定不变的,比如14亿人口,最终可能会感染到一定比例后,达到最大上限;由于人们的干扰行为导致承载力也是在下降的,因此,这里希望模型具有如下特点;如图所示承载力随时间下降,而累积被感染人数随时间递增,最终二者交汇在一起,感染人数达到上限,病毒传播也告一段落;

- 利用专家或者现有的研究成果修正模型参数。
1.2.1 拓展后的模型形式
为了实现上述对模型的要求,我们对模型做了如下拓展:
{ y t = k ( c h a n g e _ p o i n t , γ ) 1 + ( y 0 k − 1 ) e − γ ⋅ t + ϵ t γ ( t ) = 1 1 + e β ⋅ t + α (1.3) \left \{ \begin{array}{c} y_t =\frac {k(change\_point,\gamma)}{1+({y_0\over k}-1)e^{-\gamma·t}} + \epsilon_t \\ \gamma(t)={1\over{1+ e^{\beta·t+\alpha}}} \tag{1.3} \end{array} \right. {yt=1+(ky0−1)e−γ⋅tk(change_point,γ)+ϵtγ(t)=1+eβ⋅t+α1(1.3)
公式(1.3)式相对公式(1.1)有三处改变:
- 增加了随机干扰项 ϵ t \epsilon_t ϵt,通常假设 ϵ t ∼ i i d N ( 0 , σ 2 ) \epsilon_t\sim iidN(0,\sigma^2) ϵt∼iidN(0,σ2)
- 把 γ \gamma γ与时间 t t t的关系用一个logistic函数来表示,这是因为我们希望 γ \gamma γ是随时间衰减,且希望在不同时间段具有不同的衰减强度,该函数可以实现我的这种想法;
- 把 k k k看做是一个变量,引入一个叫做 c h a n g e _ p o i n t change\_point change_point的变量,将承载力 k k k看做是增长率 γ \gamma γ和 c h a n g e _ p o i n t change\_point change_point的函数。先给出change_point(拐点)的定义,拐点就是增长量出现下降的点,也是上述模型中,一阶导数达到最大的点,总之,看到拐点了,就认为每日新增感染者开始逐步减小了。具体可参考文献【1】。当已知增长率和拐点,则可以推出承载力 k k k,已知承载力 k k k,则可以推出拐点,因此,这里我们把承载力 k k k看做是拐点。
到此为止,仍需要解决的问题有:
- 怎么利用现有的武汉肺炎研究的先验信息问题;
- 参数估计问题。
1.2.2 模型的进一步拓展——贝叶斯方法
首先,先探讨方程(1.3)的参数估计问题,方程含有 k k k, γ , β , α , τ \gamma,\beta,\alpha,\tau γ,β,α,τ 5个参数,且方程式非线性方程,相对来讲这个非线性方程比较简单,可以在假设 β , α \beta,\alpha β,α是给定常数的情况下,把非线性方程转化为线性方程,即转化为可以用最小二乘法或最大似然法求解其他参数,然后将上述解作为迭代法的初始值,用迭代法就可以求出所有参数的值,但是,这往往需要有较多的观测值,实际情况,我们从国家卫健委公布的数据,长度不过10天左右,那么有仅有的几个数据,来估计模型的参数,随机性太大,得出的参数太不靠靠,另外,采用这种方式,我们就很难将现有的研究成果综合到模型中去了,因此,这里抛弃这种解题思路,转为利用贝叶斯法。
所谓的贝叶斯法,这里是把模型中所涉及到的参数都给随机化,都把他们看做是服从某种分布的随机变量,或者某些随机变量的函数。这里大致把思路说下,细节不详讲,假设每天累计病患数服从某个分布,每日政府官网报告的数据,就是这个分布的一个采样,该分布函数记作 p ( 每 天 累 计 病 患 数 ) p(每天累计病患数) p(每天累计病患数),每天的观测值,是在一定的参数条件下的观测结果(虽然参数是多少我们不知道,但他们确实以一定形式存在),即
p ( 每 天 累 计 病 患 数 ∣ 参 数 空 间 ) = p ( 参 数 空 间 ∣ 每 天 累 计 病 患 数 ) ⋅ p ( 每 天 累 计 病 患 数 ) p ( 参 数 空 间 ) p(每天累计病患数|参数空间)={p(参数空间|每天累计病患数)·p(每天累计病患数)\over p(参数空间)} p(每天累计病患数∣参数空间)=p(参数空间)p(参数空间∣每天累计病患数)⋅p(每天累计病患数)
其中 p ( 每 天 累 计 病 患 数 ∣ 参 数 空 间 ) p(每天累计病患数∣参数空间) p(每天累计病患数∣参数空间)与 p ( 参 数 空 间 ∣ 每 天 累 计 病 患 数 ) ⋅ p ( 每 天 累 计 病 患 数 ) p(参数空间|每天累计病患数)·p(每天累计病患数) p(参数空间∣每天累计病患数)⋅p(每天累计病患数)有相同的单调性,当用前者构建似然函数时,就可以用后者代替子似然函数中的位置,进而求出参数的后验分布。
那么接下来将解决第一个问题,即我们把上面涉及到的5个参数,都把它们看做是服从某种分布的随机变量,具体分布函数形式怎样,我们将在下面的章节来分别构建,这就是参数的先验分布问题。
1.3 参变量的先验分布形式
1.3.1 承载力 k k k(change_point)的先验分布
从数学上知道拐点和承载力可以相互转换,那我们为什么要用拐点而不用承载力呢,这是因为关于承载力很难找到相关的论断(除去一些预测模型做的预测),而大家似乎对拐点有比较多的意见,这为搜集主观信息提供了便利的条件。从当前的新闻信息我梳理了如下几条先验证信息:
- 国家对武汉新型肺炎的管控措施强度时间点————武汉严格出入严格管控:1月21日
- 新型肺炎的潜伏期时间长度;最长14天,主要集中在前3-7天
- 专家给出的拐点出现的位置为正月15号左右。
在1月21号之前,还存在如下问题:
- 武汉公布的数据失真,政府还有点遮遮掩掩的态度;
- 1月21号前后是春运高峰期;
- 民众普遍感知较弱,以我为例,只觉得当时还很遥远;
由于重视程度不够,又赶上春运,加上潜伏期两周,所以,即使后来做了管控,依旧会出现一波病毒爆发增长期,时间最长两周左右,这两周内,将最大出现增长率的最大峰值,同时,由于严控的实施,政策效应其效果要等到前期潜伏病患告一段落,结合着专家观点,预计自1月21号其,向后推两周,也就是2月4号,将很可能达到增长的** 拐点**,我们这里假定2月3号,2月4号,2月5号将出现增长量的拐点,称这些天为重点关注天,把拐点出现在哪一天看做是一个概率分布,我们给出如下的先验分布:
拐点的先验分布:假设分段均匀分布,且根据先验信息,推断拐点出现在大概率出现在2月3号-2月5号之间,出现在这区间之前的概率和这区间之后的概率假设相等,具体是多少呢,把给定的时间划分为3部分,第一部分就是重点关注天之前的部分,第二部分就是重点关注天,第三部分就是重点关注天之后的部分,每一部分的概率相等,即为1/3,而每一部分又包含了若干天,每一部分的每一天假设概率也相等,比如重点关注天为2月3号,2月4号,2月5号,我们假设这三天等概率,而这一部分的总概率占1/3,则每一天占1/3*1/3=0.1111。
拐点的分布是一个分段函数,我将会引入另一个随机变量来表示拐点,即把拐点看做:
{ c h a n g e _ p o i n t = f ( ρ ) ρ ∼ U ( 0 , 100 ) (1.4) \left \{ \begin{array}{c} change\_point=f(\rho) \\ \rho\sim U(0,100) \tag{1.4} \end{array} \right. {change_point=f(ρ)ρ∼U(0,100)(1.4)
下面是利用Buffon投针原理,用 ρ \rho ρ 实现 c h a n g e _ p o i n t change\_point change_point的代码:
#!/usr/bin/env python
# coding: utf-8
import pymc as pm
import pandas as pd
import numpy as np
import matplotlib as mpl
# mpl.use('agg')
import matplotlib.pyplot as plt
import matplotlib.patches as mpatches
import seaborn as sns # box -plot
from pathlib import Path
import pdb
import pickle
p = Path().resolve()
import warnings
warnings.filterwarnings('ignore')
print("this path:",p)
# 初始化,给出all_range和all_labels
range1 = np.arange(0,100,(100-0)/3).tolist()
range1.append(100)
# 这里可以通过设置不同的划分区间,来控制转变点的先验证分布
print(range1)
all_range = []
all_labels = []
range_num = {0:12,1:3,2:85}
labels = {0:[1,12],1:[13,15],2:[16,100]}
for i in range(len(range1)-1):
start,end = [range1[i],range1[i+1]]
sub_range_num = range_num[i]
sub_range = np.arange(start,end,(end-start)/sub_range_num).tolist()
sub_range.append(end)
all_range.extend(sub_range)
all_labels.extend(range(labels[i][0],labels[i][1]+1))
# 第一步,定义拐点:change_point
rho = pm.Uniform("rho", lower=0, upper=100)
@pm.deterministic
def change_point(rho=rho):
u= pd.cut([rho],np.unique(all_range),labels=all_labels)[0]
return int(u)
1.3.2 增长率 γ \gamma γ的先验分布
从公式(1.3)中我们假设 γ \gamma γ是 α , β \alpha,\beta α,β 的函数,只需构建 α , β \alpha,\beta α,β的先验分布,就可以得到 γ \gamma γ的先验分布,我们假设 γ \gamma γ是一个两参变量的logistic函数,那么且限定了它的承载力,即最大值为1,最小值0,也就是说我们的 γ \gamma γ取值在(0,1)之间,首先来看这个取值范围是否合理, γ \gamma γ表示增长率,现有的数据表示1个人平均感染2-4个人,这个是较高的估计,而保守估计是在1-2个人之间,然后,考虑到发病率和发病时间,这些人并不是同一天一起发病,而是一段时间逐步发病,我们前面有潜伏期和发病期的时间,潜伏期最大不超过14天,而一般在3-7日出现感染症状,这样来看,假设平均感染率为7天,那么其实平均到每一天的感染人数不足一个人,因此,从整个感染群体的增长来看,增长率小于1是合理的,并且我们预测的是新增感染数量,而不是治愈数量,因此,不低于0也合理;
选择logistic函数还有另一个好处是,可以通过参变量 α , β \alpha,\beta α,β 来得到不同单调性,不同增长率的函数,这里我们假设 α , β \alpha,\beta α,β的先验分布为分布,初始值为接近于0的常数:
{ γ ( t ) = 1 1 + e β ⋅ t + α α ∼ N ( 0 , 0.001 ) β ∼ N ( 0.001 , 0.001 ) (1.5) \left \{ \begin{array}{c} \gamma(t)={1\over{1+ e^{\beta·t+\alpha}}} \\ \alpha\sim N(0,0.001) \\ \beta\sim N(0.001,0.001) \tag{1.5} \end{array} \right. ⎩⎨⎧γ(t)=1+eβ⋅t+α1α∼N(0,0.001)β∼N(0.001,0.001)(1.5)
# 第二步,定义gamma
beta = pm.Normal("beta",0.001,0.001,value=0.1)
alpha = pm.Normal("alpha",0,0.001,value=0.0)
# 第三步,定义似然函数的标准差参数先验分布
@pm.deterministic
def gamma(t=t,alpha=alpha,beta=beta):
return 1.0 / (1.0 + np.exp(beta*t*0.1+alpha))
1.3.3 增长率 ϵ \epsilon ϵ的先验分布
ϵ \epsilon ϵ是随机干扰项,一般假设独立同分布,且0均值,这里我们把方差作为一个参数,这个参数的分布是(0,100)上的均匀分布;即
{ ϵ ∼ N ( 0 , 1 τ ) τ ∼ U ( 0 , 1 ) (1.6) \left \{ \begin{array}{c} \epsilon\sim N(0,{1\over{\tau}}) \\ \tau\sim U(0,1) \\ \tag{1.6} \end{array} \right. {ϵ∼N(0,τ1)τ∼U(0,1)(1.6)
以下是代码实现:
std = pm.Uniform("std",0,100,trace=False)
@pm.deterministic
def prec(U=std):
return 1.0/U**2
1.3.4 观测值的先验分布(似然函数)
我们假设观测值是正太分布,其均值就是我们建模给出的 y t y_t yt,其方差就是我们给定的随机干扰项的方程,即:
o b s ∼ N ( y t , 1 τ ) (1.7) obs\sim N(y_t,{1\over{\tau}}) \tag{1.7} obs∼N(yt,τ1)(1.7)
下面是实现的似然函数代码:
# 依赖的函数
def infections(gamma, change_point, y0, t):
"""
求生物群体大小
"""
all_y = [y0]
all_k = [y0 * (1 + np.exp(change_point * gamma[0]*1.0**0))]
all_delta_y = [y0]
last_y = y0
for i in t[1:]:
# 最大承载力不能低于前一期的生物总数
new_k = y0 * (1 + np.exp(change_point * gamma[i]*1.0**i))
k = max(new_k, all_y[i - 1])
y_i = k / (1 + (k/y0-1)*np.exp(-gamma[i]*i*1.0**i))
delta_y = max(y_i - all_y[i - 1], 0)
last_y = last_y + delta_y
if k < last_y:
k = last_y
all_delta_y.append(delta_y)
all_y.append(last_y)
all_k.append(k)
return np.cumsum(all_delta_y), all_k
def gamma_f(t, alpha, beta):
"用logistic函数来表示增长率的变化过程"
return 1.0 / (1.0 + np.exp(beta*t+alpha))
t = range(0,8)
date = pd.date_range(start='21/1/2020', periods=100)
result = pd.read_excel("确诊病例数据.xlsx")
Y = result["累计"].values[-8:]
y0=Y[0]
def f(gamma=gamma, change_point=change_point, y0=y0,t=t):
y, _ = infections(gamma=gamma, change_point=change_point, y0=y0,t=t)
return y
mean = pm.Lambda("mean",f)
# 第四步,给定观测值模型,似然函数
obs = pm.Normal("obs",mean,prec,value=Y,observed=True)
到此,我们完成了所有参变量的随机化,并给出了先验分布,下面解决第二个问题,估计参数问题。
1.3.5 参数估计
由于分布太复杂,我们用MCMC方法来求参数的后验分布。这里用2020-01-21到2020-01-28日全国累计被感染新型肺炎的总数作为观测数据,数据来源:国家卫健委http://www.nhc.gov.cn/
| 日期 | 全国累计感染总数(例) |
|---|---|
| 2020-01-21 | 440 |
| 2020-01-22 | 571 |
| 2020-01-23 | 830 |
| 2020-01-24 | 1287 |
| 2020-01-25 | 1975 |
| 2020-01-26 | 2744 |
| 2020-01-27 | 4515 |
| 2020-01-28 | 5974 |
| 2020-01-29 | 7711 |
其中21-28日作为样本内拟合参数的数据,29日作为样本外检验的数据。拟合模型的代码如下:
# 第五步,MCMC求后验分布
model = [obs,mean,prec,gamma,change_point,beta,alpha,rho]
mcmc = pm.MCMC(model)
mcmc.sample(100000,80000)
print("done!")
2.1 模型结果分析
2.1.1 拐点的后验分布
结论: 通过上述的模型拟合,我们来看下change_point的后验分布,在构造拐点的先验分布时,我们假定它是服从均匀分布的,只是这个均匀分布是个分段函数。下面给出了先验分布和后验分布的对比图,从图中可以看出(上面是先验分布,下面是后验分布),经过实际数据的“修正”,有些日期是拐点的概率为0,而有日期(我们假设的重点关注天)是拐点的概率变大了,说明实际数据更加支持了我们的主观猜测。
从数据来看,2月3日 出现拐点的概率最大,概率值为25.86%,2月2日-2月5日出现拐点的总概率为80%,说明拐点大概率在这个时间区间出现,而我们在前期,根据推测大致给出的时间是2月3日到2月5日,时间区间大致吻合。
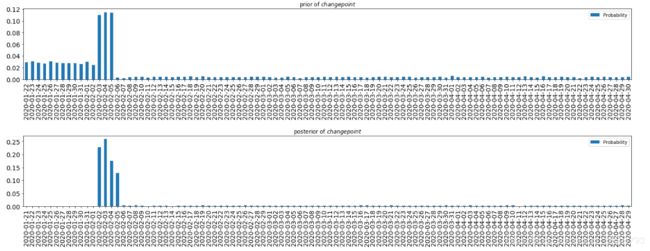
下面给出是拐点概率前10个最大值:
| 日期 | 是拐点的概率 (%) |
|---|---|
| 2月3日 | 25.86 |
| 2月2日 | 22.76 |
| 2月4日 | 17.56 |
| 2月5日 | 12.87 |
| 2月6日 | 0.445 |
| 3月16日 | 0.40 |
| 2月8日 | 0.38 |
| 4月28日 | 0.37 |
| 2月26日 | 0.35 |
| 2月19日 | 0.34 |
| 2月2日 | 22.76 |
| 2月2日 | 22.76 |
# 拐点的先验分布:利用蒙特卡洛法,从自己定义的分段概率分布中抽样10000次,统计各个值出现的频率
# 理论上出现13,14,15的概率为1/9=0.11111
all_test_result = []
# 蒙特卡洛模拟,生成1万次随机
for i in range(10000):
rho.random()
all_test_result.append(change_point.value)
test = pd.Series(all_test_result)
prior_distribution = test.value_counts()/len(test)
prior_distribution.index = [(date[0]+pd.Timedelta(days=i)).strftime("%Y-%m-%d") for i in prior_distribution.index]
prior_distribution.sort_index(inplace=True)
plt.subplot(211)
prior_distribution.plot(kind='bar',rot='90',figsize=(24,8),title='prior of $change point$',grid=False,fontsize=14,label="Probability")
plt.legend(loc='best')
# 拐点的后验分布
change_point_samples = mcmc.trace("change_point")[:]
posterior = pd.Series(change_point_samples)
frequence = posterior.value_counts()/len(posterior)
frequence.index = [date[0]+pd.Timedelta(days=i) for i in frequence.index]
frequence = frequence.reindex(date, fill_value=0)
frequence.index = [str(i) for i in frequence.index.date]
frequence.sort_index(inplace=True)
plt.subplot(212)
frequence.plot(kind='bar',rot='90',figsize=(24,8),title='posterior of $change point$',grid=False,fontsize=14,label="Probability")
plt.legend(loc='best')
plt.subplots_adjust(hspace=0.8)
plt.show()
print("拐点出现位置的概率分布top10:\n{}".format(frequence.sort_values(ascending=False).head(10)))
2.2.2 增长率 γ \gamma γ的后验分布
增长率 γ \gamma γ是 α \alpha α和 β \beta β的非线性函数,我们假设 α \alpha α和 β \beta β是正态的,具体 γ \gamma γ的分布是什么分布不清楚,我们只能抽样,不清楚他的分布函数的具体形态,由于增长率 γ \gamma γ依赖于两个参变量,先看这两个参变量的分布.。
γ \gamma γ的后验分布:
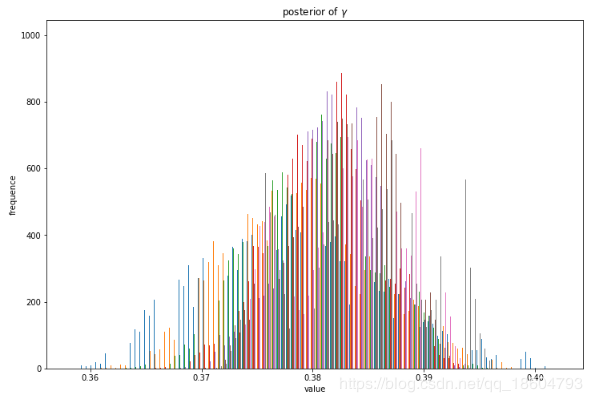
α 的 后 验 分 布 : \alpha的后验分布: α的后验分布:
β 的 后 验 分 布 : \beta的后验分布: β的后验分布:
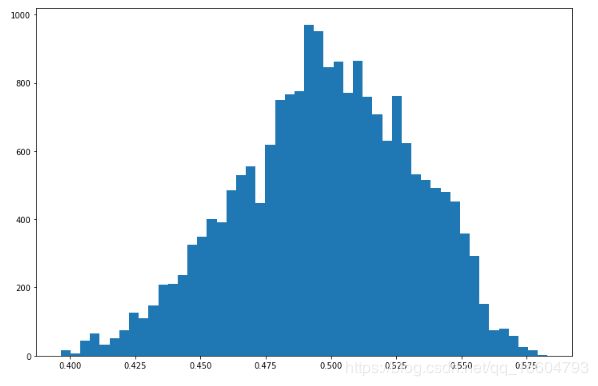
2.2.3 ρ \rho ρ的后验分布
在先验分布中,我们假设 ρ \rho ρ是[0,100]上的均匀分布,我们来看下它的后验分布变成什么样子。

2.3 样本外预测——未来的累计感染肺炎数量预测
有了上述模型的参数估计,下面来预测全国肺炎感染累计总数量,一次完整的时间序列预测,需要知道 ρ \rho ρ的一个标量值、 β \beta β的一个标量值、 α \alpha α的一个标量值,和t的一个时间序列值,上述采样,我们已经实现了这些参数的采样序列,那么就可以根据这些参数来做预测了。
下面定义预测模型,由于参数是采样得到,因此,要遍历这些采样得到的参数,每一组参数都会产生一组预测值。先把预测值保存下来,预测模型定义如下:
def forecast(t, change_point_samples, alpha_samples, beta_samples, y0=440):
all_forecast = []
all_max_value = []
for i in range(len(change_point_samples)):
gamma = gamma_f(t, alpha_samples[i], beta_samples[i])
change_point = change_point_samples[i]
forecast,max_value = infections(gamma=gamma, change_point=change_point, y0=y0, t=t)
all_max_value.append(max_value)
all_forecast.append(forecast)
return all_forecast,all_max_value
forecast_date_range = range(0,100)
下面将调用模型,预测预测2020年1月21号-2020年4月29号的数据,其中1月21号-1月28号是样本内数据,参与了模型参数的拟合,all_forecast表示所有参数的预测值集合,all_forecast_max_value承载力预测集合:
all_forecast,all_forecast_max_value = forecast(t=forecast_date_range,change_point_samples=change_point_samples,alpha_samples=alpha_samples,beta_samples=beta_samples,y0=440)
2.2.1 预测结果分析
2.2.1.1 每天全国累计感染者的预测值
由于我们进行了20000次采样,也就是说我们有2万组模型参数,只是有些参数出现的概率高有些参数出现的概率低,首先来看下预测矩阵的大小,是一个20000*100的矩阵,因为我们从1/21日开始(包含)向外预测,共预测100步,所以时间序列长度为100,而我们的采样为2万次,所以有2万个这种时间序列,如下图:

下面将进行每个日期预测值分布进行统计,由于皮尔模型对超参敏感,如果按照估计出来的超参的分布,进行采样,然后再统计预测值的分布是有很大问题的,举例说明一下,如果参数值取两个值比如0和1,该参数的后验分布是假设取到0的概率为80%,取到1的概率为20%,假设取到0时,预测值为2,而取到1时,预测值为2000000,如果真实参数值为0,即此时的预测值0,那么显然我们不能用采样出来的参数对应的预测值做均值来作为模型最终预测值,因为我们求均值时,里面混入了2000000这个很大的值,会把我们的预测值偏向于这个小概率参数的预测。
所以,我们要先对参数做一遍过滤,过滤的方法就是样本内的拟合度和样本外的预测精度,当参数所对应的的模型对样本内和样本外都有一定的预测精度,我们才把这个参数作为备选,这里我给的样本内时间点为1月26日,1月27日,1月28日,样本外的测试集我给的是1月29日,根据对这几天的预测综合误差,选出有效参数,再统计这些有效参数对应的预测值。这里我选择模型的原则是综合误差用mape定义,要求综合误差在2.5%以内;
date = pd.date_range(start='21/1/2020', periods=100)
result = pd.read_excel("确诊病例数据.xlsx")
obs_value = result["累计"].values[-9:]
# 测试集的误差权重较大,赋值为70%的权重,样本内的误差占比为30%
pd_forecast["mape"] = (0.7*abs(pd_forecast[[date[8]]]/obs_value[-1]-1).values + 0.1*abs(pd_forecast[[date[7]]]/obs_value[-2]-1).values + 0.1*abs(pd_forecast[[date[6]]]/obs_value[-3]-1).values+ 0.1*abs(pd_forecast[[date[5]]]/obs_value[-4]-1).values)
# pd_forecast.head(10)
sub_forecast = pd_forecast.loc[pd_forecast["mape"]<0.025]
# 通过选择
print("选择结果:",sub_forecast.shape)
sub_forecast = sub_forecast.T
sub_forecast = sub_forecast.drop(['mape'], axis=0)
sub_forecast.head(5)
为了给出每日累计感染者预测总数量,这里用所有参数预测的中位数作为预测值,命名为total number,每日增长量命名为growth,从预测数据来看2020-02-11号预测感染人数达到了最大值,即全国累计感染人数为42526例,后续就不在增加了。而每日新增人数在2月3日达到了最大,即预测那一天新增4379例感染者。下图全国累计的感染数预测,和增量预测。

每日的预测值如下:

2.2.1.2 每天全国累计感染者的预测值预测区间
这里没有给出置信区间,因为每一天的预测中,均含有异常值,有时异常值比例很高,会导致置信区间变形,需要去除异常值,去除异常值后,在给出置信区间,由于时间有限,这个工作就不做了,直接给出了剔除异常值后的所有预测值构成的预测区间。
# 求每天的预测分布
series_forecast = pd.DataFrame(sub_forecast.values.flatten(),index=np.array([[i.strftime("%Y-%m-%d")]*sub_forecast.shape[1] for i in sub_forecast.index]).flatten()).reset_index()
series_forecast.rename(columns={0:"forecast","index":"date"},inplace=True)
series_forecast
plt.close("all")
plt.figure(2211)
forecast_set = series_forecast.iloc[0:22*sub_forecast.shape[1],:].boxplot(column="forecast", by="date",figsize=(12,8),showfliers = False,showmeans=False, patch_artist=True,meanline=True,return_type='dict')
plt.xticks(rotation=45,fontsize=15)
forecast_medians = [i.get_ydata()[0]for i in forecast_set["forecast"]["medians"]] # 与自己求的mid值是一样的
# plt.plot(forecast_medians[0:21],'-or')
plt.show()
3.1 模型总结
1.模型完成于2020年1月28日,编辑工作完成与2020年1月29日,所以排版比较丑陋,模型假设受感染人数符合皮尔生长曲线特征,因此用皮尔曲线进行预测,在建模时,将增长率和承载力看做随时间变化的过程,这是考虑到随着实际情况,随着人们的干预,受感染过程并非一个自然增长,而是受控增长,这也是很多不了解国内情况的一批专家所忽略的,这也是我为什么要做这个预测的原因。
2.因为国内正值春节,春节的客流量预计未来几天会逐步增加,这个对模型的潜在影响并没有体现出来,可能会导致模型预测不准的以一个原因。
3.模型考虑了专家的意见,在针对拐点先验分布的假设上,综合的专家的意见,以及大致的病毒传播时间,给出了一个不是很严格的推理,并没有做严格的论证,还是有带改进的地方。
4.最后想要说的是,要坚定信心,不要做一个无知无畏的人,也不要如惊弓之鸟,具体怎么做呢,。。。,活一天赚一天吧。
模拟拟合的全部代码
后期其他代码将上传到githup
# 初始化,给出all_range和all_labels
range1 = np.arange(0,100,(100-0)/3).tolist()
range1.append(100)
# 这里可以通过设置不同的划分区间,来控制转变点的先验证分布
print(range1)
all_range = []
all_labels = []
range_num = {0:12,1:3,2:85}
labels = {0:[1,12],1:[13,15],2:[16,100]}
for i in range(len(range1)-1):
start,end = [range1[i],range1[i+1]]
sub_range_num = range_num[i]
sub_range = np.arange(start,end,(end-start)/sub_range_num).tolist()
sub_range.append(end)
all_range.extend(sub_range)
all_labels.extend(range(labels[i][0],labels[i][1]+1))
# 第一步,定义拐点:change_point
rho = pm.Uniform("rho", lower=0, upper=100)
@pm.deterministic
def change_point(rho=rho):
u= pd.cut([rho],np.unique(all_range),labels=all_labels)[0]
return int(u)
# 第二步,定义gamma
beta = pm.Normal("beta",0.001,0.001,value=0.1)
alpha = pm.Normal("alpha",0,0.001,value=0.0)
# 第三步,定义似然函数的标准差参数先验分布
@pm.deterministic
def gamma(t=t,alpha=alpha,beta=beta):
return 1.0 / (1.0 + np.exp(beta*t*0.1+alpha))
std = pm.Uniform("std",0,100,trace=False)
@pm.deterministic
def prec(U=std):
return 1.0/U**2
# 第四步,定义似然函数的均值先验分布
t = range(0,8)
date = pd.date_range(start='21/1/2020', periods=100)
result = pd.read_excel("确诊病例数据.xlsx")
Y = result["累计"].values[-8:]
y0=Y[0]
def f(gamma=gamma, change_point=change_point, y0=y0,t=t):
y, _ = infections(gamma=gamma, change_point=change_point, y0=y0,t=t)
return y
mean = pm.Lambda("mean",f)
# 第四步,给定观测值模型,似然函数
obs = pm.Normal("obs",mean,prec,value=Y,observed=True)
model = [obs,mean,prec,gamma,change_point,beta,alpha,rho]
# 第五步,MCMC求后验分布
mcmc = pm.MCMC(model)
mcmc.sample(100000,80000)
print("done!")
参考文献:
[1]: Cameron Davidson-Pilon,贝叶斯方法 概率编程与贝叶斯推断[M],…
[2]: 魏宗舒等,概率论与数理统计教程[M],…
[3]: 皮尔曲线模型的推广及其应用,https://wenku.baidu.com/view/8b3362afd1f34693daef3ee6.html
[4]: Logistic曲线与Gompertz曲线的比较研究,https://www.docin.com/p-944041461.html