强化学习基础——形象化解释值函数含义以及期望的意义

1.值函数定义

1.1 V函数

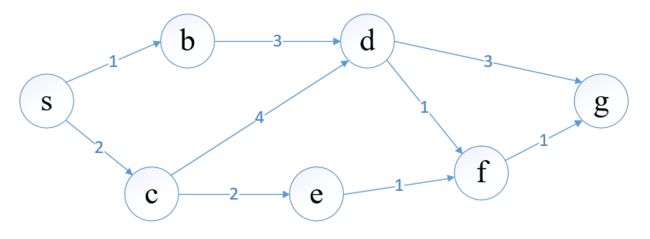
我们先看一下经典的最短路问题，假设我们要求出起点s到终点g的最短路

我们定义$V^{\ast }(s)$为$s$到终点$g$的最短路，$V^{\ast }(f)$ 为$f$到终点$g$的最短路，以此类推，为了求出这个最短路，我们从终点开始算起：
$$\begin{array}{rl}{V}^{\ast }(g)& =0\\ V^{\ast }(f)& =1+V^{\ast }(g)=1\\ V^{\ast }(d)& =min\{3+V^{\ast }(g),1+V^{\ast }(f)\}\end{array}$$

对终点$g$来说，自己到自己的最短路为0。

对顶点$f$来说，只有它自己和终点$g$有路径，故顶点$f$到$g$的最短路由这条路径的权重和$V^{\ast }(g)$相加

对顶点$d$来说，有两个选择，可以选择权值为3的路径到$g$，也可以选择权值为1的路径到$f$，取这两种选择里最优选择即可

这样从后往前计算，我们可以得到起点$s$到终点$g$的最短路$V^{\ast }(s)$

1.2 Q函数

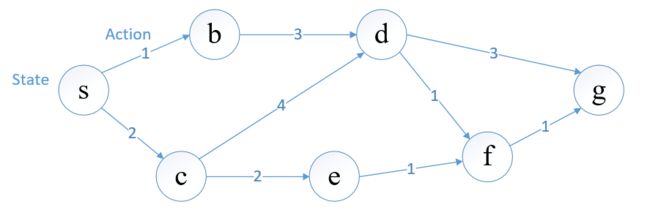
有时我们除了要知道最短路，还要知道最短路这条路径的走向（即怎么走到终点），故我们还需要一个变量记录当前顶点的选择，我们定义$Q^{\ast }(s,a)$为从$s$顶点选择$a$路径到终点$g$的最短路，拿图例来说，顶点$s$出发有两条路径可选，一条权值为1到达$b$，记作$a_1$，一条权值为2到达$c$，记作$a_2$（在强化学习中，我们可以将顶点定义为状态，选择路径定义为动作）

如果$s$选择$a_1$路径，那么$Q^{\ast }(s,a_1)$由这条路权值和$b$到终点的最短路决定
$$Q^{\ast }(s,a_1)=1+V^{\ast }(b)$$
同样对于$a_2$路径，有
$$Q^{\ast }(s,a_2)=2+V^{\ast }(c)$$
对于$s$点到终点的最短路，由这两种选择的最小值决定
$$V^{\ast }(s)=min\{Q^{\ast }(s,a_1),Q^{\ast }(s,a_2)\}$$
我们可以将$V$完全由$Q$函数代替，以$Q^{\ast }(s,a_2)$为例
$$Q^{\ast }(s,a_2)=2+min\{Q^{\ast }(c,a_4),Q^{\ast }(c,a_2)\}$$
现在我们不仅求得了最优值，还记录了每次的选择。

1.3 通过随机性引入期望

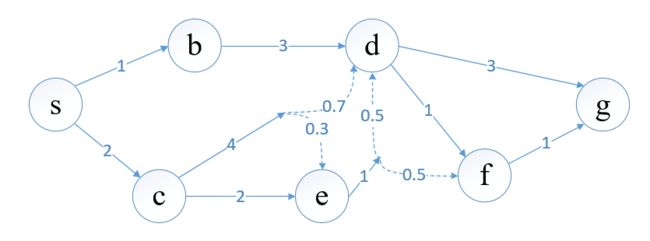
在之前的图中两点之间的到达关系是确定的，现在的图中两点之间具有概率关系，如$c$点选择$a_4$路径有0.7的概率到达$d$，有0.3的概率到达$e$。

从原点到终点，即使策略确定（在每个点选择哪条路是确定的），最终得到的路径值是一个随机变量，因此我们定义最短路为期望最短路。

以$c$为例，如果选择$a_4$路径，期望最短路为
$$Q^{\ast }(c,a_4)=4+0.7\ast min\{Q^{\ast }(d,a_3),Q^{\ast }(d,a_1)\}+0.3\ast Q^{\ast }(e,a_1)$$
抽象化这个式子，顶点由$s$表示，决策由$a$表示，权值由顶点和决策决定，即$r(s,a)$，$p(s^{\prime }|s,a)$表示由当前顶点选择决策到下一个顶点的概率
$$\begin{array}{rl}{Q}^{\ast }(s,a)& =r(s,a)+\sum _{s^{\prime }}[p(s^{\prime }|s,a)\ast mi{n}_{a^{\prime }}{Q}^{\prime }(s^{\prime },a^{\prime })]\\ & =r(s,a)+E_{s^{\prime }\sim p(s^{\prime }|s,a)}[mi{n}_{a^{\prime }}{Q}^{\prime }(s^{\prime },a^{\prime })]\end{array}$$
在强化学习中，我们一般要最大化目标值，即将上式的$min$改为$max$，便得到$Q$函数的最优贝尔曼方程

2. 关于期望

对于强化学习的目标，常常定义为
$$J(\theta )=ma{x}_{\theta }{E}_{\tau \sim p_{\theta }(\tau )}R(\tau )$$
$\tau$表示一条轨迹，可以类比于上面从原点到终点的一条路径，$R(\tau )$表示这条轨迹总的回报值，是一个随机变量，满足$p_{\theta }(\tau )$这个概率分布，最终目标为最大化期望回报值。

$R(\tau )$是轨迹下每一步的决策回报加和，即$R(\tau )={\sum }_{t=0}^{T-1}r(s_t,a_t)$，即$T$个随机变量的和，每一个随机变量$r(s_t,a_t)$由状态动作对$(s_t,a_t)$决定，服从$p_{\theta }(s_t,a_t)$概率分布

对于第一个随机变量$r(s_0,a_0)$
$$p_{\theta }(s_0,a_0)=p(s_0){\pi }_{\theta }(a_0|s_0)p(s_1|s_0,a_0)$$
第二个随机变量$r(s_1,a_1)$
$$p_{\theta }(s_1,a_1)=p(s_0){\pi }_{\theta }(a_0|s_0)p(s_1|s_0,a_0)\pi (a_1|s_1)p(s_2|s_1,a_1)$$
以此类推。

这$T$个随机变量的联合概率分布可以认为是最后一个随机变量的概率分布$p_{\theta }(s_{T-1},a_{T-1})$
$$p_{\theta }(s_{T-1},a_{T-1})=p(s_0)\prod _{t=0}^{T-1}{\pi }_{\theta }(a_t|s_t)p(s_{t+1}|s_t,a_t)$$
也可以认为是该轨迹服从的概率分布

目标函数可以写为
$$J(\theta )=ma{x}_{\theta }{E}_{\tau \sim p_{\theta }(\tau )}\sum _{t=0}^{n-1}r(s_t,a_t)$$
有时为了凸显期望下标显示联合概率分布含义，也写作
$$J(\theta )=ma{x}_{\theta }{E}_{s_0,a_0,s_1\cdots s_T}\sum _{t=0}^{n-1}r(s_t,a_t)$$
我们还知道，期望的和等于和的期望，所以我们可以把求和提到期望外面
$$J(\theta )=ma{x}_{\theta }\sum _{t=0}^{n-1}{E}_{(s_t,a_t)\sim p_{\theta }(s_t,a_t)}r(s_t,a_t)$$
期望的下标也相应换成各自随机变量满足的概率分布

对于无限长度轨迹的情况，我们考虑以下的目标函数
$$J(\theta )=ma{x}_{\theta }{E}_{(s,a)\sim p_{\theta }(s,a)}r(s,a)$$
其中$p_{\theta }(s,a)$表示稳态分布

参考资料

CS 294 Deep Reinforcement Learning

CS 598 Statistical Reinforcement Learning