第九章 动态规划
文章目录
- 动态规划
- 模板问题
- 线性模型
- 区间模型
- 背包模型
- leetcode
- 例1:爬楼梯(70)
- 例2:打家劫舍(198)
- 例3:最大字段和(53)
- 例4:找零钱(322)
- 例5:三角形(120)
- 例6:最长上升子序列(300)
- 例7:最小路径和(64)
- 例8:地牢游戏(174)
- 剑指offer
- 例1:连续子数组的最大和(30)
- 例2:滑动窗口最大值(63)
- 2019校招真题
- 例1:牛牛找工作(1)
- 例2:牛牛的背包问题(8)
动态规划
(1)含义
动态规划(dynamic programming)是运筹学的一个分支,是求解决策过程最优化的数学方法。它基于最优化原理,利用各阶段之间的关系,逐个求解,最终求得全局最优解。在设计动态规划算法时,需要确认原问题与子问题、动态规划状态、边界状态结值、状态转移方程等关键要素。简单来说,动态规划是通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。
在算法面试中,动态规划是最常考察的题型之一,大多数面试官都以是否能较好地解决动态规划相关问题来区分候选是否"聪明"。
(2)基本原理
- 最优子结构
用动态规划求解最优化问题的第一步就是刻画最优解的结构,如果一个问题的解结构包含其子问题的最优解,就称此问题具有最优子结构性质。因此,某个问题是否适合应用动态规划算法,它是否具有最优子结构性质是一个很好的线索。使用动态规划算法时,用子问题的最优解来构造原问题的最优解。因此必须考查最优解中用到的所有子问题。 - 重叠子问题
如果递归算法反复求解相同的子问题,就称为具有重叠子问题(overlapping subproblems)性质。在动态规划算法中使用数组来保存子问题的解,这样子问题多次求解的时候可以直接查表(对于重复子问题,可以将结果保存到一个数组,需要时直接从数组中取值)而不用调用函数递归。
分治与动态规划:
- 相同点
二者都要求原问题具有最优子结构性质,都是将原问题分而治之,分解成若干个规模较小(小到很容易解决的程序)的子问题.然后将子问题的解合并,形成原问题的解. - 不同点
分治法将分解后的子问题看成相互独立的,通过用递归来做。动态规划将分解后的子问题理解为相互间有联系,有重叠部分,需要记忆,通常用迭代来做。
(3)核心思想
理解一个算法就要理解一个算法的核心,动态规划算法的核心是下面的一张图片和一个小故事。

A * "1+1+1+1+1+1+1+1 =?" *
A : "上面等式的值是多少"
B : *计算* "8!"
A *在上面等式的左边写上 "1+" *
A : "此时等式的值为多少"
B : *quickly* "9!"
A : "你怎么这么快就知道答案了"
A : "只要在8的基础上加1就行了"
A : "所以你不用重新计算因为你记住了第一个等式的值为8!动态规划算法也可以说是 '记住求过的解来节省时间'"
由上面的图片和小故事可以知道动态规划算法的核心就是记住已经解决过的子问题的解。
(4)基本思路
若要解一个给定问题,我们需要解其不同部分(即子问题),再合并子问题的解以得出原问题的解。 通常许多子问题非常相似,为此动态规划法试图仅仅解决每个子问题一次,从而减少计算量: 一旦某个给定子问题的解已经算出,则将其记忆化存储,以便下次需要同一个子问题解之时直接查表。 这种做法在重复子问题的数目关于输入的规模呈指数增长时特别有用。
实现步骤:
- 确认原问题与子问题
- 描绘问题的解结构(一般通过一维/二维DP数组)并确认一般状态(DP[i]的意义)
- 确认边界状态的值(可理解为递归出口) & 状态转移方程(由边界状态推出一般状态的规律,可理解为递归函数)
状态转移方程一般通过自顶向下递归分析,再自底向上动态规划推导得出。
(5)两种形式
上面已经知道动态规划算法的核心是记住已经求过的解,记住求解的方式有两种:①自顶向下的备忘录法 ②自底向上。
为了说明动态规划的这两种方法,举一个最简单的例子:求斐波拉契数列Fibonacci 。先看一下这个问题:
Fibonacci (n) = 1; n = 0
Fibonacci (n) = 1; n = 1
Fibonacci (n) = Fibonacci(n-1) + Fibonacci(n-2)
以前学c语言的时候写过这个算法使用递归十分的简单。先使用递归版本来实现这个算法:
public int fib(int n)
{
if(n<=0)
return 0;
if(n==1)
return 1;
return fib( n-1)+fib(n-2);
}
//输入6
//输出:8
先来分析一下递归算法的执行流程,假如输入6,那么执行的递归树如下:
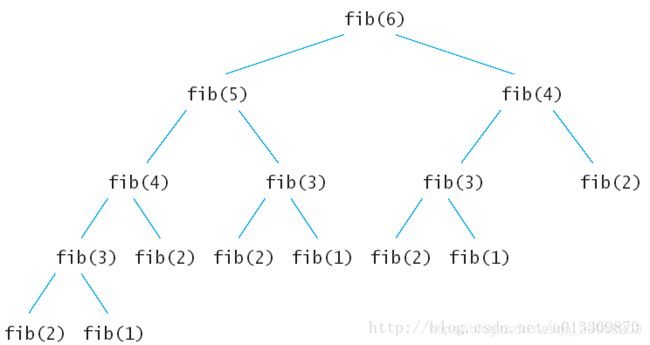
上面的递归树中的每一个子节点都会执行一次,很多重复的节点被执行,fib(2)被重复执行了5次。由于调用每一个函数的时候都要保留上下文,所以空间上开销也不小。这么多的子节点被重复执行,如果在执行的时候把执行过的子节点保存起来,后面要用到的时候直接查表调用的话可以节约大量的时间。下面就看看动态规划的两种方法怎样来解决斐波拉契数列Fibonacci 数列问题。
①自顶向下的备忘录法
public static int Fibonacci(int n)
{
if(n<=0)
return n;
int []Memo=new int[n+1];
for(int i=0;i<=n;i++)
Memo[i]=-1;
return fib(n, Memo);
}
public static int fib(int n,int []Memo)
{
if(Memo[n]!=-1)
return Memo[n];
//如果已经求出了fib(n)的值直接返回,否则将求出的值保存在Memo备忘录中。
if(n<=2)
Memo[n]=1;
else Memo[n]=fib( n-1,Memo)+fib(n-2,Memo);
return Memo[n];
}
备忘录法也是比较好理解的,创建了一个n+1大小的数组来保存求出的斐波拉契数列中的每一个值,在递归的时候如果发现前面fib(n)的值计算出来了就不再计算,如果未计算出来,则计算出来后保存在Memo数组中,下次在调用fib(n)的时候就不会重新递归了。比如上面的递归树中在计算fib(6)的时候先计算fib(5),调用fib(5)算出了fib(4)后,fib(6)再调用fib(4)就不会在递归fib(4)的子树了,因为fib(4)的值已经保存在Memo[4]中。
②自底向上的动态规划
备忘录法还是利用了递归,上面算法不管怎样,计算fib(6)的时候最后还是要计算出fib(1),fib(2),fib(3)……,那么何不先计算出fib(1),fib(2),fib(3)……,呢?这也就是动态规划的核心,先计算子问题,再由子问题计算父问题。
public static int fib(int n)
{
if(n<=0)
return n;
int []Memo=new int[n+1];
Memo[0]=0;
Memo[1]=1;
for(int i=2;i<=n;i++)
{
Memo[i]=Memo[i-1]+Memo[i-2];
}
return Memo[n];
}
自底向上方法也是利用数组保存了先计算的值,为后面的调用服务。观察参与循环的只有 i,i-1 , i-2三项,因此该方法的空间可以进一步的压缩如下。
public static int fib(int n)
{
if(n<=1)
return n;
int Memo_i_2=0;
int Memo_i_1=1;
int Memo_i=1;
for(int i=2;i<=n;i++)
{
Memo_i=Memo_i_2+Memo_i_1;
Memo_i_2=Memo_i_1;
Memo_i_1=Memo_i;
}
return Memo_i;
}
一般来说由于备忘录方式的动态规划方法使用了递归,递归的时候会产生额外的开销,使用自底向上的动态规划方法要比备忘录方法好。
自顶向下备忘录法从结果(父问题)出发,逐步向下寻找出口(子问题)。它的本质还是递归,计算递归的过程可能有O(2^n)复杂度,它将结果存储在备忘录数组中。下一次调用相同结果可以直接从备忘录数组中获取。
自底向上动态规划根据规律,从递归出口(子问题)出发(已知),设计动态规划数组,逐渐寻找父问题的解。
其实,动态规划应该先自顶向下思考,再自底向上求得结果。
(6)实例
例1 最优解问题1——求能赚最多钱
题目描述
![]()
共有8个任务,如图为每个任务执行起始时间与结束时间,以及做完每件事情可赚金钱。
要求:执行每个任务的时间不能重叠
求如何选择执行任务能够赚最多钱?
解题思路
能够赚最多金钱——最优解问题,可通过定义最优解数组完成
最优解数组即 包含i个子问题的最优解。这里可理解为:可执行i个任务所能够赚的最多钱。
先自顶向下分析:一共有8个任务,每个任务都有2种状态:选/不选。选择该任务则可将多赚该任务的价值,但不能选择与该任务重叠时间的任务;不选该任务则无法赚得该任务的价值,对其余任务没有影响。例如对于OPT(8)而言即求共有8个任务时最多能够赚的金钱,如果选择了第8个任务,则可赚4元(arr[8]=4)且剩下只能选择前5个任务(prev[8]=5),此时最优解(最多可赚金钱)应该为前5个任务最多可赚金钱+第8个任务可赚金钱=OPT(5)+4;如果没有选择第8个任务,则不赚任何钱,选择前7(8-1)个任务可赚最多钱=OPT(7)。因此,含有8个任务的最优解为max(OPT(5)+4,opt(7))。剩下依此类推,可画出递归树:
![]()
由递归树,可总结出一般规律,即:
OPT(i) = max(OPT(i-1) , OPT(prev()) + arr[i])
递归出口为:
OPT(0) = arr[0]; //只有一个任务时一定选择该任务能得到最优解
因此这里的8个任务可看做具有最优子结构(max(选/不选))的重叠子问题(都可用以上最优解方程求得最优解)。
程序代码
(1)自顶向下递归备忘录
public int BestSolution1(List list) {
//存储解决i个问题时的最优解,即需要执行i个任务可赚得最多金钱,由递归树可得代码
int[] OPT = new int[list.size()];
//初始化前置数组,即如果选择了第i个任务,则下一次只能选择前prev[i]个任务
int[] prev = new int[list.size()];
for(int i=list.size()-1;i>=0;i--) {
Integer startTime = list.get(i).startTime;
prev[i] = -1;
for(int j = i-1;j>=0;j--) {
//往前遍历,选取之前第一个结束时间在该任务开始事件之前的任务。
Integer endTime = list.get(j).endTime;
if(endTime<=startTime) {
prev[i] = j;
break;
}
}
}
int result = mem_BestSolution1(list,prev,OPT);
return result;
}
public int mem_BestSolution1(List list,int[] prev,Integer i,int[] OPT) {
//自顶向下备忘录法求得解决第i个问题时的最优解
//递归思想,复杂度为O(2^n)
//递归出口,第1个任务的最优解一定是执行完第一个任务所赚的钱
if(i<0) return 0;//i<0表示没有需要执行的任务,最优解(能赚的最多钱)=0
else if(i==0) OPT[0] = list.get(0).value;
else {
//其余任务则根据总结出的一般规律得出
int choose_A = mem_BestSolution1(list,prev,i-1,OPT);//不选择第i个任务时取前i-1个任务的最优解
int choose_B = mem_BestSolution1(list,prev,prev[i],OPT) + list.get(i).value;//选择第i个任务时取前prev[i]任务最优解 + 该任务所赚的钱
OPT[i] = max(choose_A,choose_B);//取 选/不选 该任务的最大值 即为最优解
}
return OPT[i];
}
public int max(int a,int b) {
//获取a,b中最大值
return a>=b?a:b;
}
public static class Task{
Integer startTime; //起始时间
Integer endTime; //结束时间
Integer value; //可赚金钱
public Task(Integer startTime,Integer endTime,Integer value){
this.startTime = startTime;
this.endTime = endTime;
this.value = value;
}
}
(2)自底向上动态规划
public int BestSolution1(List list) {
//存储解决i个问题时的最优解,即需要执行i个任务可赚得最多金钱,由递归树可得代码
int[] OPT = new int[list.size()];
//初始化前置数组,即如果选择了第i个任务,则下一次只能选择前prev[i]个任务
int[] prev = new int[list.size()];
for(int i=list.size()-1;i>=0;i--) {
Integer startTime = list.get(i).startTime;
prev[i] = -1;
for(int j = i-1;j>=0;j--) {
//往前遍历,选取之前第一个结束时间在该任务开始事件之前的任务。
Integer endTime = list.get(j).endTime;
if(endTime<=startTime) {
prev[i] = j;
break;
}
}
}
int result = dp_BestSolution1(list,prev,OPT);
return result;
}
public int dp_BestSolution1(List list,int[] prev,int[] OPT) {
//自底向上动态规划求得解决第i个问题时的最优解
//遍历思想,复杂度为O(n)
//递归出口,第1个任务的最优解一定是执行完第一个任务所赚的钱
Integer task_number = list.size();
OPT[0] = list.get(0).value;//最小子问题
for(int i = 1;ichoose_B?choose_A:choose_B;//取 选/不选 该任务的最大值 即为最优解
}
return OPT[task_number-1];
}
public int max(int a,int b) {
//获取a,b中最大值
return a>=b?a:b;
}
public static class Task{
Integer startTime; //起始时间
Integer endTime; //结束时间
Integer value; //可赚金钱
public Task(Integer startTime,Integer endTime,Integer value){
this.startTime = startTime;
this.endTime = endTime;
this.value = value;
}
}
例2 最优解问题2——求所选数组求和最大值
题目描述

选择一堆数字,要求:
- 当选择第i个数字时,不能选择相邻的两个数字(不能选择第i+1和第i-1个数字)
- 使所选数字的和最大
解题思路
求和的最大值,即最优解问题。可用例1的思路求解。通过定义最优解数组来存储重复子问题进行求解。
定义一个最优解数组,数组中每个元素存储 包含 i 个子问题时的最优解,本题可理解为 含有 i+1 个元素的数组所能取到的最大值。
OPT(i) = 长度为 i + 1 的数组的最佳方案
自顶向下分析:对于 i = 6 位置的数字,有两种处理方式:选/不选。如果选择该数字,则最优解加上该数字的值,但不能选 i = 5 位置的数字,此时只能取 i <= 4 位置的最优解,即求含有5个元素的数组的最优解,因此该情况下最优解为:arr[6] + OPT(4),如果没有选择该数字,则和不变,取前6个位置的最优解,因此该情况下最优解为:OPT(5)。因此,i = 6时的最优解为选或不选两种情况下最优解的最大值。即,OPT(6) = max(OPT(5),OPT(4)+arr[6]),同理可绘制递归树:
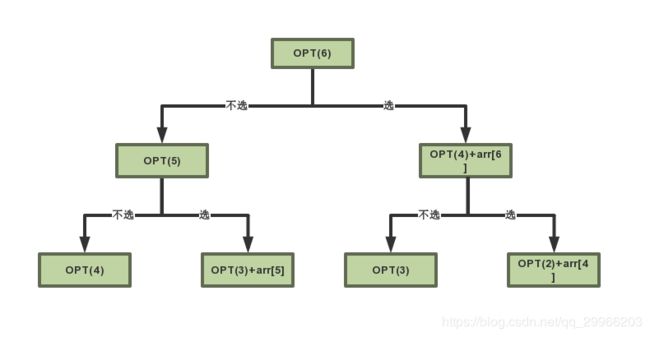
由递归树可得一般规律:
OPT(i) = max(OPT(i-1),OPT(i-2) + arr[i])
递归出口为:
OPT(0) = arr[0]
OPT(1) = max(arr[0],arr[1])
因此这里的长度为7的数组可看做具有最优子结构(max(选/不选))的重叠子问题(看成长度为1、2、3…的数组,这些数组(子问题)都可用以上最优解方程求得最优解)。
程序代码
(1)自顶向下递归备忘录
public int BestSolution2(int[] arr) {
//存储解决i+1个问题时的最优解,opt[i]中存储长度为i+1的数组求和所得最大值,由递归树可得代码
int[] OPT = new int[arr.length];
return dp_BestSolution2(arr,OPT);
}
public int mem_BestSolution2(int[] arr,int[] OPT,int i) {
//自顶向下备忘录法,采用递归方式求解,递归算法,需要用i来指定递归的层次
//递归出口
if(i == 0) {
OPT[i] = arr[0];//如果数组中只有1个元素,则返回第一个元素的值
}
else if(i == 1) {
OPT[i] = max(arr[0],arr[1]); //如果数组中含有2个元素,则返回第一个元素或第二个元素
}
else {
// 其余情况,根据递归树规律。含有 i 个元素的数组的最优解为
// 含有 i-1 个元素的数组的最优解(不选择第 i 个元素)
// 含有 i-2 个元素的数组的最优解 + 第 i-1 个元素取值
// 的最大值
OPT[i] = mem_BestSolution2(arr,OPT,i-1);
OPT[i] = mem_BestSolution2(arr,OPT,i-2) + arr[i];
}
return OPT[i];
}
(2)自底向上动态规划
public int BestSolution2(int[] arr) {
//存储解决i+1个问题时的最优解,opt[i]中存储长度为i+1的数组求和所得最大值,由递归树可得代码
int[] OPT = new int[arr.length];
return dp_BestSolution2(arr,OPT);
}
public int dp_BestSolution2(int[] arr,int[] OPT) {
// 自底向上动态规划,采用遍历思想
// 从已知底端,即长度为1的元素出发
OPT[0] = arr[0];
OPT[1] = max(arr[0],arr[1]);
//遍历
for(int i=2;i例3 最优解问题3——求是否存在所选数组求和=给定值
题目描述
![]()
对于数组arr,取出一组数字,且不能取相邻数字,是否存在方案使得所取数字之和 = S?若存在,则返回true,否则返回false。
解题思路
采用动态规划思想,定义数组subset[],第 i 个位置的元素表示包含 i 个元素的数组是否存在方案使所取数字和 = S,若存在方案使数字和 = S,则返回true,否则返回false。
采用自顶向下的思想进行分析:
对于长度为 8 的数组arr,第8个元素包含选或不选两种情况:如果选择第 8 个元素,则此时解为求解长度为7的数组arr存在数字和 = S - 第8个元素;如果不选第8个元素,则此时解为求解长度为7的数组arr存在数字和 = S。长度为 8 的数组arr存在数字和为 S 的解为 这两种情况取或(只要有一种成立即可),长度为7的数组arr,长度为6的数组arr…可用相同的思想分析,因此得一般规律
subset(i,S) = subset(i-1,S) || subset(i-1,S-arr[i])
递归出口为(递归出口的情况应该分析完整)
if(S == 0)return true;//如果取到0,则说明存在方案使取值=S
if(i == 0){
/*
if(arr[i] == S)return true;
else return false;//遍历到第一个元素,若第一个元素=S,则存在方案,否则不存在方案
*/
return arr[i] == S;
}
if(arr[i]>S)return subset(i-1,S);//若该元素大于S,则一定不选该元素
程序代码
(1)自顶向下递归备忘录
public boolean BestSolution3(int[] arr,int S) {
// 存储解决i个问题时的最优解,即长度为i的数组是否能够取一组数字,使得数字求和 = S
// 这里最优解数组为二维数组,由于每个子问题包含两个变量,一个为数组长度,一个为求和S大小,横坐标表示长度为i的数组,纵坐标表示求和S
// 即对于最优解数组SUBSET[i][j]表示长度为 i+1 的数组是否存在数字和为 j 的一组数
boolean[][] SUBSET = new boolean[arr.length][S+1];
boolean result = mem_BestSolution3(arr,S,arr.length-1,SUBSET);
//boolean result = dp_BestSolution3(arr,S,SUBSET);
return result;
}
public boolean mem_BestSolution3(int[] arr,int S,int i,boolean[][] SUBSET) {
//采用自顶向下备忘录法进行回溯
//每一次递归求的是包含 i+1 个元素的数组arr是否存在和为 S 的一组数
if(S == 0)SUBSET[i][0] = true;//若求和S=0,则一定存在方案(剩下均不选)
else if(i==0)
{
if(arr[0] == S)SUBSET[0][S] = true;
else SUBSET[0][S] = false;//如果数组只含有1个元素,若该元素=S,则存在方案,否则不存在方案
}
else if(arr[i] > S) {
//若该元素大于所需求和S,则求不选这个元素时的方案(取包含i-1个元素的数组方案)
SUBSET[i][S] = mem_BestSolution3(arr,S,i-1,SUBSET);
}
else {
// 不选该元素时,取包含 i-1 个元素是否存在求和为 S 的方案
// 选该元素时,取包含 i-1 个元素是否存在求和为 S-arr[i] 的方案
// 包含 i 个元素时的解为这两种方案求解的或
SUBSET[i][S] = (mem_BestSolution3(arr,S-arr[i],i-1,SUBSET) || mem_BestSolution3(arr,S,i-1,SUBSET));
}
return SUBSET[i][S];
}
(2)自底向上动态规划
public boolean BestSolution3(int[] arr,int S) {
// 存储解决i个问题时的最优解,即长度为i的数组是否能够取一组数字,使得数字求和 = S
// 这里最优解数组为二维数组,由于每个子问题包含两个变量,一个为数组长度,一个为求和S大小,横坐标表示长度为i的数组,纵坐标表示求和S
// 即对于最优解数组SUBSET[i][j]表示长度为 i+1 的数组是否存在数字和为 j 的一组数
boolean[][] SUBSET = new boolean[arr.length][S+1];
boolean result = mem_BestSolution3(arr,S,arr.length-1,SUBSET);
//boolean result = dp_BestSolution3(arr,S,SUBSET);
return result;
}
public boolean dp_BestSolution3(int[] arr,int S,boolean[][] SUBSET) {
//采用自底向上动态规划,从已知开始构造求解数组
//当S=0时,则一定存在方案。即SUBSET[i][0](0<=i<=arr.length-1)
for(int i=0;i<=arr.length-1;i++)SUBSET[i][0] = true;
//当i=0时,若arr[0]==S则一定存在,否则不存在
for(int j=1;j<=S;j++) {
if(arr[0] == j)SUBSET[0][j] = true;
else SUBSET[0][j] = false;
}
for(int i=1;i<=arr.length-1;i++)
for(int j=1;j<=S;j++) {
//遍历法求解
if(arr[i]>j)SUBSET[i][j] = SUBSET[i-1][j];
else {
SUBSET[i][j] = (SUBSET[i-1][j] || SUBSET[i-1][j-arr[i]]);
}
}
return SUBSET[arr.length-1][S];
}
模板问题
线性模型
区间模型
背包模型
leetcode
例1:爬楼梯(70)
题目描述
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
注意:给定 n 是一个正整数。
示例 1:
输入: 2
输出: 2
解释: 有两种方法可以爬到楼顶。
1. 1 阶 + 1 阶
2. 2 阶
示例 2:
输入: 3
输出: 3
解释: 有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶
动态规划原理
- 确认原问题与子问题
原问题为求n阶台阶所有走法的数量,子问题是求1阶台阶、2阶台阶、…、n-1阶台阶的走法。 - 确认状态
本题的动态规划状态单一,第i个状态即为i阶台阶的所有走法数量。 - 确认边界状态的值
边界状态为1阶台阶与2阶台阶的走法,1阶台阶有1种走法,2阶台阶有2种走法,即dp[1]=1;dp[2]=2; - 确认状态转移方程
将求第i个状态的值转移为求第i-1个状态的值与第i-2个状态的值,动态规划转移方程为dp[i]=dp[i-1]+dp[i-2] (i>=3)
算法思路
- 设置递推数组dp[0…n],dp[i]代表到达第i阶,有多少种走法。初始化数组元素为0
- 设置到达第1阶台阶有1种走法,到达第2阶台阶有2种走法
dp[1] = 1;dp[2] = 2; - 利用循环递推从第3阶台阶至n阶台阶结果:
到达第i阶台阶的方式数 = 到达第i-1阶台阶的方式数 + 到达第i-2阶台阶的方式数
dp[i] = dp[i-1] + dp[i-2]
程序代码
public int climbStairs(int n) {
// 采用自底向上动态规划解决问题
// dp[i] 表示爬 i 个台阶有dp[i]种方法,则对于第 i 个台阶可以从第i-1个台阶爬1个台阶或者从第i-2个台阶爬2个台阶
// 边界情况为爬 1 个台阶时有一种方法,爬 2 个台阶有两种方法
// 根据状态边界与状态转移方程得到dp代码
if(n==0)return 0;
if(n==1)return 1;
if(n==2)return 2;
else {
int[] dp = new int[n+1];//dp[i]表示爬i级台阶的方法
dp[0] = 0;// 0级台阶没有方案
dp[1] = 1;// 爬1级台阶时候,只有一种方法
dp[2] = 2;// 爬2级台阶时可以 爬2次一级台阶或爬一次2级台阶
for(int i=3;i<=n;i++) {
// 爬i级台阶可以从i-1级台阶爬1级或者从i-2级台阶爬2级
// 因此爬i级台阶的方法是爬 i-2 级台阶的方法 + 爬 i 级台阶的方法
dp[i] = dp[i-1] + dp[i-2];
}
return dp[n];
}
}
例2:打家劫舍(198)
题目描述
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你在不触动警报装置的情况下,能够偷窃到的最高金额。
示例 1:
输入: [1,2,3,1]
输出: 4
解释: 偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。
示例 2:
输入: [2,7,9,3,1]
输出: 12
解释: 偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9),接着偷窃 5 号房屋 (金额 = 1)。偷窃到的最高金额 = 2 + 9 + 1 = 12 。
算法思路
- 确认原问题与子问题
原问题为求n个房间的最优解,子问题为求前1个房间,前2个房间,…,前n-1个房间的最优解 - 确认状态
第i个状态即为前i个房间能够获得的最大财宝(最优解) - 确认边界状态的值
前1个房间的最优解为前1个房间的财宝;
前2个房间的最优解为第1,2个房间中较大财宝; - 确认状态转移方程
方案1:选择第i个房间:前i-1个房间,前i-2个房间的最优解
方案2:不选择第i个房间:前i-1个房间的最优解
则动态规划转移方程为:dp[i] = max(dp[i-1],dp[i-2]+nums[i])(i>=3)
程序代码
public int rob(int[] nums) {
// 采用自底向上动态规划解决问题
// dp[i]表示共有i个房间时可以偷窃的最高金额,对于第i个房间,有选/不选2种方式,要么选择要么不选
// 如果选择的话,由于不能偷窃相邻的房间的金额,因此此时 dp[i] = dp[i-2] + nums[i]
// 如果不选择的话,则相当于求前 i-1 个房间的金额,因此此时dp[i] = dp[i-1]
// 边界情况为dp[0] = nums[0];dp[1] = max(nums[0],nums[1]);
int[] dp = new int[nums.length];
if(nums.length == 0)return 0;//没有金额时,可偷金额为0
if(nums.length == 1)return nums[0];
if(nums.length == 2)return max(nums[0],nums[1]);
else {
dp[0] = nums[0];//只有1个房间时,可偷金额为该房间可偷窃金额
dp[1] = max(nums[0],nums[1]);//有2个房间时,可偷金额为偷该房间的金额或偷第一个房间的金额
for(int i=2;i<=nums.length-1;i++) {
dp[i] = max(dp[i-2] + nums[i],dp[i-1]);//遍历剩余情况,选择该房间/不选该房间状态
}
return dp[nums.length-1];
}
}
public int max(int a,int b) {
return a>=b?a:b;
}
例3:最大字段和(53)
题目描述
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
示例:
输入: [-2,1,-3,4,-1,2,1,-5,4],
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
算法思路
这道题的难点在于,如何确定第i个状态(dp[i])?如果设置第i个状态(dp[i])代表前i个数字组成的连续最大字段和,并能根据dp[i-1]、dp[i-2]、…、dp[0]推导出dp[i]。
但发现dp[i]与dp[i-1]并不相邻,dp[i]无法通过dp[i-1]构成连续子数组,之间没有内在联系,因此无法推导。
为了让第i个状态的最优解与第i-1个状态的最优解产生直接联系,思考:如果让第i个状态(dp[i])代表以第i个数字结尾的最大子段和,那么dp[i]与dp[i-1]之间的关系是否可以推导?如何由此推出最终结果?
将求n个数的数组的最大子段和转换为分别求第1个、第2个、…、第i个、…、第n个数字结尾的最大子段和,再找出这n个结果中最大的作为结果,动态规划算法:
第i个状态(dp[i])即为以每个数字结尾的最大子段和(最优解)。由于以第i-1个数字结尾的最大子段和(dp[i-1])与nums[i]相邻,故动态规划转移方程为:
若dp[i-1]>0;dp[i] = dp[i-1] + nums[i];
否则dp[i] = nums[i];
边界值:以第1个数字结尾的最大子段和dp[0] = nums[0]
程序代码
public int max(int a,int b) {
return a>=b?a:b;
}
//53.最大子序和
//给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
public int maxSubArray(int[] nums) {
// 创建最优解数组,即满足最优子结构及重复子结构
// 第i个状态dp[i]表为以第i个数字结尾的连续数字段的最大和。则求连续数字段的最大和即求max(dp)
// 一般规律为:dp[i] = max(nums[i],dp[i-1]+nums[i])
// 边界为:dp[0] = nums[0]
if(nums.length == 0)return 0;
if(nums.length == 1)return nums[0];
else {
int[] dp = new int[nums.length];
dp[0] = nums[0];//若数组中只有一个元素,则最大和为该元素的值
int max_res = dp[0];
for(int i=1;i<=nums.length-1;i++) {
// 其余元素遍历求解,要么选,要么不选
// 对于dp[i]表示以第i个元素为连续子数组的最后一个数字时的最大和
// 即只选择最后一个数字或者以前一个数字为最后一个数字的连续数字段
dp[i] = max(dp[i-1]+nums[i],nums[i]);
// 此时整数数组中的连续子数组的最大和为dp中最大值
if(dp[i]>max_res) {
max_res = dp[i];
}
}
return max_res;
}
}
例4:找零钱(322)
题目描述
给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回 -1。
示例 1:
输入: coins = [1, 2, 5], amount = 11
输出: 3
解释: 11 = 5 + 5 + 1
示例 2:
输入: coins = [2], amount = 3
输出: -1
说明:
你可以认为每种硬币的数量是无限的。
算法思路
- 是否可以用贪心?
钞票面值为[1,2,5,7,10],金额为14,最优解需要2张7元。如果用贪心思想,每次优先使用较大面值的金额,选1张10元,剩下4元选2张2元。一共用3张。错解。
因此贪心思想在个别面值组合是可以的(如[1,2,5,10,20,50,100]),但本题面值不确定,因此不能用贪心思想。 - 采用动态规划的解决方案?
分析钞票面值coins=[1,2,5,7,10],金额:14
dp[i]代表金额i的最优解(即最少使用钞票的数量)。在计算dp[i]时,dp[0]、dp[1]、dp[2]、…、dp[i-1]都是已知的:而金额i可由:
金额 i-1 与coins[0](1)组合;
金额 i-2 与coins[1](2)组合;
金额 i-5 与coins[2](5)组合;
金额 i-7 与coins[3](7)组合;
金额 i-10 与coins[4](10)组合;
即状态可由状态i-1、i-2、i-5、i-7、i-10这5个状态转移到,因此dp[i] = min(dp[i-1],dp[i-2],dp[i-5],dp[i-7],dp[i-10]) + 1
程序代码
public int coinChange(int[] coins, int amount) {
// dp[i] 代表金额i的最优解(即凑成金额 i 的最小使用钞票数)
// 假设对于[1,2,5,7,10] 若需要的最小钞票数i 即为 (i-1,i-2,i-5,i-7,i-10 所需要的最小钞票数)中最小值 + 1
// 即若可通过添加某个硬币获得金额 i ,则金额 i 的状态为获取该硬币前的状态 加上 该硬币
// 即金额i的最优解(所需最少钞票数) = 获取该硬币前的最优解(所需最少钞票数) + 1
// dp[i] = min( dp[i-1],dp[i-2],dp[i-5],dp[i-7],dp[i-10]) + 1
int[] dp = new int[amount+1];//dp[i]表示金额为i时的最优解(最少使用的钞票数目)
for(int i=0;i<=amount;i++)
dp[i] = -1;//初始化dp数组,最初所有金额的初始值均为-1,表示不可到达
dp[0]=0;//金额为0的最优解为0
for(int i=1;i<=amount;i++) {//遍历所有金额,对1~所求金额求最优解
for(int j=0;j= coins[j] && dp[i-coins[j]] != -1) {//若所求金额>硬币的值(可通过添加硬币得到金额i) 且 获取硬币前的状态可达
if(dp[i] > dp[i-coins[j]]+1 || dp[i]==-1) {//若该方案比之前取硬币方案所需硬币数更小 或者 为第一个方案
dp[i] = dp[i-coins[j]]+1;//取所有方案的最小值
}
}
}
}
return dp[amount];//返回金额为amount的最优解
}
例5:三角形(120)
题目描述
给定一个三角形,找出自顶向下的最小路径和。每一步只能移动到下一行中相邻的结点上。
例如,给定三角形:
[
[2],
[3,4],
[6,5,7],
[4,1,8,3]
]
自顶向下的最小路径和为 11(即,2 + 3 + 5 + 1 = 11)。
- 设置一个二维数组,最优解三角形dp[][],并初始化数组元素为0,dp[i][j]代表从底向上递推时,走道三角形第i行第j列的最优解。
- 从三角形的底部向三角形上方进行动态规划:
a. 动态规划边界条件:底端上的最优解即为数字三角形的最后一层
b.利用i循环,从倒数第二层递推至第一层,对于每层的各列,进行动态规划递推:
第i行,第j列的最优解为dp[i][j] = min(dp[i+1][j],dp[i+1][j+1]) + triangle[i][j] - 返回dp[0][0]
程序代码
public int minimumTotal(List> triangle) {
// 构造二维数组,dp[i][j]表示自底向上递推,走到三角形第i行j列时的最优解
// 自顶向下推到三角形第i行j列位置时的最小路径和 的逆推
// 转换数据类型->方便处理
int length = triangle.get(triangle.size()-1).size();// 三角形最后一行的长度
int[][] dp = new int[length][length];// 三角形的最优解数组
//初始化
for(int i=0;i row = triangle.get(i);
for(int j=0;j=0;i--) {
List row = triangle.get(i);
for(int j=0;j=b?b:a;
}
法2
int[][] tri; // 原三角形二维数组形式
int[][] tri_sum; // 原三角形路径和形式
int length;
public int minimumTotal(List<List<Integer>> triangle) {
// 将List> 转化为二维数组形式
if(triangle == null || triangle.size() == 0)return 0;
length = triangle.size();
tri = new int[length][length];
tri_sum = new int[length][length];
for(int i=0;i<length;i++) {
for(int j=0;j<=i;j++) {
tri[i][j] = triangle.get(i).get(j);
}
}
constructTriSum();
int min = tri_sum[length-1][0];
for(int i=1;i<length;i++)
if(tri_sum[length-1][i]<min)min = tri_sum[length-1][i];
return min;
}
public void constructTriSum() {
// 自底向上备忘录
// tri_sum[i][j] 表示到tri[i][j]时路径的最小值
tri_sum[0] = tri[0];
for(int i=1;i<length;i++) {
// 每一行的首元素和尾元素单独处理
tri_sum[i][0] = tri_sum[i-1][0] + tri[i][0];
tri_sum[i][i] = tri_sum[i-1][i-1] + tri[i][i];
for(int j=1;j<i;j++) {
// 中间元素为左上和上部元素较小值加上本身
tri_sum[i][j] =Integer.min(tri_sum[i-1][j-1],tri_sum[i-1][j])+tri[i][j];
}
}
}
例6:最长上升子序列(300)
题目描述
给定一个无序的整数数组,找到其中最长上升子序列的长度。
示例:
输入: [10,9,2,5,3,7,101,18]
输出: 4
解释: 最长的上升子序列是 [2,3,7,101],它的长度是 4。
算法思路
若第i个状态dp[i]代表前i个元素中最长上升子序列的长度,则dp[i-1]代表前i-1个元素中最长上升子序列的长度,则dp之间没有直接联系,无法递推。
若第i个状态dp[i]代表以第i个元素结尾的最长上升子序列的长度,则nums[i]一定是dp[i]所对应的最长上升子序列中最大元素(位于末尾),最终结果为dp[0],dp[1],dp[2],…,dp[i],…,dp[n-1]中的最大值
设置动态规划数组dp[],第i个状态dp[i]代表以第i个元素结尾的最长上升子序列的长度:
动态规划边界:dp[0] = 1;
初始化最长上升子序列的长度LIS = 1;
从1到n-1,循环i,极端dp[i];
从0至i-1,循环j,若nums[i]>nums[j],说明nums[i]可放置在nums[j]的后面,组成最长上升子序列:
若dp[i] < dp[j]+1;
dp[i] = dp[j] +1
LIS为dp[0],dp[1],…,dp[i],…,dp[n-1]中最大的。
程序代码
public int lengthOfLIS(int[] nums) {
// dp[i]动态规划数组表示以第 i 个元素结尾的最长上升子序列的长度
// 对于dp[i] 中对应的第 i 个元素 nums[i] 一定为dp[i]的最大值,即最后一个元素。
// 因此应在 nums 数组中寻找小于nums[i] 的元素,则 nums[i] 一定可以排在这些元素后面作为一个新的上升子序列
// 因此以 nums[i] 为结尾(最大值)的最长上升子序列一定为这些上升子序列的长度中最大的
// 即设 min_nums[] 为nums[] 中小于nums[i] 的数组
// 则 dp[i] = max(min_nums[]) + 1;
if(nums.length == 0) return 0;//原数组长度为0,则其最长子序列长度为0
int dp[] = new int[nums.length];
//初始化,默认以第 i 个元素为结尾的上升子序列长度为 1(自身)
for(int i=0;i=0;j--) {
if(nums[j]max)max = dp[i];
return max;
}
例7:最小路径和(64)
题目描述
给定一个包含非负整数的 m x n 网格,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
示例:
输入:
[
[1,3,1],
[1,5,1],
[4,2,1]
]
输出: 7
解释: 因为路径 1→3→1→1→1 的总和最小。
算法思路
- 定义一个动态规划二维数组dp[][],其中dp[i][j]表示移动到网格grid[i][j]时最小路径的值
- 因为每次只能向下或者向右移动一步,因此dp[i][j]的状态一定是从dp[i-1][j]或者dp[i][j-1]转移
- 则dp[i][j] = min(dp[i-1][j],dp[i][j-1]) + grid[i][j];
程序代码
public int minPathSum(int[][] grid) {
// 定义一个动态规划二维数组dp[][],其中dp[i][j]表示移动到网格grid[i][j]时最小路径的值
// 因为每次只能向下或者向右移动一步,因此dp[i][j]的状态一定是从dp[i-1][j]或者dp[i][j-1]转移
// 则dp[i][j] = min(dp[i-1][j],dp[i][j-1]) + grid[i][j];
// 初始状态 dp[0][0] = grid[0][0];
// 第一行的数据只能一直向右,第一列的数据只能一直向下
// 故第一行与第一列数据也可初始化得出
if(grid.length == 0)return 0;//网格为空,最小路径和为0
int grid_row = grid.length;//网格行数
int grid_col = grid[0].length;//网格列数
int[][]dp = new int[grid_row][grid_col];
for(int i =0;i=b?b:a;
}
例8:地牢游戏(174)
题目描述
一些恶魔抓住了公主(P)并将她关在了地下城的右下角。地下城是由 M x N 个房间组成的二维网格。我们英勇的骑士(K)最初被安置在左上角的房间里,他必须穿过地下城并通过对抗恶魔来拯救公主。
骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻降至 0 或以下,他会立即死亡。
有些房间由恶魔守卫,因此骑士在进入这些房间时会失去健康点数(若房间里的值为负整数,则表示骑士将损失健康点数);其他房间要么是空的(房间里的值为 0),要么包含增加骑士健康点数的魔法球(若房间里的值为正整数,则表示骑士将增加健康点数)。
为了尽快到达公主,骑士决定每次只向右或向下移动一步。
编写一个函数来计算确保骑士能够拯救到公主所需的最低初始健康点数。
例如,考虑到如下布局的地下城,如果骑士遵循最佳路径 右 -> 右 -> 下 -> 下,则骑士的初始健康点数至少为 7。
| -2 | -3 | 3 |
|---|---|---|
| -5 | -10 | 1 |
| 10 | 30 | -5 |
说明:
骑士的健康点数没有上限。
任何房间都可能对骑士的健康点数造成威胁,也可能增加骑士的健康点数,包括骑士进入的左上角房间以及公主被监禁的右下角房间。
算法思路
从右下向左上递推:
dp[i][j]代表若要到达右下角,至少有多少血量,能在行走的过程中至少保持生命值为1.
则dp[0][0] = max(1,1-dungeon[0][0])
若代表地牢的二维数组为1n或n1的数组:
1n,i从n-2至0:dp[0][i] = max(1,dp[0][i+1]-dungeon[0][i]);
n1,i从n-2至0:dp[i][0] = max(1,dp[i+1][0]-dungeon[i][0]);
若代表地牢的二维数组为n*m:
i代表行,从n-2至0:
j代表列,从n-2至0:
设dp_min = min(dp[i+1][j],dp[i][j+1])
dp[i][j] = max(1,dp_min - dungeon[i][j])
程序代码
public int calculateMinimumHP(int[][] dungeon) {
int row = dungeon.length;//行数
int col = dungeon[0].length;//列数
if(row == 0)return 1;//当网格为空,保证骑士健康的最小值为1
// 动态规划数组dp[i][j] 表示通过倒推到达原数组dungeon[i][j]位置时的最小血量
// 因此dp[0][0] 即为初始时的最小血量
int[][] dp = new int[row][col];
// 初始化
// 最后一个位置的最小血量为 健康点数1 - 进入最后一个位置dungeon[row-1][col-1]所消耗的血量(消耗最后一个位置前血量)
// 若倒推得最后一行消耗前血量<1,则说明消耗最后一个位置前血量最小值即为健康点数
dp[row-1][col-1] = max(1,1-dungeon[row-1][col-1]);
// 最后一行均由后一个位置向左递推
for(int i=col-2;i>=0;i--)dp[row-1][i] = max(1,dp[row-1][i+1] - dungeon[row-1][i]);
// 最后一列均由后一个位置向上递推
for(int i=row-2;i>=0;i--)dp[i][col-1] = max(1,dp[i+1][col-1] - dungeon[i][col-1]);
// 其余位置由下方位置或右方位置向上或者向左推得
for(int i=row-2;i>=0;i--)
for(int j=col-2;j>=0;j--) {
// 到达下方位置或者到达右方位置的最小生命值 中较小生命值
int min_dp = min(dp[i+1][j],dp[i][j+1]);
// 到达该位置的最小生命值 为到达下一个位置的较小生命值 - 该位置消耗的生命值
// 如果消耗该位置的生命值 < 0 ,则能保证到达该位置前的生命值为最小健康值即可。
dp[i][j] = max(1,min_dp - dungeon[i][j]);
}
return dp[0][0];//最初位置的值即为最初需要的最少生命值
}
public int min(int a,int b) {
return a>=b?b:a;
}
public int max(int a,int b) {
return a>=b?a:b;
}
剑指offer
例1:连续子数组的最大和(30)
题目描述
HZ偶尔会拿些专业问题来忽悠那些非计算机专业的同学。今天测试组开完会后,他又发话了:在古老的一维模式识别中,常常需要计算连续子向量的最大和,当向量全为正数的时候,问题很好解决。但是,如果向量中包含负数,是否应该包含某个负数,并期望旁边的正数会弥补它呢?例如:{6,-3,-2,7,-15,1,2,2},连续子向量的最大和为8(从第0个开始,到第3个为止)。给一个数组,返回它的最大连续子序列的和,你会不会被他忽悠住?(子向量的长度至少是1)
程序代码
// 30.连续子数组的最大和
// HZ偶尔会拿些专业问题来忽悠那些非计算机专业的同学。
// 今天测试组开完会后,他又发话了:在古老的一维模式识别中,常常需要计算连续子向量的最大和,
// 当向量全为正数的时候,问题很好解决。但是,如果向量中包含负数,是否应该包含某个负数,并期望旁边的正数会弥补它呢?
// 例如:{6,-3,-2,7,-15,1,2,2},连续子向量的最大和为8(从第0个开始,到第3个为止)。
// 给一个数组,返回它的最大连续子序列的和,你会不会被他忽悠住?(子向量的长度至少是1)
public int FindGreatestSumOfSubArray(int[] array) {
// 采用动态规划
// 设F(i) 表示以array[i]为结尾的子数组的最大值,则
// F(i) = max(F(i-1)+array[i],array[i]);
// 利用数组maxArray存储这些数组的最大值,则array中子数组最大值为maxValueOf(maxArray)
int[] maxArray = constructMaxSubArray(array);// maxArrays存储以array[i]为末尾的子数组的最大值
int maxSum = Integer.MIN_VALUE; // 记录子数组最大值
for(int i=0;imaxSum)maxSum = maxArray[i];
return maxSum;
}
// 自顶向下备忘录法
public int[] constructMaxSubArray(int[] array) {
int[] maxArray = new int[array.length];
maxArray[0] = array[0];
for(int i=1;i 例2:滑动窗口最大值(63)
题目描述
给定一个数组和滑动窗口的大小,找出所有滑动窗口里数值的最大值。例如,如果输入数组{2,3,4,2,6,2,5,1}及滑动窗口的大小3,那么一共存在6个滑动窗口,他们的最大值分别为{4,4,6,6,6,5}; 针对数组{2,3,4,2,6,2,5,1}的滑动窗口有以下6个: {[2,3,4],2,6,2,5,1}, {2,[3,4,2],6,2,5,1}, {2,3,[4,2,6],2,5,1}, {2,3,4,[2,6,2],5,1}, {2,3,4,2,[6,2,5],1}, {2,3,4,2,6,[2,5,1]}。
程序代码
// 63.滑动窗口的最大值
// 给定一个数组和滑动窗口的大小,找出所有滑动窗口里数值的最大值。
// 例如,如果输入数组{2,3,4,2,6,2,5,1}及滑动窗口的大小3,那么一共存在6个滑动窗口,他们的最大值分别为{4,4,6,6,6,5};
// 针对数组{2,3,4,2,6,2,5,1}的滑动窗口有以下6个:
// {[2,3,4],2,6,2,5,1}, {2,[3,4,2],6,2,5,1}, {2,3,[4,2,6],2,5,1},
// {2,3,4,[2,6,2],5,1}, {2,3,4,2,[6,2,5],1}, {2,3,4,2,6,[2,5,1]}。
ArrayList<Integer> maxInWindowsList = new ArrayList<Integer>(); // 窗口最大值列表
public ArrayList<Integer> maxInWindows(int [] num, int size)
{
if(size > num.length || size<=0)return maxInWindowsList;
getMaxWindowsList(num,size);
return maxInWindowsList;
}
public void getMaxWindowsList(int[] num,int size) {
// 填充窗口最大值列表的第 i 位置元素,即
// 以第 i+size-1 个元素作为窗口尾端元素时窗口的最大值
// 一共需要填充 num.length-size+1 个元素
// 以第 i 个元素为窗口尾端元素时窗口的最大值 = 上一个滑动窗口的最大值
// 初始化,窗口最大值列表
maxInWindowsList.add(findMaxInArray(num,0,size-1));
for(int i=1;i<num.length-size+1;i++) {
// 填充窗口最大值列表的第i个位置
// 为以 j 为末端的长为size的窗口最大值
// 若新添加数 num[j]> maxInWindowsList[i-1],则最大值为num[j]
// 否则,若最大值不为上一个滑动窗口的首元素,则最大值为maxInWindowsList[i-1]
// 否则,重新通过findMaxInArray遍历窗口元素寻找最大值
int j = i+size-1; // 滑动窗口最末端元素
int lastMax = maxInWindowsList.get(i-1);
if(num[j] > lastMax)maxInWindowsList.add(num[j]);
else {
if(num[i-1] != lastMax)maxInWindowsList.add(lastMax);
else maxInWindowsList.add(findMaxInArray(num,i,j));
}
}
}
2019校招真题
例1:牛牛找工作(1)
题目描述
为了找到自己满意的工作,牛牛收集了每种工作的难度和报酬。牛牛选工作的标准是在难度不超过自身能力值的情况下,牛牛选择报酬最高的工作。在牛牛选定了自己的工作后,牛牛的小伙伴们来找牛牛帮忙选工作,牛牛依然使用自己的标准来帮助小伙伴们。牛牛的小伙伴太多了,于是他只好把这个任务交给了你。
程序代码
// 1. 牛牛找工作
// // 方法1:贪心(超时)
// public class Work{ // 自定义工作类
// public int d; // 工作的难度
// public int p; // 工作的报酬
//
// public Work(int _d,int _p) {
// this.d = _d;
// this.p = _p;
// }
// }
//
// public class WorkComparator implements Comparator {
//
// @Override
// public int compare(Work w1, Work w2) { // 进行比较的工作
// if (w1.d > w2.d) { // 难度从小到大排序
// return 1;
// } else return -1;
// }
// }
//
// public void findWork() {
// // 输入
// Scanner sc = new Scanner(System.in);
// int n = sc.nextInt(); // 工作数量
// int m = sc.nextInt(); // 伙伴数量
// if(n==0 || m==0)return;
// ArrayList workList = new ArrayList(); // 工作列表
// ArrayList aOfFriendList = new ArrayList(); // 伙伴们能力列表
// for(int i=0;i
// int d = sc.nextInt();
// int p = sc.nextInt();
// workList.add(new Work(d,p));
// }
// for(int i=0;i
// int a = sc.nextInt();
// aOfFriendList.add(a);
// }
// helpFriendsFindWork(n,m,workList,aOfFriendList);
// }
//
// public void helpFriendsFindWork(int n,int m,ArrayList workList,ArrayList aOfFriendList) {
// // 对workList按照难度升序排序
// Collections.sort(workList, new WorkComparator());
// // 为每个伙伴寻找对应合适的工作
// for(int i=0;i
// Integer ability = aOfFriendList.get(i);
// Integer bestP = 0;
// for(int j=0;j
// if(ability >= workList.get(j).d) { // 能力值满足
// if(bestP < workList.get(j).p)bestP = workList.get(j).p;
// }else break;
// }
// System.out.println(bestP);
// }
// }
// 方法2:背包
// 背包思想:当前工作难度/能力值对应报酬 = max(低于该难度值工作对应最大报酬,已存在的该难度值对应的报酬)
// 找到难度不大于能力的所有工作里,报酬最多的。核心是用HashMap来记录难度和不超过该难度的最大报酬。
// 先把工作的难度和报酬映射到HashMap
// 把人的能力也全部读进来,放到HashMap,报酬可以先设为0.
// 最后按难度从小到大(所以需要先排序)更新HashMap,key为难度,value为不超过难度的最大报酬。
public void findWork() {
// 输入
Scanner sc = new Scanner(System.in);
int n = sc.nextInt(); // 工作数量
int m = sc.nextInt(); // 伙伴数量
if(n==0 || m==0)return;
int[] dList = new int[m+n]; // 对应工作能力/难度(记录所有工作能力)
int[] aList = new int[m]; // 伙伴对应工作能力
HashMap<Integer,Integer> pOfD = new HashMap<Integer,Integer>(); // 不超过该难度d所能得到的最大报酬p(d,p)
for(int i=0;i<n;i++) {
int d = sc.nextInt();
int p = sc.nextInt();
dList[i] = d;
pOfD.put(d, p);
}
for(int i=0;i<m;i++) {
int a = sc.nextInt();
dList[i+n] = a; // 将员工的工作能力加入数组
aList[i] = a;
if(!pOfD.containsKey(a))pOfD.put(a, 0); // 初始化员工能力对应的报酬为0
}
// 对工作难度升序排序
Arrays.sort(dList);
int maxP = 0;
for(int i=0;i<m+n;i++) {
// 由于工作难度升序排序,所以当前能力值对应的报酬为 max (maxP(小于该能力值所对应的最大报酬), dOfA(已存在该工作难度对应的报酬))
// 对HashMap进行更新
int d = dList[i];
maxP = Math.max(maxP, pOfD.get(d));
pOfD.replace(d, maxP);
}
for(int i=0;i<m;i++)
System.out.println(pOfD.get(aList[i]));
}
public static void main(String[] args) {
DP dp = new DP();
dp.findWork();
}
例2:牛牛的背包问题(8)
题目描述
牛牛准备参加学校组织的春游, 出发前牛牛准备往背包里装入一些零食, 牛牛的背包容量为w。
牛牛家里一共有n袋零食, 第i袋零食体积为v[i]。
牛牛想知道在总体积不超过背包容量的情况下,他一共有多少种零食放法(总体积为0也算一种放法)。
输入描述:
输入包括两行
第一行为两个正整数n和w(1 <= n <= 30, 1 <= w <= 2 * 10^9),表示零食的数量和背包的容量。
第二行n个正整数v[i](0 <= v[i] <= 10^9),表示每袋零食的体积。
输出描述:
输出一个正整数, 表示牛牛一共有多少种零食放法。
程序代码
// 8. 牛牛的背包问题
// 牛牛准备参加学校组织的春游, 出发前牛牛准备往背包里装入一些零食, 牛牛的背包容量为w。
// 牛牛家里一共有n袋零食, 第i袋零食体积为v[i]。
// 牛牛想知道在总体积不超过背包容量的情况下,他一共有多少种零食放法(总体积为0也算一种放法)。
Integer count = 0; // 零食放法
long[] v; // 零食体积列表
public void bagQuestion() {
// 典型背包问题:
// 基本思想:
// 1. 背包里共有n个位置,递归每个位置
// 2. 递归第 i 个位置,可选择放/不放零食,
// 3. 每个位置都有2个选择,一共需要递归 2^n 种可能。
// 遍历到最后一位置,如果容量
// 这种暴力穷举的算法,复杂度2^n,AC率为80%,考虑剪枝优化
// 思想2:
// 1. 若零食总体积<背包容量,说明所有零食均可放或者不可放,直接返回 2^n
// 2. 对零食体积列表进行排序,此时对于第 i 个位置
// 如果位置 i 处,加入第i个零食时容量已>w,则再加入后面的零食(更大的零食)一定不可行。此时后面的零食只有不放入的可能,因此直接count++,返回。
// 否则,则按思想1继续递归
Scanner sc = new Scanner(System.in);
int n = sc.nextInt(); // 零食的数量
long w = sc.nextLong(); // 背包的容量
v = new long[n];
long sum = 0;
for(int i=0;i<n;i++) {
v[i] = sc.nextLong();
sum += v[i];
}
if(sum <= w) {
System.out.println((int)Math.pow(2, n));
return;
}
Arrays.sort(v);
addSnackInBag(0,n,w,0);
System.out.println(count);
}
public void addSnackInBag(int i,int n,long w, long sum) {
// 在第 i 个位置放零食, sum 表示前 i-1 个位置零食所占容量
if(i == n && sum<=w) {count++;return;}
if(sum + v[i] <= w) {
addSnackInBag(i+1,n,w,sum+v[i]);
addSnackInBag(i+1,n,w,sum);
}else {
// addSnackInBag(i+1,n,w,sum);
count++;return;
}
}

