【新人学习渣作】渲染：从物体坐标系到世界坐标系

Shader"Custom/MyShader"{
        SubShader{
                  Pass{
                          #pragma vertex MyVertex
                          #pragma fragment MyFragment
                          #include "UnityCG.cginc"
                          struct VertexData
                          {
                                    float4 position:POSITION;
                                    float3 normal：NORMAL；
                              }
                              struct Interpolator{
                                     float4 position:SV_POSITION;
                                      float3 normal:TEXCOORD0;
                              }
                              Interpolator MyVertex（VertexData Data）
                              {
                                     Interpolator OutPut;
                                     OutPut.position = mul（UNITY_MATRIX_MVP,Data.position）;//投影到屏幕上
                                     OutPut.normal =  Data.normal;
                                     return Output;
                              }
                              float4 MyFragment（Interpolator input）:SV_TARGET
                              {
                                      return float4（input.normal*0.5 + 0.5，0）;
                              }
                  }
        }//屎一样的缩进格式

现在来测试一下着色器
完成后创建Material在场景中任意创建几个物体并任意平移，升缩，旋转变换后将material拖拽到物体上并将material的shader选项换为shader->Custom->MyShader。在场景中测试着色器效果。

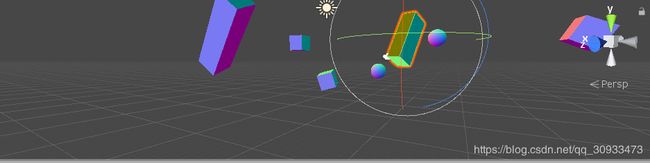
（懒得调相机位置就直接放上scence窗口的画面吧，懒狗本质）
可以发现物体的网格因为不同的法线方向渲染上了不同的颜色，旋转物体会发现物体每个网格的颜色不会随物体的位置变化而变化
此时在前文的VertexData中的

float3 normal:NORMAL;

在这里normal取得的是物体自己的坐标系中的法向量，而在场景中改变了物体的世界坐标并不会对normal的物体坐标系产生影响。如果想要让物体的颜色随着旋转变化的话就必须要取得物体的世界坐标系里的法线向量。
众所周知(大雾)在uniy中物体的坐标变换是通过矩阵乘法完成的（大一的噩梦线性代数）
世界坐标向量r 物体到世界变化矩阵Q 物体坐标向量o有
r = Q*o
而物体在世界坐标系下的变化是通过改变Transform组件中的位置(Position),旋转(Rotation),缩放(Scale)三个值实现的。其中物体的位置对物体的法线向量并无影响可以抛开不谈。对于旋转，和缩放
unity通过把rotation和scale的x,y,z值转换成相应的变换矩阵R0,R1…Rn和S1,S2…Sn后再与坐标相乘得到变换后的坐标的因此可以得到
r = R1R2…RnS1S2…Sno
同理我们可以学习unity的做法通过将得到的物体坐标系中的向量乘以在世界坐标系中的变化矩阵便可以得到在世界坐标系中的法向量了
在由UnityCG.cginc导入的文件UnityShaderVariables中定义了我们想要的变换矩阵Unity_ObjectToWorld于是我们对顶点程序这样处理:

Interpolator MyVertex（VertexData Data）
                  {
                         Interpolator OutPut;
                         OutPut.position = mul（UNITY_MATRIX_MVP,Data.position）;//投影到屏幕上
                         OutPut.normal =  mul(Unity_ObjectToWorld,Data.normal);//变换为世界坐标
                         OutPut.normal = normalize(Data.normal);
                         //考虑到Unity_ObjectToWorld中的Scale值的行列式不等于零会改变normal的向量模长
                         //这里用了normalize()函数将输出值规范化
                         return Output;
                  }

尽管如此，我们会发现这样处理的结果还是存在一些问题。
在变换时我们发现在Unity_ObjectToWorld中如果我们只是单纯的对某一平面进行单方向的缩放时
比如我们将A平面在x轴上做放大2倍，那么在渲染时我们取得了A的法向量a(x,y,z)后对它乘上Unity_ObjectToWorld进行变换我们会得到法向量a`(2x,y,z)
具体情况如下图：

这显然不是我们想要的
实际上我们期望的结果是：

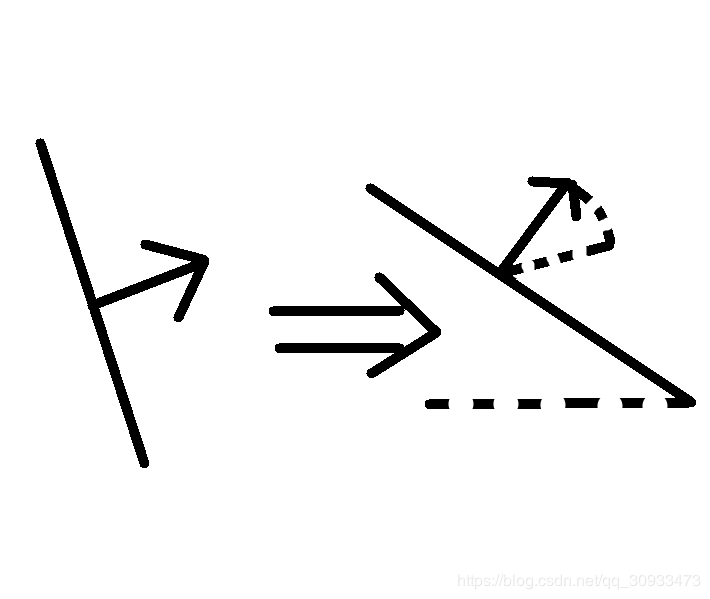
显然我们更想要这种效果
事实上我们会发现当平面在x轴方向上放大时，法向量在x轴方向的分量缩小了
对原法向量(x,y,z)平面上两个向量(x0,y0,z0)和(x1,y1,z1)有
xx0 + yy0 + zz0 = 0
xx1 + yy1 + zz1 = 0
然而当物体在x,y,z方向上放大a,b,c倍时两向量变为(ax0,by0,cz0)和(ax1,by1,cz1)
此时变化后的向量(X,Y,Z)应仍与这两个向量垂直于是有
aXx0 + bYy0 + cZz0 = 0
aXx1 + bYy1 + cZz1 = 0
由这几个方程我们观察不难得到
X = 1/ax Y = 1/by Z = 1/c*z
在对法线(x,y,z)处理时我们希望个方向上缩放为(1/a,1/b,1/c)
在unity的矩阵变换中我们希望找到这样的矩阵达到这种效果
而逆矩阵能满足这种要求
对一个矩阵A的逆矩阵A-1有
A A-1 = E
(关于A-1的求法找到矩阵(A E)将其进行有限次的简单变换后变成(E B)形式此时B = A-1)
对于缩放的变换矩阵如下当Scale的x =a ,y = b,z = c时
| a 0 0 |
| 0 b 0 |
| 0 0 c |
求逆后变换为
|1/a 0 0 |
| 0 1/b 0 |
| 0 0 1/c |
当这个逆矩阵做变换时可以达到我们上述的效果
unity也提供了这种逆矩阵Unity_WorldToObject
如果Unity_ObjectToWorld = S1S2S3…SnR1R2R3…RnP1P2P3…Pn的话
Unity_WorldToObject = P-1n …P-11R-1n…R-11S-1n…S-11(这里-1其实是上标。。。)
抛开对结果无影响的Pn不谈
我们期望的矩阵希望有旋转的正面效果也有缩放逆矩阵的效果也就是
Q = R1R2…RnS-11S-12…S-1n
因此我们要对Unity_WorldToObject继续处理
对一个矩阵旋转变换矩阵R有三个方向的旋转Rx,Ry,Rz
对Rx如果旋转值x为x0(设cosx0为C,sinx0为S)
那么旋转矩阵Rx为
| C S 0 |
| -S C 0 |
| 0 0 1 |
Rx的逆矩阵R-1x为
| C -S 0 |
| S C 0 |
| 0 0 1 |
可以发现R-1x的数据相比Rx除了沿对角线交换之外没有别的变化
以对角线为对称轴将对角线的两边的数字交换的变换为矩阵的转置如：
对矩阵A
| a0 a1 a2|
| b0 b1 b2|
| c0 c1 c2|
A的转置AT为
| a0 b0 c0|
| a1 b1 c1|
| a2 b2 c2|
那么对Rx的逆矩阵R-1x转置(R-1x)T=
| C S 0 |
| -S C 0 | = Rx
| 0 0 1 |
对Sx的逆矩阵S-1x转置(S-1x)T =
| 1/x 0 0 |
| 0 1/y 0 | = S-1x
| 0 0 1/z|
我们可以得到
(R-1x)T = Rx (S-1x)T = S-1x
现在我们希望得到变化矩阵
Q = R1R2…RnS-11S-12…S-1n
如果哦我们对Unity_WorldToObject矩阵(下文简称UWO)转置的话我们会发现
(UWO)T = (R-11R-12…R-1nS-11S-12…S-1n)T= S-1n…S-11Rn…R1 = Q
也就是说Unity_WorldToObject的转置矩阵就是我们需要的矩阵
在Unity中定义了transpose函数来进行矩阵的转置操作
于是我们可以改写MyVertex函数

Interpolator MyVertex（VertexData Data）
                  {
                         Interpolator OutPut;
                         OutPut.position = mul（UNITY_MATRIX_MVP,Data.position）;//投影到屏幕上
                         //OutPut.normal =  mul(Unity_ObjectToWorld,Data.normal);//变换为世界坐标
                         //下面是新版变化
                         OutPut.normal = mul(transpose(Unity_WorldToObject),Data.normal);
                         OutPut.normal = normalize(Data.normal)；
                         return Output;
                  }

注意要在MyFragment函数中也对片段进行标准化

 float4 MyFragment（Interpolator input）:SV_TARGET
                   {
                            float4 result = float4(input.normal*0.5+0.5,0);
                            result = normalize(result);
                            return result;
                   }

最后放到场景里测试一下

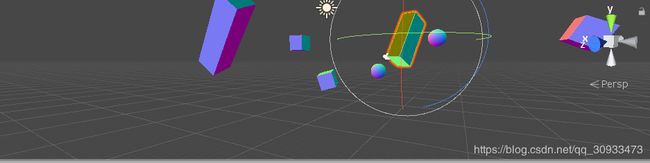
发现物体表面的颜色会随着选转发生变化
也就是说这个时候normal取得的发向量随着物体的变换发生了变化
当然如果你想省事的话，Unity内置了方法UnityObjectToWorldNormal可以满足以上的要求

Interpolator MyVertex（VertexData Data）
                  {
                         Interpolator OutPut;
                         OutPut.position = mul（UNITY_MATRIX_MVP,Data.position）;
                         OutPut.normal = UnityObjectToWorldNormal(Data.normal);
                         OutPut.normal = normalize(Data.normal)；
                         return Output;
                  }

不需要之前的数学知识也能取得之前的效果
【unity刚开始学习的新手，有问题还请大佬指正】