by jie 2018.7
一. g2o的整体结构
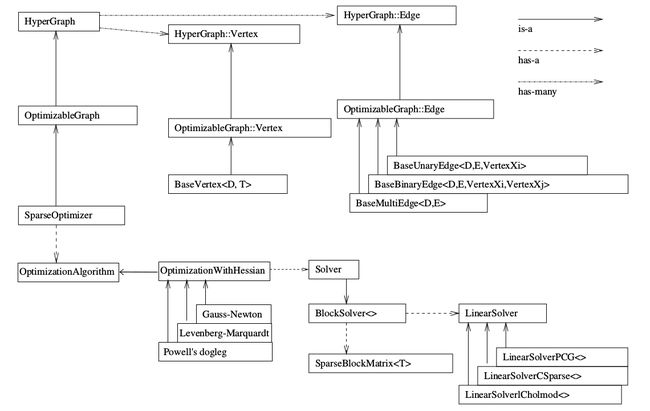
说到整体的结构,不得不用一张比较概括的图来说明:
这张图最好跟着画一下,这样能更好的理解和掌握,例如我第一次看的时候根本没有注意说箭头的类型等等的细节。
先看上半部分。SparseOptimizer 是我们最终要维护的东东。它是一个Optimizable Graph,从而也是一个Hyper Graph。一个 SparseOptimizer 含有很多个顶点 (都继承自 Base Vertex)和很多个边(继承自 BaseUnaryEdge, BaseBinaryEdge或BaseMultiEdge)。这些 Base Vertex 和 Base Edge 都是抽象的基类,而实际用的顶点和边,都是它们的派生类。我们用 SparseOptimizer.addVertex 和 SparseOptimizer.addEdge 向一个图中添加顶点和边,最后调用 SparseOptimizer.optimize 完成优化。
在优化之前,需要指定我们用的求解器和迭代算法。从图中下半部分可以看到,一个 SparseOptimizer 拥有一个 Optimization Algorithm,继承自Gauss-Newton, Levernberg-Marquardt, Powell's dogleg 三者之一(我们常用的是GN或LM)。同时,这个 Optimization Algorithm 拥有一个Solver,它含有两个部分。一个是 SparseBlockMatrix ,用于计算稀疏的雅可比和海塞; 一个是用于计算迭代过程中最关键的一步 见书p111
HΔx=−b
这就需要一个线性方程的求解器。而这个求解器,可以从 PCG, CSparse, Choldmod 三者选一。
综上所述,在g2o中选择优化方法一共需要三个步骤:
- 选择一个线性方程求解器,从 PCG, CSparse, Choldmod中选,实际则来自 g2o/solvers 文件夹中定义的东东。
- 选择一个 BlockSolver 。
- 选择一个迭代策略,从GN, LM, Doglog中选。
那么从图中我们其实比较容易的就看出来整个库里面较为重要的类之间的继承以及包含关系,也可以看出整个框架里面最重要的东西就是SparseOptimizer这个类(或者说实例)。
顶点(Vertex)和边(Edge)
顺着图往上看,可以看到我们所使用的优化器最终是一个超图(hyperGrahp),而这个超图包含了许多顶点(Vertex)和边(Edge)。这两个类型是我们在看程序和写程序中比较关注的东西了,g2o不像Ceres,内部很多东西其实作者都已经写好了,但是同时,我们也失去了一个比较完整的了解内部关系的机会,不过这个东西我们可以通过看内部的实现补回来。
在图优化中,顶点代表了要被优化的变量,而边则是连接被优化变量的桥梁,因此,也就造成了说我们在程序中见得较多的就是这两种类型的初始化和赋值。
在整个优化过程中,顶点的值会越来越趋近于最优值,优化完毕后则可以将顶点的优化值作为最优值进行使用;边则是连接顶点的类型,在SLAM问题中,一般是边连接要被优化的空间点(Point)和机器人的位姿(Pose),当然,边还可以连接一个顶点(类似与参数估计,边的数量由量测的数量决定),也可以连接多个顶点(超图),边在图优化中的一个很大的作用就是计算误差(视觉SLAM中计算的就是空间点的映射误差),同时计算该误差对于被优化变量的jacobian矩阵,也是比较重要的存在。
1.1 自定义顶点(Vertex)和边(Edge)
我们在用g2o的时候,不会一帆风顺的就能适合自身机器人的实际情况,总会遇到自己独特的顶点类型和边类型,此时我们需要对顶点和边进行重写,那么重写也比较简单,这里简单进行记录。
在整体框架图中,可以看到不管是顶点还是边,都可以说是继承自baseXXX这个类的,因此我们在自定义的时候,也可以仿照着继承这两个类,当然也可以继承自g2o中较为“成熟”的类,不管怎样,都要重写下述的函数。
自定义顶点
virtual bool read(std::istream& is);
virtual bool write(std::ostream& os) const;
virtual void oplusImpl(const number_t* update);
virtual void setToOriginImpl();
其中read,write函数可以不进行覆写,仅仅声明一下就可以,setToOriginImpl设定被优化变量的原始值,oplusImpl比较重要,我们根据增量方程计算出增量之后,就是通过这个函数对估计值进行调整的,因此这个函数的内容一定要写对,否则会造成一直优化却得不到好的优化结果的现象。
自定义边
virtual bool read(std::istream& is);
virtual bool write(std::ostream& os) const;
virtual void computeError();
virtual void linearizeOplus();
read和write函数同上,computeError函数是使用当前顶点的值计算的测量值与真实的测量值之间的误差,linearizeOplus函数是在当前顶点的值下,该误差对优化变量的偏导数,即jacobian。
注意:如果没有定义边的linearizeOplus函数,就会调用数值求导,运算比较慢。
总结
不管是自定义边还是顶点,除了自己加入的一些变量,还都要对一些g2o框架要调用的函数进行覆写,这些函数用户可以声明为实函数(即不加virtual),但是笔者还是建议声明为虚函数。
1.2 优化算法
顺着整体结构图往下看,可以看到这部分其实算是整个g2o里面比较隐晦的部分,设计到优化的算法,块求解器,线性求解器等等部分,在程序中,这部分通常位于g2o算法的开头配置部分,一般情况下我们可以随着一个例程进行配置即可,这里对这部分进行了稍微浅显的理解。
我们知道在求解增量方程HdeltaX=-b的时候,通常情况下想到线性求解,很简单嘛,deltaX=-H.inv*b,的确,当H的维度较小的时候,上述问题变得简单,只需要矩阵的求逆就能解决问题,但是当H的维度较大时,问题变得复杂,此时我们就需要一些特殊的方法对矩阵进行求逆,g2o中主要有图中所示的三种方法,PCG,CSparse和Cholmod方法。
注意,这里说再多,线性求解器仅仅只是完成了一个求解的功能,可以说是整个优化中比较靠后的计算部分了。
BlockSolver:块求解器(参数块求解器?)
块求解器是包含线性求解器的存在,之所以是包含,是因为块求解器会构建好线性求解器所需要的矩阵块(也就是H和b),之后给线性求解器让它进行运算,边的jacobian也就是在这个时候发挥了自己的光和热。
这里再记录下一个比较容易混淆的问题,也就是在初始化块求解器的时候的参数问题。
大部分的例程在初始化块求解器的时候都会使用如下的程序代码:
std::unique_ptr linearSolver =
g2o::make_unique>();
其中的BlockSolver_6_3有两个参数,分别是6和3,在定义的时候可以看到这是一个模板的重命名(模板类的重命名只能用using)
template
using BlockSolverPL = BlockSolver< BlockSolverTraits >;
其中p代表pose的维度,l表示landmark的维度,且这里都表示的是增量的维度(这里笔者也不是很确定,但是从后续的程序中可以看出是增量的维度而并非是状态变量的维度)。
因此(后面的话以SLAM情况为例),对于仅仅优化位姿的应用而言,这里l的值是没有太大影响的,因为H矩阵中并没有Hll的块,因此这里的维度也就没有用武之地了。
优化算法
从图中可以看到主要有三种方法:GN,LM,PSD,不同的方法主要表现在最终的H矩阵构造不同。
1.3 SLAM使用g2o过程
使用g2o来实现图优化还是比较容易的。它帮你把节点和边的类型都定义好了,基本上只需使用它内置的类型而不需自己重新定义。要构造一个图,要做以下几件事:
定义一个SparseOptimizer. 编写方式参见tutorial_slam2d的声明方式。你还要写明它使用的算法。通常是Gauss-Newton或LM算法。个人觉得后者更好一些。
定义你要用到的边、节点的类型。例如我们实现一个3D SLAM。那么就要看它的g2o/types/slam3d下面的头文件。节点头文件都以vertex_开头,而边则以edge_开头。在我们上面的模型中,可以选择vertex_se3作为节点,edge_se3作为边。这两个类型的节点和边的数据都可以直接来自于Eigen::Isometry,即上面讲到过的变换矩阵T。
编写一个帧间匹配程序,通过两张图像算出变换矩阵。这个用opencv, pcl都可以做。
把你得到的关键帧作为节点,变换矩阵作为边,加入到optimizer中。同时设定节点的估计值(如果没有惯性测量就设成零)与边的约束(变换矩阵)。此外,每条边还需设定一个信息矩阵(协方差矩阵之逆)作为不确定性的度量。 例如你觉得帧间匹配精度在0.1m,那么把信息矩阵设成100的对角阵即可。
在程序运行过程中不断作帧间检测,维护你的图。
程序结束时调用optimizer.optimize( steps )进行优化。优化完毕后读取每个节点的估计值,此时就是优化后的机器人轨迹。
参考:视觉SLAM漫谈(二):图优化理论与g2o的使用
二. 详解g2o的顶点和边
参考:g2o学习-再看顶点和边
跟着g2o的slam2d_tutorial进行了学习,发现自己对于顶点和边的理解还是不太够,觉得有必要把顶点和边的一些东西再给总结一下,主要参考的就是如下网站: 函数api
这个网站里面有较为全面的g2o的类以及函数的讲解,很方便。
2.1 g2o的顶点vertex
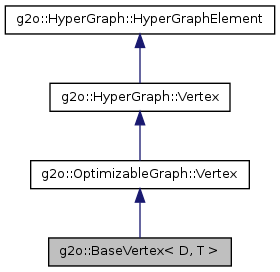
首先我们来看一下顶点的继承关系:
可以看到比较“成熟”的类型就是BaseVertex了,由于我们一般在派生的时候就是继承自这个类的,下面主要是对这个类进行分析,其中个人认为还是有很多东西要注意的。
g2o::BaseVrtex< D, T >
int D, typename T
首先记录一下定义模板的两个参数D和T,两个类型分别是int和typename的类型,D表示的是维度,g2o源码里面是这个注释的
static const int Dimension = D; ///< dimension of the estimate (minimal) in the manifold space
可以看到这个D并非是顶点(更确切的说是状态变量)的维度,而是其在流形空间(manifold)的最小表示,这里一定要区别开;之后是T,源码里面也给出了T的作用
typedef T EstimateType;
EstimateType _estimate;
可以看到,这里T就是顶点(状态变量)的类型。
在顶点的继承中,这两个参数是直接面向我们的,所以务必要定义妥当。
hessian矩阵和b向量
增量方程很重要的就是H和b两个参数,这里的_hessian和_b是增量方程中H和b的一部分,更确切的说是对应于该顶点的部分,下面简单的说一下这两个参数的作用。
_hessian矩阵
它的类型是Eigen中的Map类型,也就是这个参数只是一个映射,把一块内存区域映射为Eigen中的数据类型,具体这里就不赘述了。它的作用也比较简单,就是拿到边中算出的jacobian,之后根据公式H=JTWJ计算出整个大H中该处理的数据。
相关的程序代码这里:
block_solver.hpp
_b矩阵
它的类型就是简单的Eigen::Vector,这里不是用的映射关系,但是他的作用和上述的类似,只不过最后是通过拷贝把b=JTerror给整个的b。
相关代码如下:
virtual int copyB(number_t* b_) const {
memcpy(b_, _b.data(), Dimension * sizeof(number_t));
return Dimension;
}
2.2 g2o的边(Edge)
首先我们也是先给出边的继承关系
g2o二元边的继承关系
这里截取的是二元边的继承图,下面的分析也是以该二元边为例的。
g2o::BaseBinaryEdge< D, E, VertexXi, VertexXj >
int D, typename E
首先还是介绍这两个参数,还是从源码上来看
static const int Dimension = D;
typedef E Measurement;
typedef Eigen::Matrix ErrorVector;
可以看到,D决定了误差的维度,从映射的角度讲,三维情况下就是2维的,二维的情况下是1维的;然后E是measurement的类型,也就是测量值是什么类型的,这里E就是什么类型的(一般都是Eigen::VectorN表示的,N是自然数)。和前面一样,这两个参数是直接面向我们的,一定要定义妥当。
typename VertexXi, typename VertexXj
这两个参数就是边连接的两个顶点的类型,这里特别注意一下,这两个必须一定是顶点的类型,也就是继承自BaseVertex等基础类的类!不是顶点的数据类!例如必须是VertexSE3Expmap而不是VertexSE3Expmap的数据类型类SE3Quat。原因的话源码里面也很清楚,因为后面会用到一系列顶点的维度等等的属性,这些属性是数据类型类里面没有的。
总结
- 在定义自己的边和顶点的时候,务必要弄明白D和E所代表的含义,在定义边的时候还要注意后面两个参数一定是一个顶点的类而不是数据类型;
- 在边的linearizeOplus函数定义时,如果我们有更简洁的数学表达,那么可以转化为编程语言进行求解,如果没有,也可以使用父类的求解方法,但是这种方法由于使用了循环,甚至中间还求了多次映射误差,因此较为耗时;
- 千万不要以为g2o会帮你区分什么是pose,什么是point,从而对号入座在Hpp和Hll中,这块必须由用户设定marginalization告诉g2o什么顶点归在那一块里面;
- 综合看来,g2o帮助我们实现了很多内部的算法,但是在进行构造的时候,也需要遵循一些规则。
三. 求解器
参考:g2o学习——顶点和边之外的solver
3.1 块求解器(BlockSolver_P_L)
首先祭出他的源码:
template
using BlockSolverPL = BlockSolver< BlockSolverTraits >;
接着往上走,我们会看到比较详细的BlockSoverTraits类
template
struct BlockSolverTraits
{
static const int PoseDim = _PoseDim;
static const int LandmarkDim = _LandmarkDim;
typedef Eigen::Matrix PoseMatrixType;
typedef Eigen::Matrix LandmarkMatrixType;
typedef Eigen::Matrix PoseLandmarkMatrixType;
typedef Eigen::Matrix PoseVectorType;
typedef Eigen::Matrix LandmarkVectorType;
typedef SparseBlockMatrix PoseHessianType;
typedef SparseBlockMatrix LandmarkHessianType;
typedef SparseBlockMatrix PoseLandmarkHessianType;
typedef LinearSolver LinearSolverType;
};
/**
* \brief traits to summarize the properties of the dynamic size optimization problem
*/
template <>
struct BlockSolverTraits
{
static const int PoseDim = Eigen::Dynamic;
static const int LandmarkDim = Eigen::Dynamic;
typedef MatrixX PoseMatrixType;
typedef MatrixX LandmarkMatrixType;
typedef MatrixX PoseLandmarkMatrixType;
typedef VectorX PoseVectorType;
typedef VectorX LandmarkVectorType;
typedef SparseBlockMatrix PoseHessianType;
typedef SparseBlockMatrix LandmarkHessianType;
typedef SparseBlockMatrix PoseLandmarkHessianType;
typedef LinearSolver LinearSolverType;
};
接着是比较详细的BlockSolver类
template
class BlockSolver: public BlockSolverBase
{
public:
static const int PoseDim = Traits::PoseDim;
static const int LandmarkDim = Traits::LandmarkDim;
typedef typename Traits::PoseMatrixType PoseMatrixType;
typedef typename Traits::LandmarkMatrixType LandmarkMatrixType;
typedef typename Traits::PoseLandmarkMatrixType PoseLandmarkMatrixType;
typedef typename Traits::PoseVectorType PoseVectorType;
typedef typename Traits::LandmarkVectorType LandmarkVectorType;
typedef typename Traits::PoseHessianType PoseHessianType;
typedef typename Traits::LandmarkHessianType LandmarkHessianType;
typedef typename Traits::PoseLandmarkHessianType PoseLandmarkHessianType;
typedef typename Traits::LinearSolverType LinearSolverType;
public:
/**
* allocate a block solver ontop of the underlying linear solver.
* NOTE: The BlockSolver assumes exclusive access to the linear solver and will therefore free the pointer
* in its destructor.
*/
BlockSolver(std::unique_ptr linearSolver);
~BlockSolver();
virtual bool init(SparseOptimizer* optmizer, bool online = false);
virtual bool buildStructure(bool zeroBlocks = false);
virtual bool updateStructure(const std::vector& vset, const HyperGraph::EdgeSet& edges);
virtual bool buildSystem();
virtual bool solve();
virtual bool computeMarginals(SparseBlockMatrix& spinv, const std::vector >& blockIndices);
virtual bool setLambda(number_t lambda, bool backup = false);
virtual void restoreDiagonal();
virtual bool supportsSchur() {return true;}
virtual bool schur() { return _doSchur;}
virtual void setSchur(bool s) { _doSchur = s;}
LinearSolver& linearSolver() const { return *_linearSolver;}
virtual void setWriteDebug(bool writeDebug);
virtual bool writeDebug() const {return _linearSolver->writeDebug();}
virtual bool saveHessian(const std::string& fileName) const;
virtual void multiplyHessian(number_t* dest, const number_t* src) const { _Hpp->multiplySymmetricUpperTriangle(dest, src);}
protected:
void resize(int* blockPoseIndices, int numPoseBlocks,
int* blockLandmarkIndices, int numLandmarkBlocks, int totalDim);
void deallocate();
std::unique_ptr> _Hpp;
std::unique_ptr> _Hll;
std::unique_ptr> _Hpl;
std::unique_ptr> _Hschur;
std::unique_ptr> _DInvSchur;
std::unique_ptr> _HplCCS;
std::unique_ptr> _HschurTransposedCCS;
std::unique_ptr _linearSolver;
std::vector > _diagonalBackupPose;
std::vector > _diagonalBackupLandmark;
# ifdef G2O_OPENMP
std::vector _coefficientsMutex;
# endif
bool _doSchur;
std::unique_ptr> _coefficients;
std::unique_ptr> _bschur;
int _numPoses, _numLandmarks;
int _sizePoses, _sizeLandmarks;
};
那么有了以上的信息,整个BlockSolver_P_L的作用也就比较清楚了,还是那句老话:P表示的是Pose的维度(注意一定是流形manifold下的最小表示),L表示Landmark的维度(这里就不涉及流行什么事儿了)。这里思考一个问题,假如说在某个应用下,我们的P和L在程序开始并不能确定(例如程序中既有映射关系的边,同时还有位姿图之间的边,这时候的Hpp矩阵将不是那么的稀疏),那么此时这个块状求解器如何定义呢?其实也比较简单,g2o已经帮我们定义了一个不定的BlockSolverTraits,所有的参数都在中间过程中被确定,那么为什么g2o还帮助我们定义了一些常用的类型呢?一种可能是出于节约初始化时间的角度出发的,但是个人估计不是很靠谱,毕竟C++申请出一块内存应该还是很快的,没有必要为了这点儿时间纠结;那么另一种也许就是作者想把常用的类型定义出来而已吧~
3.2 优化器(optimizer)和初始化(initializeOptimization)
想必这句话大家应该也经常用到
optimizer.initializeOptimization();
这个函数里面都干了什么:
- 把所有的顶点(Vertex)插入到vset的集合中(set不用担心插入了相同的顶点)
- 遍历vset集合,取出每个顶点的边(这里每个边都有一个level的概念,默认情况下,g2o只处理level=0的边,在orbslam中,如果确定某个边的重投影误差过大,则把level设置为1,也就是舍弃这个边对于整个优化的影响),并判断边所连接的顶点是否都是有效的(在vset中),如果是,则认为这是一个有效的边和顶点,并分别加入到_activeEdges和_activeVertices中(妈妈在也不用担心边少顶点或者图中没有边的顶点了)
- 对上述的_activeEdges和_activeVertices按照ID号进行排序,其中Vertex的ID号是自己设置的,而Edge的ID号是g2o内部有个变量进行赋值的
- 对于上述的_activeVertices,剔除掉固定点(fixed)之后,把所有的顶点按照不被margin 在前,被margin在后的顺序排成vector类型,变量为_ivMap,这个变量很重要,基本上后面的所有程序都是用这个变量进行遍历的
以上就是初始化过程的全部,具体的代码如下:
bool SparseOptimizer::initializeOptimization(HyperGraph::VertexSet& vset, int level){
if (edges().size() == 0) {
cerr << __PRETTY_FUNCTION__ << ": Attempt to initialize an empty graph" << endl;
return false;
}
preIteration(-1);
bool workspaceAllocated = _jacobianWorkspace.allocate(); (void) workspaceAllocated;
assert(workspaceAllocated && "Error while allocating memory for the Jacobians");
clearIndexMapping();
_activeVertices.clear();
_activeVertices.reserve(vset.size());
_activeEdges.clear();
set auxEdgeSet; // temporary structure to avoid duplicates
for (HyperGraph::VertexSet::iterator it=vset.begin(); it!=vset.end(); ++it){
OptimizableGraph::Vertex* v= (OptimizableGraph::Vertex*) *it;
const OptimizableGraph::EdgeSet& vEdges=v->edges();
// count if there are edges in that level. If not remove from the pool
int levelEdges=0;
for (OptimizableGraph::EdgeSet::const_iterator it=vEdges.begin(); it!=vEdges.end(); ++it){
OptimizableGraph::Edge* e=reinterpret_cast(*it);
if (level < 0 || e->level() == level) {
bool allVerticesOK = true;
for (vector::const_iterator vit = e->vertices().begin(); vit != e->vertices().end(); ++vit) {
if (vset.find(*vit) == vset.end()) {
allVerticesOK = false;
break;
}
}
if (allVerticesOK && !e->allVerticesFixed()) {
auxEdgeSet.insert(e);
levelEdges++;
}
}
}
if (levelEdges){
_activeVertices.push_back(v);
// test for NANs in the current estimate if we are debugging
# ifndef NDEBUG
int estimateDim = v->estimateDimension();
if (estimateDim > 0) {
VectorX estimateData(estimateDim);
if (v->getEstimateData(estimateData.data()) == true) {
int k;
bool hasNan = arrayHasNaN(estimateData.data(), estimateDim, &k);
if (hasNan)
cerr << __PRETTY_FUNCTION__ << ": Vertex " << v->id() << " contains a nan entry at index " << k << endl;
}
}
# endif
}
}
_activeEdges.reserve(auxEdgeSet.size());
for (set::iterator it = auxEdgeSet.begin(); it != auxEdgeSet.end(); ++it)
_activeEdges.push_back(*it);
sortVectorContainers();
bool indexMappingStatus = buildIndexMapping(_activeVertices);
postIteration(-1);
return indexMappingStatus;
}
3.3 优化器(Optimizer)的优化(optimize)
初始化之后,我们基本上就可以调用optimize函数进行图优化了,如果只看optimize函数的代码,十分简单,首先判断_ivMap是否为空,之后直接调用_algorithm的solve函数,最后打印一些信息,之后循环一定的次数,此时就大功告成。所以下面的内容主要是围绕着_algorithm的solve函数进行。
算法(algorithm)的solve函数
在第一次进行迭代的时候,g2o要对整个矩阵块进行初始化,主要依靠块求解器的buildStructure()函数进行,那么想必大家也知道了,既然在块求解器中,那么必然就是对要用的矩阵块进行初始化,确实如此,我们稍微对这个函数进行展开:
(1) 对_ivMap进行遍历,如果顶点的margin标志为false,则认为是Pose,否则,认为是Landmark,所以在使用g2o的时候千万要注意,不要想当然的认为g2o会帮助我们区分Pose和Landmark
(2) 构建期待已久的Hpp,Hll等矩阵,每个矩阵的类型都是SparseBlockMatrix类型的
(3) 开始对应环节,这个过程首先是遍历_ivMap,将Hpp和Hll中对应于该顶点的矩阵块映射到顶点内部的_hessian矩阵中,这步的作用在我的上个博客中已经讲过了,感兴趣的可以看g2o学习——再看顶点和边,之后开始遍历所有的边,取出边的两个顶点,如果两个顶点都不margin的话,则在把Hpp中的两个顶点相交的地方的内存映射给边的内部_hessian矩阵;如果两个中一个margin一个不margin的话,则把Hpl中相交的地方的内存映射给边的_hessian矩阵;如果两个都margin的话,则把Hll中相交的地方的内存映射给边的_hessian矩阵
(4) 映射完成之后,如果我们使用schur消元的话,还要构建一个schur消元的中间矩阵,_Hschur,这个地方比较复杂,这里不做展开,对照公式看源码就可以,源码如下:
template
bool BlockSolver::buildStructure(bool zeroBlocks)
{
assert(_optimizer);
size_t sparseDim = 0;
_numPoses=0;
_numLandmarks=0;
_sizePoses=0;
_sizeLandmarks=0;
int* blockPoseIndices = new int[_optimizer->indexMapping().size()];
int* blockLandmarkIndices = new int[_optimizer->indexMapping().size()];
for (size_t i = 0; i < _optimizer->indexMapping().size(); ++i) {
OptimizableGraph::Vertex* v = _optimizer->indexMapping()[i];
int dim = v->dimension();
if (! v->marginalized()){
v->setColInHessian(_sizePoses);
_sizePoses+=dim;
blockPoseIndices[_numPoses]=_sizePoses;
++_numPoses;
} else {
v->setColInHessian(_sizeLandmarks);
_sizeLandmarks+=dim;
blockLandmarkIndices[_numLandmarks]=_sizeLandmarks;
++_numLandmarks;
}
sparseDim += dim;
}
resize(blockPoseIndices, _numPoses, blockLandmarkIndices, _numLandmarks, sparseDim);
delete[] blockLandmarkIndices;
delete[] blockPoseIndices;
// allocate the diagonal on Hpp and Hll
int poseIdx = 0;
int landmarkIdx = 0;
for (size_t i = 0; i < _optimizer->indexMapping().size(); ++i) {
OptimizableGraph::Vertex* v = _optimizer->indexMapping()[i];
if (! v->marginalized()){
//assert(poseIdx == v->hessianIndex());
PoseMatrixType* m = _Hpp->block(poseIdx, poseIdx, true);
if (zeroBlocks)
m->setZero();
v->mapHessianMemory(m->data());
++poseIdx;
} else {
LandmarkMatrixType* m = _Hll->block(landmarkIdx, landmarkIdx, true);
if (zeroBlocks)
m->setZero();
v->mapHessianMemory(m->data());
++landmarkIdx;
}
}
assert(poseIdx == _numPoses && landmarkIdx == _numLandmarks);
// temporary structures for building the pattern of the Schur complement
SparseBlockMatrixHashMap* schurMatrixLookup = 0;
if (_doSchur) {
schurMatrixLookup = new SparseBlockMatrixHashMap(_Hschur->rowBlockIndices(), _Hschur->colBlockIndices());
schurMatrixLookup->blockCols().resize(_Hschur->blockCols().size());
}
// here we assume that the landmark indices start after the pose ones
// create the structure in Hpp, Hll and in Hpl
for (SparseOptimizer::EdgeContainer::const_iterator it=_optimizer->activeEdges().begin(); it!=_optimizer->activeEdges().end(); ++it){
OptimizableGraph::Edge* e = *it;
for (size_t viIdx = 0; viIdx < e->vertices().size(); ++viIdx) {
OptimizableGraph::Vertex* v1 = (OptimizableGraph::Vertex*) e->vertex(viIdx);
int ind1 = v1->hessianIndex();
if (ind1 == -1)
continue;
int indexV1Bak = ind1;
for (size_t vjIdx = viIdx + 1; vjIdx < e->vertices().size(); ++vjIdx) {
OptimizableGraph::Vertex* v2 = (OptimizableGraph::Vertex*) e->vertex(vjIdx);
int ind2 = v2->hessianIndex();
if (ind2 == -1)
continue;
ind1 = indexV1Bak;
bool transposedBlock = ind1 > ind2;
if (transposedBlock){ // make sure, we allocate the upper triangle block
std::swap(ind1, ind2);
}
if (! v1->marginalized() && !v2->marginalized()){
PoseMatrixType* m = _Hpp->block(ind1, ind2, true);
if (zeroBlocks)
m->setZero();
e->mapHessianMemory(m->data(), viIdx, vjIdx, transposedBlock);
if (_Hschur) {// assume this is only needed in case we solve with the schur complement
schurMatrixLookup->addBlock(ind1, ind2);
}
} else if (v1->marginalized() && v2->marginalized()){
// RAINER hmm.... should we ever reach this here????
LandmarkMatrixType* m = _Hll->block(ind1-_numPoses, ind2-_numPoses, true);
if (zeroBlocks)
m->setZero();
e->mapHessianMemory(m->data(), viIdx, vjIdx, false);
} else {
if (v1->marginalized()){
PoseLandmarkMatrixType* m = _Hpl->block(v2->hessianIndex(),v1->hessianIndex()-_numPoses, true);
if (zeroBlocks)
m->setZero();
e->mapHessianMemory(m->data(), viIdx, vjIdx, true); // transpose the block before writing to it
} else {
PoseLandmarkMatrixType* m = _Hpl->block(v1->hessianIndex(),v2->hessianIndex()-_numPoses, true);
if (zeroBlocks)
m->setZero();
e->mapHessianMemory(m->data(), viIdx, vjIdx, false); // directly the block
}
}
}
}
}
if (! _doSchur) {
delete schurMatrixLookup;
return true;
}
_DInvSchur->diagonal().resize(landmarkIdx);
_Hpl->fillSparseBlockMatrixCCS(*_HplCCS);
for (OptimizableGraph::Vertex* v : _optimizer->indexMapping()) {
if (v->marginalized()){
const HyperGraph::EdgeSet& vedges=v->edges();
for (HyperGraph::EdgeSet::const_iterator it1=vedges.begin(); it1!=vedges.end(); ++it1){
for (size_t i=0; i<(*it1)->vertices().size(); ++i)
{
OptimizableGraph::Vertex* v1= (OptimizableGraph::Vertex*) (*it1)->vertex(i);
if (v1->hessianIndex()==-1 || v1==v)
continue;
for (HyperGraph::EdgeSet::const_iterator it2=vedges.begin(); it2!=vedges.end(); ++it2){
for (size_t j=0; j<(*it2)->vertices().size(); ++j)
{
OptimizableGraph::Vertex* v2= (OptimizableGraph::Vertex*) (*it2)->vertex(j);
if (v2->hessianIndex()==-1 || v2==v)
continue;
int i1=v1->hessianIndex();
int i2=v2->hessianIndex();
if (i1<=i2) {
schurMatrixLookup->addBlock(i1, i2);
}
}
}
}
}
}
}
_Hschur->takePatternFromHash(*schurMatrixLookup);
delete schurMatrixLookup;
_Hschur->fillSparseBlockMatrixCCSTransposed(*_HschurTransposedCCS);
return true;
}
上述块矩阵以及映射关系对应好以后,接下来比较重要的函数就是solver的buildSystem函数,这个函数的主要功能就是将增量方程(HΔx=−b)中的H矩阵和b向量赋予该有的值,具体过程如下:
(1) 遍历所有的边,计算该边误差所产生的jacobian矩阵
(2)根据公式H=JTWJ计算每个顶点的_hessian矩阵,b=JTWδ计算b向量,如果该边是个二元边,且两个定点都没有被fix的时候,还会根据H=JT1WJ计算相交部分的_hessian矩阵。
(3)由于顶点内部类型b并不是映射,因此最后还要遍历所有的顶点的b并将其真值拷贝到增量方程的b内
这部分的代码如下:
template
bool BlockSolver::buildSystem()
{
// clear b vector
# ifdef G2O_OPENMP
# pragma omp parallel for default (shared) if (_optimizer->indexMapping().size() > 1000)
# endif
for (int i = 0; i < static_cast(_optimizer->indexMapping().size()); ++i) {
OptimizableGraph::Vertex* v=_optimizer->indexMapping()[i];
assert(v);
v->clearQuadraticForm();
}
_Hpp->clear();
if (_doSchur) {
_Hll->clear();
_Hpl->clear();
}
// resetting the terms for the pairwise constraints
// built up the current system by storing the Hessian blocks in the edges and vertices
# ifndef G2O_OPENMP
// no threading, we do not need to copy the workspace
JacobianWorkspace& jacobianWorkspace = _optimizer->jacobianWorkspace();
# else
// if running with threads need to produce copies of the workspace for each thread
JacobianWorkspace jacobianWorkspace = _optimizer->jacobianWorkspace();
# pragma omp parallel for default (shared) firstprivate(jacobianWorkspace) if (_optimizer->activeEdges().size() > 100)
# endif
for (int k = 0; k < static_cast(_optimizer->activeEdges().size()); ++k) {
OptimizableGraph::Edge* e = _optimizer->activeEdges()[k];
e->linearizeOplus(jacobianWorkspace); // jacobian of the nodes' oplus (manifold)
e->constructQuadraticForm();
# ifndef NDEBUG
for (size_t i = 0; i < e->vertices().size(); ++i) {
const OptimizableGraph::Vertex* v = static_cast(e->vertex(i));
if (! v->fixed()) {
bool hasANan = arrayHasNaN(jacobianWorkspace.workspaceForVertex(i), e->dimension() * v->dimension());
if (hasANan) {
std::cerr << "buildSystem(): NaN within Jacobian for edge " << e << " for vertex " << i << std::endl;
break;
}
}
}
# endif
}
// flush the current system in a sparse block matrix
# ifdef G2O_OPENMP
# pragma omp parallel for default (shared) if (_optimizer->indexMapping().size() > 1000)
# endif
for (int i = 0; i < static_cast(_optimizer->indexMapping().size()); ++i) {
OptimizableGraph::Vertex* v=_optimizer->indexMapping()[i];
int iBase = v->colInHessian();
if (v->marginalized())
iBase+=_sizePoses;
v->copyB(_b+iBase);
}
return 0;
}
上述完成整个矩阵块的构建之后,接下来就是激动人心的求解线性方程的时候了,主要依靠块求解器BlockSolver的solve函数,下面是过程:
(1) 判断是否要做schur消元,如果不做的话,则认为整个图中没有要margin的点,因此直接求解HppΔx=−b 就可以了;
(2) 如果要进行schur消元,则在后面构建出schur需要的矩阵和向量,由于这部分内容比较大,这里就不做展开,感兴趣的可以看SLAM中的marginalization 和 Schur complement,里面讲的也比较清楚
该部分源码如下:
template
bool BlockSolver::solve(){
//cerr << __PRETTY_FUNCTION__ << endl;
if (! _doSchur){
number_t t=get_monotonic_time();
bool ok = _linearSolver->solve(*_Hpp, _x, _b);
G2OBatchStatistics* globalStats = G2OBatchStatistics::globalStats();
if (globalStats) {
globalStats->timeLinearSolver = get_monotonic_time() - t;
globalStats->hessianDimension = globalStats->hessianPoseDimension = _Hpp->cols();
}
return ok;
}
// schur thing
// backup the coefficient matrix
number_t t=get_monotonic_time();
// _Hschur = _Hpp, but keeping the pattern of _Hschur
_Hschur->clear();
_Hpp->add(*_Hschur);
//_DInvSchur->clear();
memset(_coefficients.get(), 0, _sizePoses*sizeof(number_t));
# ifdef G2O_OPENMP
# pragma omp parallel for default (shared) schedule(dynamic, 10)
# endif
for (int landmarkIndex = 0; landmarkIndex < static_cast(_Hll->blockCols().size()); ++landmarkIndex) {
const typename SparseBlockMatrix::IntBlockMap& marginalizeColumn = _Hll->blockCols()[landmarkIndex];
assert(marginalizeColumn.size() == 1 && "more than one block in _Hll column");
// calculate inverse block for the landmark
const LandmarkMatrixType * D = marginalizeColumn.begin()->second;
assert (D && D->rows()==D->cols() && "Error in landmark matrix");
LandmarkMatrixType& Dinv = _DInvSchur->diagonal()[landmarkIndex];
Dinv = D->inverse();
LandmarkVectorType db(D->rows());
for (int j=0; jrows(); ++j) {
db[j]=_b[_Hll->rowBaseOfBlock(landmarkIndex) + _sizePoses + j];
}
db=Dinv*db;
assert((size_t)landmarkIndex < _HplCCS->blockCols().size() && "Index out of bounds");
const typename SparseBlockMatrixCCS::SparseColumn& landmarkColumn = _HplCCS->blockCols()[landmarkIndex];
for (typename SparseBlockMatrixCCS::SparseColumn::const_iterator it_outer = landmarkColumn.begin();
it_outer != landmarkColumn.end(); ++it_outer) {
int i1 = it_outer->row;
const PoseLandmarkMatrixType* Bi = it_outer->block;
assert(Bi);
PoseLandmarkMatrixType BDinv = (*Bi)*(Dinv);
assert(_HplCCS->rowBaseOfBlock(i1) < _sizePoses && "Index out of bounds");
typename PoseVectorType::MapType Bb(&_coefficients[_HplCCS->rowBaseOfBlock(i1)], Bi->rows());
# ifdef G2O_OPENMP
ScopedOpenMPMutex mutexLock(&_coefficientsMutex[i1]);
# endif
Bb.noalias() += (*Bi)*db;
assert(i1 >= 0 && i1 < static_cast(_HschurTransposedCCS->blockCols().size()) && "Index out of bounds");
typename SparseBlockMatrixCCS::SparseColumn::iterator targetColumnIt = _HschurTransposedCCS->blockCols()[i1].begin();
typename SparseBlockMatrixCCS::RowBlock aux(i1, 0);
typename SparseBlockMatrixCCS::SparseColumn::const_iterator it_inner = lower_bound(landmarkColumn.begin(), landmarkColumn.end(), aux);
for (; it_inner != landmarkColumn.end(); ++it_inner) {
int i2 = it_inner->row;
const PoseLandmarkMatrixType* Bj = it_inner->block;
assert(Bj);
while (targetColumnIt->row < i2 /*&& targetColumnIt != _HschurTransposedCCS->blockCols()[i1].end()*/)
++targetColumnIt;
assert(targetColumnIt != _HschurTransposedCCS->blockCols()[i1].end() && targetColumnIt->row == i2 && "invalid iterator, something wrong with the matrix structure");
PoseMatrixType* Hi1i2 = targetColumnIt->block;//_Hschur->block(i1,i2);
assert(Hi1i2);
(*Hi1i2).noalias() -= BDinv*Bj->transpose();
}
}
}
//cerr << "Solve [marginalize] = " << get_monotonic_time()-t << endl;
// _bschur = _b for calling solver, and not touching _b
memcpy(_bschur.get(), _b, _sizePoses * sizeof(number_t));
for (int i=0; i<_sizePoses; ++i){
_bschur[i]-=_coefficients[i];
}
G2OBatchStatistics* globalStats = G2OBatchStatistics::globalStats();
if (globalStats){
globalStats->timeSchurComplement = get_monotonic_time() - t;
}
t=get_monotonic_time();
bool solvedPoses = _linearSolver->solve(*_Hschur, _x, _bschur.get());
if (globalStats) {
globalStats->timeLinearSolver = get_monotonic_time() - t;
globalStats->hessianPoseDimension = _Hpp->cols();
globalStats->hessianLandmarkDimension = _Hll->cols();
globalStats->hessianDimension = globalStats->hessianPoseDimension + globalStats->hessianLandmarkDimension;
}
//cerr << "Solve [decompose and solve] = " << get_monotonic_time()-t << endl;
if (! solvedPoses)
return false;
// _x contains the solution for the poses, now applying it to the landmarks to get the new part of the
// solution;
number_t* xp = _x;
number_t* cp = _coefficients.get();
number_t* xl=_x+_sizePoses;
number_t* cl=_coefficients.get() + _sizePoses;
number_t* bl=_b+_sizePoses;
// cp = -xp
for (int i=0; i<_sizePoses; ++i)
cp[i]=-xp[i];
// cl = bl
memcpy(cl,bl,_sizeLandmarks*sizeof(number_t));
// cl = bl - Bt * xp
//Bt->multiply(cl, cp);
_HplCCS->rightMultiply(cl, cp);
// xl = Dinv * cl
memset(xl,0, _sizeLandmarks*sizeof(number_t));
_DInvSchur->multiply(xl,cl);
//_DInvSchur->rightMultiply(xl,cl);
//cerr << "Solve [landmark delta] = " << get_monotonic_time()-t << endl;
return true;
}
最后就是把得到的Δx对应的调用顶点中的oplusImpl函数对状态变量进行更新
总结
以上就是整个g2o在私底下为我们做的事情了,当然其中很多细节这里没有展现出来,本来看这部分源码的意图也是为了验证过程是否和自己想象的一样,最后的感觉是从数学上来讲大致上是相同的,但是要是从程序上觉得还是受益匪浅,作者的很多编程方式和方法还是很值得学习的。
四. 信息矩阵
H=JTWJ,b=JWe,J是误差对位姿等的雅克比,W是权重。一般这个H矩阵也称为信息矩阵,并且H矩阵是稀疏的.
信息矩阵 和信息向量,其实是另一组描述高斯分布的参数,叫做canonical parameterization.在GraphSLAM中,我们需要通过优化信息矩阵来求得合理的pose和map
总结:
信息矩阵等于协方差的逆,在图优化中作为不确定性的度量。这个矩阵主要是在构成最小二乘优化问题的时候用到的,其实理解成权重更好,协方差越大,说明距离真值的误差越大,那么在优化的时候就要给予较小的权重,不至于误差较大的顶点或者边带偏了整个优化。
参考资料
白巧克力唯心 graph slam tutorial : 从推导到应用1-3
高翔:深入理解图优化与g2o:g2o篇
graph slam学习:g2o
关于g2o的学习使用
泡泡机器人公开课第三十一课:G2O简介 by 姚二亮
g2o系列教程-强烈推荐
api 函数帮助