基于Python的股票数据分析工具的设计与实现——聚类DBSCAN

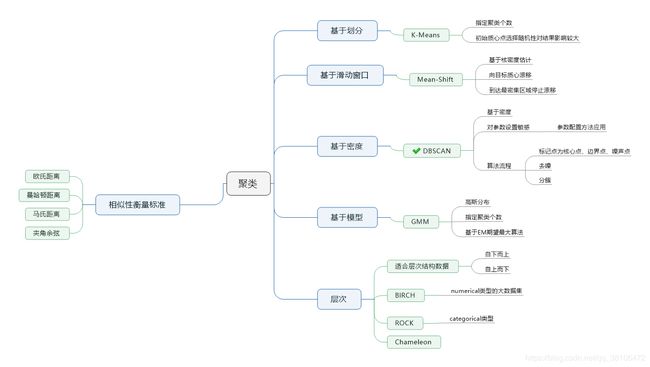
一、聚类（无监督学习）
相信每一个投资者都明白“不要把鸡蛋放在同一个篮子”的投资道理。股市看似“各自为政”，但实际上，看似完全无关的股票是相关的。那么为了规避风险，将相关性极强的股票加以归类则十分重要。
选择对多支股票数据聚类分析，意义：经过对股票交易数据聚类（把整体形态比较相似的聚为一类）后，可以将其分为几个类别，然后从每个类别中选一个样本，最后组成的样本可使样本之间的相关系数降至最低。 这样保证在一定的风险下使收益更高。
按照投资组合优化理论选取标准为：
（1）资产数越多越好
（2）资产之间相关系数越低越好

以期望收益E来衡量证券收益，以收益的方差δ^2表示投资风险
　　minδ2(rp)=∑∑wiwjcov(ri,rj)minδ2(rp)=∑∑wiwjcov(ri,rj)
　　E(rp)=∑wiriE(rp)=∑wiri
　　式中：
　　rp——组合收益；
　　riri——第i种、第j种资产的收益；
　　wiwi——资产i和资产j在组合中的权重；
　　δ2(rp)——组合收益的方差即组合的总体风险；
　　cov(r,rj)——两种资产之间的协方差。

二、思路

• 研究聚类方法，寻找适合处理自己数据的聚类方法，最终敲定DBSCAN
• 基于DBSCAN对于参数设定的敏感性，参考知网论文《DBSCAN 聚类算法的参数配置方法研究》
• 对聚类结果分析并应用于自己的数据

三、数据预处理

• 对多只股票对应的csv文件进行合并 merging.csv

from numpy import nan as NA
import numpy as np
import pandas as pd
import glob


csv_list = glob.glob('*.csv')
for i in csv_list:
    fr = open(i,'rb').read()
    with open('result.csv','ab') as f:
        f.write(fr)

注意合并后的result.csv文件含有多个表头行，可以利用excel的筛选功能对多余的表头行进行删除

• 合并后产生result.csv文件，依次运行data_clustering_parameter.py（确定两个重要阈值Eps、Minpts）和data_cluser.py（查看聚类结果）
• 聚类因子——以name为groupby单位，每支股票的收盘价和成交量方差

四、聚类分析（对某支股票其中两列——开盘价、成交量进行聚类分析）

• 对DBSCAN参数探索的源码data_clustering_parameter.py（参考知网论文《DBSCAN 聚类算法的参数配置方法研究》）

import numpy as np
import numpy.linalg as la
import pandas as pd
import seaborn as sns
#import matplotlib.pyplot as plt
import datetime
#分块读入文件避免Memory Error
#f = open('result.csv',mode = 'r+',encoding = 'UTF-8')
#data = pd.read_csv(f,sep=',',engine = 'python',iterator=True,parse_dates = True)
#loop = True
#chunksize = 1000
#chunks = []
#index=0
#while loop:
#    try:
#        print(index)
#        chunk = data.get_chunk(chunksize)
#        chunks.append(chunk)
##        print(chunks)
#        index+=1
#
#    except StopIteration:
#        loop = False
#        print("Iteration is stopped.")
#print('开始合并')
#data0 = pd.concat(chunks)
#data0 = pd.DataFrame(data0,columns = ['日期','股票代码','名称','收盘价','最高价','最低价','开盘价','前收盘','涨跌额','涨跌幅','换手率','成交量','成交金额','总市值','流通市值'])
#print(data0)   #日期是float64类型
f = open('result.csv',encoding = 'UTF-8')
data0 = pd.read_csv(f,header = 0)
start = datetime.datetime.now()
data = np.array(data0[['name','close','volume']])
print(data)

#求收盘价一列以及成交量一列的协方差
df = pd.DataFrame(data,columns=["name", "close", "volume"])
#df.set_index(["名称"], inplace=True)
df = df.convert_objects(convert_numeric=True)
print(df)
#grouped = df['close'].groupby(df['name'])
grouped1 = df.groupby('name').close.var()
grouped2 = df.groupby('name').volume.var()
print(grouped1)
print(grouped2)
#print(grouped.dtype)

#元组为元素的列表
#data = [(data[i][0],data[i][1]) for i in range(0,len(data))]
data = pd.DataFrame([grouped1,grouped2]).T
data = np.array(data)



#data0 = data0.convert_objects(convert_numeric=True)   #把dataframe各列由object转换为各自对应的数据类型
#print(data0.dtypes)
#data = np.array(data0[['收盘价','成交量']])
#计算距离矩阵
def compute_squared_ED_method(X):
    m,n = X.shape
    #初始化距离矩阵
    D = np.zeros([m, m])
    for i in range(m): 
        for j in range(i, m):
            D[i,j] = la.norm(X[i] - X[j])
            D[j,i] = D[i,j]
    return D
data = compute_squared_ED_method(data)

#对行向量进行排序
data.sort(1)
#对列向量进行排序
data.sort(0)
colValue = ['r', 'y', 'g', 'b', 'c', 'k', 'm']

#绘制每一列距离值的概率密度分布曲线图
for k in range(len(data)):
    sns.kdeplot(pd.Series(data[:,k]),color=colValue[k%len(colValue)])
#绘制第k列数据升序之后的曲线图
#for k in range(len(data)):
#    plt.plot(list(range(len(data))),data[:,k],color=colValue[k%len(colValue)])
#plt.show()
    
end = datetime.datetime.now()
print('Running Time:%s Seconds',end-start)

运行结果如下：
a.绘制第k列数据升序之后的曲线（用于确定Minpts，大致为6）

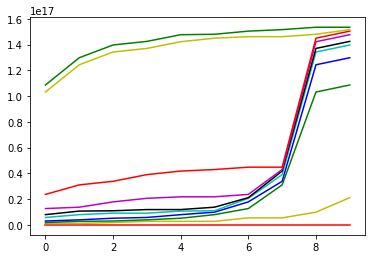
b.概率密度分布曲线图（用于确定Eps，大致为1.6e17）

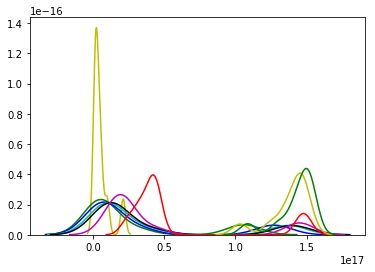
• 聚类源码data_cluster.py（参考周志华的《机器学习》）

import math
import numpy as np
import pandas as pd
#import matplotlib.pyplot as plt
#import matplotlib as mpl
#from pylab import *
#mpl.rcParams['font.sans-serif'] = ['SimHei']
import pylab as pl
import datetime
f = open('result.csv',encoding = 'UTF-8')
data0 = pd.read_csv(f,header = 0)

start = datetime.datetime.now()

data = np.array(data0[['name','close','volume']])
print(data)

#求收盘价一列以及成交量一列的协方差
df = pd.DataFrame(data,columns=["name", "close", "volume"])
#df.set_index(["名称"], inplace=True)
df = df.convert_objects(convert_numeric=True)   #把dataframe各列由object转换为各自对应的数据类型
print(df)
#grouped = df['close'].groupby(df['name'])
grouped1 = df.groupby('name').close.var()
grouped2 = df.groupby('name').volume.var()
#print(grouped1)
#print(grouped2)
#print(grouped.dtype)

#元组为元素的列表
#data = [(data[i][0],data[i][1]) for i in range(0,len(data))]
data = pd.DataFrame([grouped1,grouped2]).T
data = np.array(data)
data = [(float(data[i][0]),float(data[i][1])) for i in range(0,len(data))]
#print(data.loc[0,:])
#print(data.loc['ABC',:])

#计算欧几里得距离,a,b分别为两个元组
def dist(a, b):
    return math.sqrt(math.pow(a[0]-b[0], 2)+math.pow(a[1]-b[1], 2))  #计算二维欧氏距离

#算法模型
def DBSCAN(D, Eps, Minpts):   #数据集D,邻域半径Eps,密度阈值Minpts
    #初始化核心对象集合T,聚类个数k,聚类集合C, 未访问集合P,找出所有核心点
    T = set(); k = 0; C = []; P = set(D)
    for d in D:
        if len([ i for i in D if dist(d, i) <= Eps]) >= Minpts:
            T.add(d)
    #开始聚类，生成聚类簇
    while len(T):
        #记录当前未访问样本集合
        P_old = P
        #随机选取一个核心对象，并于未访问集合删除
        o = list(T)[np.random.randint(0, len(T))]
        P = P - set(o)
        #初始化队列Q
        Q = []; Q.append(o)
        while len(Q):
            #取出队列中首个样本
            q = Q[0]
            Nq = [i for i in D if dist(q, i) <= Eps]
            if len(Nq) >= Minpts:
                S = P & set(Nq)
                Q += (list(S))
                P = P - S
            Q.remove(q)
        #Q每为空一次，便生成一个新的聚类簇
        k += 1
        Ck = list(P_old - P)
        T = T - set(Ck)
        C.append(Ck)
    return C

#画图
def draw(C):
    colValue = ['y', 'r', 'g', 'b', 'c', 'k', 'm']
    for i in range(len(C)):
        coo_X = []    #x坐标列表
        coo_Y = []    #y坐标列表
        for j in range(len(C[i])):
            #定位到元组中的第0和1项
            coo_X.append(C[i][j][0])
            coo_Y.append(C[i][j][1])
        pl.scatter(coo_X, coo_Y, marker='o', color=colValue[i%len(colValue)], label=i)

    pl.legend(loc='upper right')
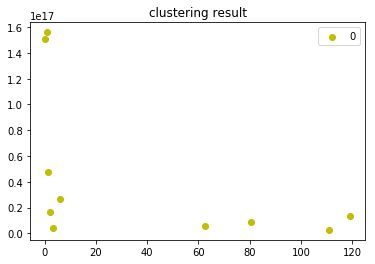
    pl.title('clustering result')
    pl.show()




C = DBSCAN(data,1.6e17, 6)
draw(C)
end = datetime.datetime.now()
print('Running Time:%s Seconds',end-start)

运行结果如下：

五、预测
预测源码prediction.py

#Importing Libraries  
import numpy as np
import pandas as pd
import talib

#Setting the random seed to a fixed number
import random
random.seed(42)

#Importing the dataset
dataset = pd.read_csv('RELIANCE.NS.csv')
dataset = dataset.dropna()
dataset = dataset[['Open', 'High', 'Low', 'Close']]

#数据准备
dataset['H-L'] = dataset['High'] - dataset['Low']
dataset['O-C'] = dataset['Close'] - dataset['Open']
#3天移动平均线
dataset['3day MA'] = dataset['Close'].shift(1).rolling(window = 3).mean()
#10天移动平均线
dataset['10day MA'] = dataset['Close'].shift(1).rolling(window = 10).mean()
#30天移动平均线
dataset['30day MA'] = dataset['Close'].shift(1).rolling(window = 30).mean()
#5天内平均方差
dataset['Std_dev']= dataset['Close'].rolling(5).std()
#相对强弱指数
dataset['RSI'] = talib.RSI(dataset['Close'].values, timeperiod = 9)
#威廉指数
dataset['Williams %R'] = talib.WILLR(dataset['High'].values, dataset['Low'].values, dataset['Close'].values, 7)
#输出值为股价涨幅
dataset['Price_Rise'] = np.where(dataset['Close'].shift(-1) > dataset['Close'], 1, 0)
#处理缺失值
dataset = dataset.dropna()

X = dataset.iloc[:, 4:-1]
y = dataset.iloc[:, -1]

#拆分数据集，80%为训练集
split = int(len(dataset)*0.8)
X_train, X_test, y_train, y_test = X[:split], X[split:], y[:split], y[split:]

#特征缩放
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)

#Building the Artificial Neural Network
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import Dropout

#变量分类器
classifier = Sequential()

#搭建两个隐藏层
classifier.add(Dense(
        units = 128, 
        kernel_initializer = 'uniform', 
        activation = 'relu', 
        input_dim = X.shape[1]
        ))
classifier.add(Dense(
        units = 128, 
        kernel_initializer = 'uniform', 
        activation = 'relu'
        ))
#一个输出层
classifier.add(Dense(
        units = 1, 
        kernel_initializer = 'uniform', 
        activation = 'sigmoid'
        ))
classifier.compile(
                   optimizer = 'adam', 
                   loss = 'mean_squared_error', 
                   metrics = ['accuracy']
                   )

#编译分类器
classifier.fit(X_train, y_train, batch_size = 10, epochs = 100)


#预测股票动向
y_pred = classifier.predict(X_test)
y_pred = (y_pred > 0.5)

dataset['y_pred'] = np.NaN
dataset.iloc[(len(dataset) - len(y_pred)):,-1:] = y_pred
trade_dataset = dataset.dropna()

#Computing Strategy Returns
trade_dataset['Tomorrows Returns'] = 0.
trade_dataset['Tomorrows Returns'] = np.log(trade_dataset['Close']/trade_dataset['Close'].shift(1))
trade_dataset['Tomorrows Returns'] = trade_dataset['Tomorrows Returns'].shift(-1)

trade_dataset['Strategy Returns'] = 0.
trade_dataset['Strategy Returns'] = np.where(
                    trade_dataset['y_pred'] == True, 
                    trade_dataset['Tomorrows Returns'], 
                    - trade_dataset['Tomorrows Returns']
                    )

trade_dataset['Cumulative Market Returns'] = np.cumsum(trade_dataset['Tomorrows Returns'])
trade_dataset['Cumulative Strategy Returns'] = np.cumsum(trade_dataset['Strategy Returns'])

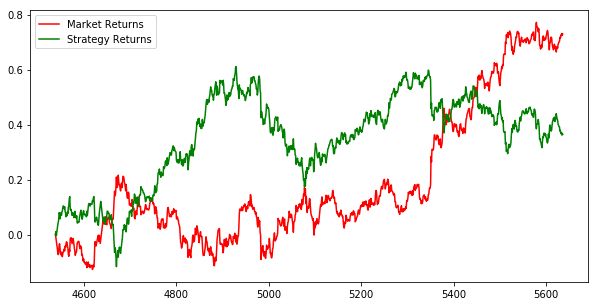
#市场收益和模型收益的走势图
import matplotlib.pyplot as plt
plt.figure(figsize=(10,5))
plt.plot(trade_dataset['Cumulative Market Returns'], color='r', label='Market Returns')
plt.plot(trade_dataset['Cumulative Strategy Returns'], color='g', label='Strategy Returns')
plt.legend()
plt.show()

预测结果