LeetCode股票类问题集体秒
文章目录
- 解题框架
- 121. 买卖股票的最佳时机
- 122. 买卖股票的最佳时机 II
- 309. 最佳买卖股票时机含冷冻期
- 714. 买卖股票的最佳时机含手续费
- 123. 买卖股票的最佳时机 III
- 188. 买卖股票的最佳时机 IV
解题框架
每一个状态的含义,比如:
dp[3][2][1] 的含义就是:今天是第三天,我现在手上持有着股票,至今最多进行 2 次交易。
dp[2][3][0] 的含义:今天是第二天,我现在手上没有持有股票,至今最多进行 3 次交易。
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
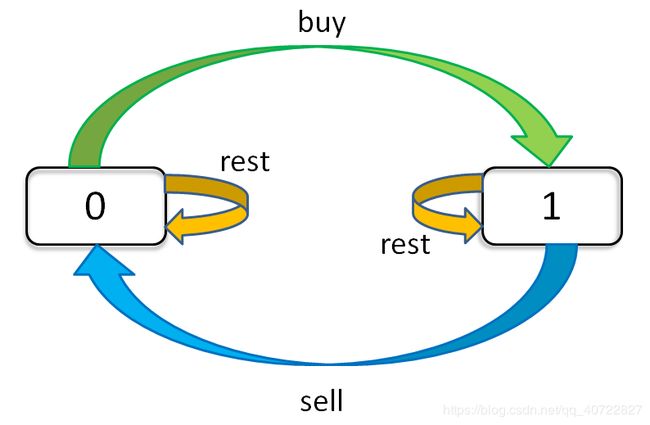
max( 选择 rest , 选择 sell )
解释:今天我没有持有股票,有两种可能:
要么是我昨天就没有持有,然后今天选择 rest,所以我今天还是没有持有;
要么是我昨天持有股票,但是今天我 sell 了,所以我今天没有持有股票了。
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])
max( 选择 rest , 选择 buy )
解释:今天我持有着股票,有两种可能:
要么我昨天就持有着股票,然后今天选择 rest,所以我今天还持有着股票;
要么我昨天本没有持有,但今天我选择 buy,所以今天我就持有股票了。
dp[-1][k][0] = 0
解释:因为 i 是从 0 开始的,所以 i = -1 意味着还没有开始,这时候的利润当然是 0 。
dp[-1][k][1] = -infinity
解释:还没开始的时候,是不可能持有股票的,用负无穷表示这种不可能。
dp[i][0][0] = 0
解释:因为 k 是从 1 开始的,所以 k = 0 意味着根本不允许交易,这时候利润当然是 0 。
dp[i][0][1] = -infinity
解释:不允许交易的情况下,是不可能持有股票的,用负无穷表示这种不可能。
- 框架总结
base case:
dp[-1][k][0] = dp[i][0][0] = 0
dp[-1][k][1] = dp[i][0][1] = -infinity
状态转移方程:
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])
121. 买卖股票的最佳时机
-
原题地址
-
正常套模板
class Solution {
public int maxProfit(int[] prices) {
int len = prices.length;
if(len==0){
return 0;
}
int[][] dp = new int[len][2];
for(int i = 0;i<len;i++){
if(i-1 == -1 || i-2 == -2){
dp[i][0] = 0;
dp[i][1] = -prices[i];
continue;
}
dp[i][0] = Math.max(dp[i-1][0],dp[i-1][1]+prices[i]);
dp[i][1] = Math.max(dp[i-1][1],-prices[i]);
}
return dp[len-1][0];
}
}
- 注意一下状态转移方程,新状态只和相邻的一个状态有关,其实不用整个 dp 数组,只需要一个变量储存相邻的那个状态就足够了,这样可以把空间复杂度降到 O(1)。(
这个技巧可以在所有的状态方程里用。)
class Solution {
public int maxProfit(int[] prices) {
int len = prices.length;
if(len==0){
return 0;
}
int dp_i_0 = 0, dp_i_1 = Integer.MIN_VALUE;
for(int i = 0;i<len;i++){
if(i-1 == -1){
dp_i_0 = 0;
dp_i_1 = -prices[i];
continue;
}
dp_i_0 = Math.max(dp_i_0,dp_i_1+prices[i]);
dp_i_1 = Math.max(dp_i_1,-prices[i]);
}
return dp_i_0;
}
}
122. 买卖股票的最佳时机 II
-
原题地址
-
如果 k 为正无穷,那么就可以认为 k 和 k - 1 是一样的。可以这样改写框架:
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])
= max(dp[i-1][k][1], dp[i-1][k][0] - prices[i])
我们发现数组中的 k 已经不会改变了,也就是说不需要记录 k 这个状态了:
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i])
- 代码实现
class Solution {
public int maxProfit(int[] prices) {
int len = prices.length;
if(len==0){
return 0;
}
int dp_i_0 = 0;
int dp_i_1 = Integer.MIN_VALUE;
for(int i = 0;i<len;i++){
dp_i_0 = Math.max(dp_i_0,dp_i_1+prices[i]);
dp_i_1 = Math.max(dp_i_1,dp_i_0-prices[i]);
}
return dp_i_0;
}
}
309. 最佳买卖股票时机含冷冻期
- 原题地址
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1], dp[i-2][0] - prices[i])
解释:第 i 天选择 buy 的时候,要从 i-2 的状态转移,而不是 i-1 。
- 正常套模板
class Solution {
public int maxProfit(int[] prices) {
int len = prices.length;
if(len==0){
return 0;
}
int[][] dp = new int[len][2];
int dp_i_2 = 0;
for(int i = 0;i<len;i++){
if(i-1==-1){
dp[i][0] = 0;
dp[i][1] = -prices[i];
continue;
}
int temp = dp[i-1][0];
dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i]);
dp[i][1] = Math.max(dp[i-1][1], dp_i_2 - prices[i]);
dp_i_2 = temp;
}
return dp[len-1][0];
}
}
- 改进
class Solution {
public int maxProfit(int[] prices) {
int n = prices.length;
int dp_i_0 = 0, dp_i_1 = Integer.MIN_VALUE;
int dp_pre_0 = 0; // 代表 dp[i-2][0]
for (int i = 0; i < n; i++) {
int temp = dp_i_0;
dp_i_0 = Math.max(dp_i_0, dp_i_1 + prices[i]);
dp_i_1 = Math.max(dp_i_1, dp_pre_0 - prices[i]);
dp_pre_0 = dp_i_0;
}
return dp_i_0;
}
}
714. 买卖股票的最佳时机含手续费
- 原题地址
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i] - fee)
解释:相当于买入股票的价格升高了。
在第一个式子里减也是一样的,相当于卖出股票的价格减小了。
- 在
122. 买卖股票的最佳时机 II这题的基础上,在每次买入的时候扣掉手续费。即dp_i_0-prices[i]-fee。
class Solution {
public int maxProfit(int[] prices, int fee) {
int len = prices.length;
if(len==0){
return 0;
}
int dp_i_0 = 0;
int dp_i_1 = Integer.MIN_VALUE;
for(int i = 0;i<len;i++){
dp_i_0 = Math.max(dp_i_0,dp_i_1+prices[i]);
dp_i_1 = Math.max(dp_i_1,dp_i_0-prices[i]-fee);
}
return dp_i_0;
}
}
123. 买卖股票的最佳时机 III
- 原题地址
class Solution {
public int maxProfit(int[] prices) {
int len = prices.length;
if(len==0) return 0;
int max_k = 2;
int[][][] dp = new int[len][max_k+1][2];
for(int i=0;i<len;i++){
for (int k = max_k; k >= 1; k--){
if (i - 1 == -1){
dp[i][k][0] = 0;
dp[i][k][1] = -prices[i];
continue;
}
dp[i][k][0] = Math.max(dp[i-1][k][0], dp[i-1][k][1] + prices[i]);
dp[i][k][1] = Math.max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i]);
}
}
return dp[len - 1][max_k][0];
}
}
- 这里 k 取值范围比较小,所以可以不用 for 循环,直接把 k = 1 和 2 的情况全部列举出来也可以。
dp[i][2][0] = max(dp[i-1][2][0], dp[i-1][2][1] + prices[i])
dp[i][2][1] = max(dp[i-1][2][1], dp[i-1][1][0] - prices[i])
dp[i][1][0] = max(dp[i-1][1][0], dp[i-1][1][1] + prices[i])
dp[i][1][1] = max(dp[i-1][1][1], -prices[i])
class Solution {
public int maxProfit(int[] prices) {
int dp_i10 = 0, dp_i11 = Integer.MIN_VALUE;
int dp_i20 = 0, dp_i21 = Integer.MIN_VALUE;
for (int price : prices) {
dp_i20 = Math.max(dp_i20, dp_i21 + price);
dp_i21 = Math.max(dp_i21, dp_i10 - price);
dp_i10 = Math.max(dp_i10, dp_i11 + price);
dp_i11 = Math.max(dp_i11, -price);
}
return dp_i20;
}
}
188. 买卖股票的最佳时机 IV
- 原题地址
/**
当k大于等于数组长度一半时, 问题退化为贪心问题此时采用 买卖股票的最佳时机 II
的贪心方法解决可以大幅提升时间性能, 对于其他的k, 可以采用 买卖股票的最佳时机 III
的方法来解决, 在III中定义了两次买入和卖出时最大收益的变量, 在这里就是k租这样的
变量, 即问题IV是对问题III的推广, t[i][0]和t[i][1]分别表示第i比交易买入和卖出时
各自的最大收益
**/
class Solution {
public int maxProfit(int max_k, int[] prices) {
int n = prices.length;
if(n==0) return 0;
if (max_k > n / 2)
return maxProfit(prices);
int[][][] dp = new int[n][max_k+1][2];
for(int i=0;i<n;i++){
for (int k = max_k; k >= 1; k--){
if (i - 1 == -1){
dp[i][k][0] = 0;
dp[i][k][1] = -prices[i];
continue;
}
dp[i][k][0] = Math.max(dp[i-1][k][0], dp[i-1][k][1] + prices[i]);
dp[i][k][1] = Math.max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i]);
}
}
return dp[n - 1][max_k][0];
}
private int maxProfit(int[] prices) {
int len = prices.length;
int dp_i_0 = 0;
int dp_i_1 = Integer.MIN_VALUE;
for(int i = 0;i<len;i++){
dp_i_0 = Math.max(dp_i_0,dp_i_1+prices[i]);
dp_i_1 = Math.max(dp_i_1,dp_i_0-prices[i]);
}
return dp_i_0;
}
}
你知道的越多,你不知道的越多。
有道无术,术尚可求,有术无道,止于术。
如有其它问题,欢迎大家留言,我们一起讨论,一起学习,一起进步