牧场物语 FZU (必须多线DP，不可以两次DP，也就是不可以来回各DP一次)

题目大意很简单理解就不贴题了

很多人dp两次，就是WA，我在网上也没有找到为啥不能这样，全都是双线dp，估计很多写双线dp的都不懂为什么不能两次dp，

我的思路就是：从起点dp到终点，回溯过去，把路过的点全都标记为0，继续从起点dp到终点（和从终点回到起点是一样的），两次dp的和作为answer，

果然和大家一样是WA

按我个人理解分析一下：

先给出一组数据：

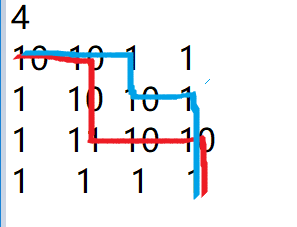
用两次dp的答案就是 74

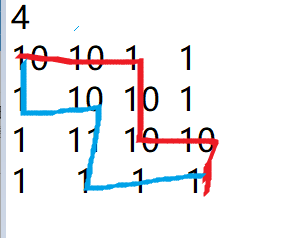
而正确答案是  76

 

显而易见，两次dp的路线分别为蓝线和红线，这是最优解吗，NO！

这个才是最优解！！！很明显图二有4个1没走，肯定大于图一有6个1没走

小结一下：两次dp，可以分别得到最优解，没错，但是合起来不一定是最优解。

就好比贪心算法，局部最优不一定是全局最优。

两次dp代码如下，WA

#include 

using namespace std;
typedef long long ll;
ll z[105][105];
ll dp[105][105];
int f(int a,int b)
{
    if(a==0 || b==0) return dp[a][b]=0;
    if(dp[a][b]!=-1) return dp[a][b];
    return dp[a][b] = max(f(a-1,b),f(a,b-1)) + z[a][b];
}
void back(int a,int b)//回溯把走过的路径找出来
{
    if(a==0 || b==0) return ;
//    printf("%d %d\n",dp[a][b],z[a][b]);
    if(dp[a-1][b] == dp[a][b]-z[a][b])
    {
        z[a][b]=0;
        back(a-1,b);
    }
    else
    {
        z[a][b]=0;
        back(a,b-1);
    }
}
int main()
{
    int n;
    while(cin>>n)
    {
        for(int i=1; i<=n; i++)
            for(int j=1; j<=n; j++)
                cin>>z[i][j];
        memset(dp,-1,sizeof dp);
        ll sum=f(n,n);
        back(n,n);
        memset(dp,-1,sizeof dp);
        ll ans=sum+f(n,n);
        cout<

双线dp代码如下，AC

思路简单说一下：以考虑为有两个人一起出发，从起点到终点，路上取得最大权值。
dp[k,(x1,y1),(x2,y2)]=max{
                    dp[k-1,(x1,y1-1),(x2,y2-1)]+a[x1,y1]+a[x2,y2]，
                    dp[k-1,(x1,y1-1),(x2-1,y2)]+a[x1,y1]+a[x2,y2]，
                    dp[k-1,(x1-1,y1),(x2,y2-1)]+a[x1,y1]+a[x2,y2]，
                    dp[k-1,(x1-1,y1),(x2-1,y2)]+a[x1,y1]+a[x2,y2]  }
容易得到上述方程，k代表第几步，其他的都是字面意思。
然后x和y和k之间有关系，k+1=x+y，显然可以减掉两维了。状态化简为dp[k][x1][x2]。因为k状态只由k-1的状态转移而来。

难点是坐标怎么表示，网上很多神犇都有解答我就不累赘了。

#include 

using namespace std;
typedef long long ll;
int z[105][105];
ll dp[250][105][105];
int main()
{
    int n;
    while(cin>>n)
    {
        for(int i=1;i<=n;i++)
            for(int j=1;j<=n;j++)
                cin>>z[i][j];
        memset(dp,-0x3f3f3f3f,sizeof dp);
        dp[1][1][1]=z[1][1];
        for(int step=2;step<=2*n-1;step++)//共步数
        {
            for(int i=1;i<=n;i++)
                for(int j=1;j<=n;j++)
                {
                    dp[step][i][j] = max(max(dp[step-1][i-1][j],dp[step-1][i][j-1]),max(dp[step-1][i][j],dp[step-1][i-1][j-1]));
                    if(j!=i)
                        dp[step][i][j] += z[i][step+1-i] + z[j][step+1-j];
                    else
                        dp[step][i][j] +=z[i][step+1-i];//此时这i,j重合
                }
        }
        cout<

希望大家可以指出错误，蒟蒻OvO......

有关多线dp的简单介绍可以看一下这个https://blog.csdn.net/qq_40733911/article/details/81292072