2019牛客暑期多校训练（第一场）E-ABBA（卡特兰数的扩展）（超级无敌巨详细）

前言

距离第一场已过去一周多，这一题在我脑海中挥之不去，当时没做出来，知道要贪心，仅仅暴力出了小规模的结果，队友发现m=0和n=0时结果是卡特兰数，如今在恶补了一些卡特兰数的习题后，我终于对这题有了较为清晰的认识。下面结合卡特兰数的一种应用——非降路径，以组合数学的角度分析一下这题。

题目

题目链接

E.ABBA

题目大意

给定m，n，共(m+n)个’A’，(m+n)个’B’，组成长度为2*(m+n)的字符串，字符串要能拆分出n个"AB"和m个"BA"，求能组成该类字符串的方案数。

题意理解

哪里用到了贪心

样例给了n=1,m=2，方案数是13，用暴力程序跑的结果：

解释一下这里用的贪心，拿ABABAB举例

可以按图左拆分也可以按图右拆分，这里按图右方式拆分，即：先出现的’A’用来组成"AB"，组成n个"AB"后还剩下的’A’用来组成"BA"；先出现的’B’用来组成"BA"，组成m个"BA"后还剩下的’B’用来组成"AB"。

哪里出现了卡特兰数

令m=0(或者n=0，这不重要，一个等于0就行了）

1，1，2，5，14，42， 132， 429，1430，4862…
没错，这就是大名鼎鼎的卡特兰数。
令f(2n)表示m为0时的方案数，那么原问题就是长为2n的序列要能拆分出n对"AB"，原先接触过卡特兰数的应该很熟悉，这里的A可以对应于出栈顺序问题中的入栈，B则是出栈；A可以对应于括号匹配问题中的左括号，B则是右括号；A可以对应于非降路径y=x下方（可位于y=x）的右移，B则是上移等等

也就是说，在序列的前i位中，‘A’的数量要>=‘B’的数量，1<=i<=2*n。
第一位一定要是’A’，与之匹配的’B’一定要是偶数位，不然中间是奇数个’A’、‘B’，显然无法满足上述条件。（我习惯以1开始计数）
可以得出，f(2n)=f(0)*f(2n-2)+f(2)*f(2n-4)+…+f(2n-2)*f(0)。
f(0)*f(2n-2)的意思是：第2位为’B’且与第1位的’A’相匹配，剩余字符分为两个部分，一部分为0个字符，另一部分为2n-2个字符；
f(2)*f(2n-4)的意思是：第4位为’B’且与第1位的’A’相匹配，剩余字符分为两个部分，一部分为2个字符，另一部分为2n-4个字符；
…
显然，f(2n)=h(n)（h(n）表示卡特兰数的第n项，h(0)=1，h(1)=1，h(2)=2）。

同样的也很显然，m!=0时情况又变复杂了。下面数形结合，理解一下卡特兰数的扩展：

非降路径

预备知识0

• 在一个水平网格上，从(0,0)开始向右或向上每次走一步，共走n+m步可到达点(n,m)，每一条路径称为一条非降路径。
• 上述非降路径与卡特兰数相关的联系
• 组合数公式（高中知识即可）
• (0,0)到(n,m)的非降路径条数是C(n+m,n)
• (s,t)到(n,m)的非降路径条数C(n-s+m-t,n-s)

预备知识1

• 从(0,0)到(n,n)且不穿过对角线y=x（除了(0,0)和(n,n)，可以走到x==y的点）（可以走下方，也可以走上方，方案数是一样的，这里是走下方）的问题等价于上面的ABBA问题（当m=0时，要有n对"AB"）(上面也提到过）

• 从(0,0)到(n,m)且不穿过对角线y=x（可以走到x==y的点，下方）有个隐含条件是不经过直线y=x+1（这一点记住）

证明(0,0)到(n,m)且不经过y=x的非降路径条数

注意这里是不经过、n>=m

1. 不考虑不合法的情况，为C(n+m,n)种
2. (0,0)先向上走到(0,1)，那么到终点(n,m)一定会经过y==x，这种非法的情况为(0,1)到(n,m)的非将路径条数C(n+m-1,n)
3. (0,0)先向右走到(1,0)，这时有两种情况，情况a为合法的，情况b是还会经过y==x的，这时候记该路线第一次经过y=x的点为C，将(1,0)到点C间的路径关于y=x对称，可得到与情况2的一一映射，即情况b的不合法路径数同样为C(n+m-1,n)
4. 总的满足条件的路径条数为C(n+m,n)-2*C(n+m-1,n)，也可以只考虑走下边的情况，即C(n+m-1,m)-C(n+m-1,n)
   

证明(0,0)到(n,m)且不穿过y=x的非降路径条数

注意这里是不穿过（(0,0)除外）、n>=m
不穿过y=x，回忆一下，也就是条件是任意时刻向上的步数不能小于等于向右的步数。
我们来从反面考虑，不穿过y=x的补集也就是经过y=x+1。下面来求从(0,0)到(n,m)经过y=x+1的路径条数（其实在上面一条已经证过了），设这样的一条路径与y=x+1第一个交点为B，将(0,0)到B点的路径关于y=x+1对称，即得到(-1,1)到B点再到(n,m)的非降路径。相反，也能从(-1,1)对称回来，所以是个一一映射。而(-1,1)到(n,m)的非降路径条数为C(n+m,n+1)。
故(0,0)到(n,m)且不穿过y=x的非降路径条数为C(m+n,n)-C(n+m,n+1)。

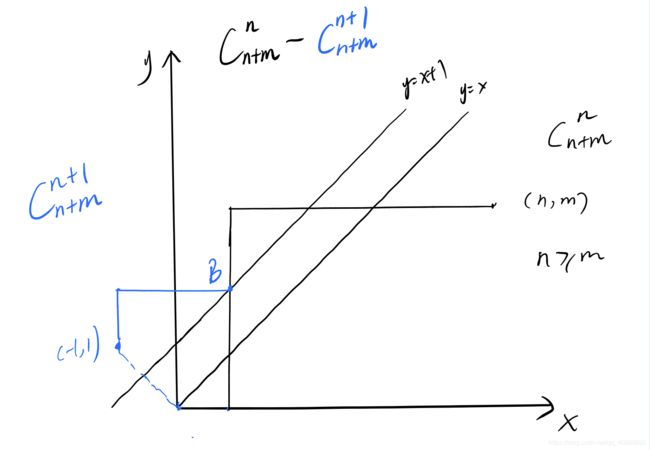
也可以把(n,m)点变换到(n+1,m)点，就变成上个问题了。

证明(0,0)到(n,m)且不经过y=x+k的非降路径条数

注意这里是不经过、n>=m、k>=0
原理同上，合法的=总的-非法的

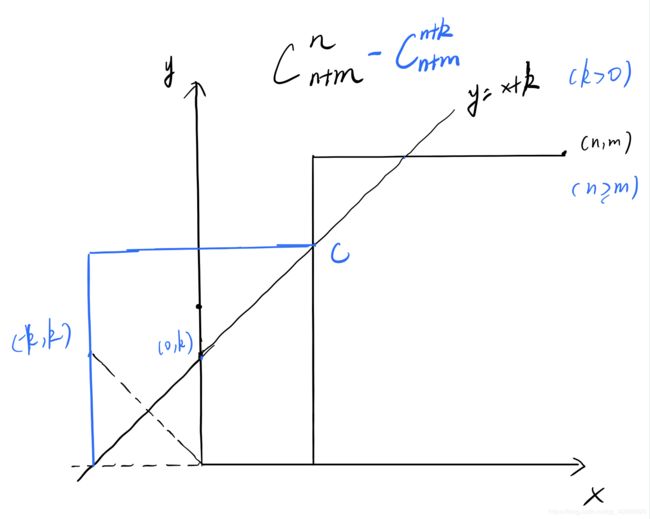
(0,0)到(n,m)且不经过y=x+k的非降路径条数为C(m+n,n)-C(m+n,n+k)

问题转换

说了那么多废话 ，开始解决这道题吧！
根据前面贪心讲的，假设现在用了x个字符’A’，y个字符’B’，那么可以得到：
x-n<=y（'A’先用来组成n个"AB"，剩下x-n个’A’要小于等于’B’的个数，不然匹配不了足够的"BA"）；
y-m<=x（'B’先用来组成m个"BA"，剩下y-m个’B’要小于等于’A’的个数，不然匹配不了足够的"AB"）。
利用上面的非降路径，小于等于对应“穿过”，为了换成“经过”，经历如下变换：（m>=0,n>=0）
不穿过y=x+m变成，不经过y=x+m+1；
不穿过y=x-n变成，不经过y=x-n-1;

可以套公式。也就是求(0,0)关于y=x+m+1的对称点（-m-1,m+1），和(0,0)关于y=x-n-1的对称点(n+1,-n-1)。然后：

结束语

这题还有很多人用DP，这里就不考虑了。
这题用组合数学真的很巧妙，可能是我见识少吧。
我再一次被数学的神奇给震撼到了，可惜我是个数学渣。
知识浅薄，若有错误之处请告知。
这里附上我做过的卡特兰数的习题：https://www.cnblogs.com/wangzhebufangqi/p/11250198.html

参考资料

[1]蒙双惠.非降路径与栈的计数[J].河北大学学报(自然科学版),1995(03):25-28.
[2]李占兰.格子图中具有一定限制条件的非降路径数[J].青海师范大学学报（自然科学版）,2007,(3):6-7. DOI:10.3969/j.issn.1001-7542.2007.03.002.
[3]2019牛客暑期多校训练营（第一场）E.ABBA(带限制条件的非降路径)
[4]2019牛客暑期多校训练营（第一场）E.ABBA
[5]网上众多的相关博客

代码

一开始的暴力代码

//检查小规模数据用
#include
using namespace std;
const int MAXN=1e3+5;
const int MAXM=1e3+5;
const int MOD=1e9+7;
int m,n;
char a[(MAXM+MAXN)<<1];
vector<int> indexA,indexB;
bool isok()
{
	for(int i=1,j=m+1;i<=n;++i,++j)
	if(indexA[i]>indexB[j]) return false;
	for(int i=n+1,j=1;j<=m;++i,++j)
	if(indexA[i]<indexB[j]) return false;
	return true;
}
int main()
{
	/*ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);*/
	while(~scanf("%d%d",&n,&m))
	{
		int len=m+n;
		for(int i=1;i<=len;++i)
		a[i]='A',a[len+i]='B';
		int ans=0;
		do
		{
			indexA.clear();indexB.clear();
			indexA.push_back(0);indexB.push_back(0);
			for(int i=1;i<=len+len;++i)
			if(a[i]=='A') indexA.push_back(i);
			else indexB.push_back(i);
			if(isok())
			{
				//cout<<(a+1)<
				ans++;
			}	
		}while(next_permutation(a+1,a+len*2+1));
		cout<<ans<<endl;
	}
}

AC代码（Java）

import java.util.Scanner;
import java.math.BigInteger;
import java.io.BufferedInputStream;
public class Main {
    static final int MAXN=1000+5;
    static final int MAXM=1000+5;
    static final int MOD=1000000000+7;
    static BigInteger fac[]=new BigInteger[(MAXN+MAXM)<<1+5];
    static int n,m;
    public static void Init()
    {
        fac[0]=BigInteger.ONE;
        int len=(MAXN+MAXM)<<1;
        for(int i=1;i<=len;++i) fac[i]=fac[i-1].multiply(BigInteger.valueOf(i));
        return;
    }
    public static void main(String[] args) {
        Scanner cin=new Scanner(new BufferedInputStream(System.in));
        Init();
        while(cin.hasNext())
        {
            n=cin.nextInt();m=cin.nextInt();
            BigInteger total=fac[2*(m+n)].divide(fac[m+n].multiply(fac[m+n]));
            BigInteger sub1=n==0?BigInteger.ZERO:fac[2*(m+n)].divide(fac[2*m+n+1].multiply(fac[n-1]));
            BigInteger sub2=m==0?BigInteger.ZERO:fac[2*(m+n)].divide(fac[2*n+m+1].multiply(fac[m-1]));
            total=total.subtract(sub1);
            total=total.subtract(sub2);
            total=total.mod(BigInteger.valueOf(MOD));
            System.out.println(total);
        }
        cin.close();
    }
 
}