洛谷春季 ACM 多校训练 第五场(A-H)(无EH)
难度
简单:C、F、G
中等:A、D
难题:B、E、H
目录
- A题 T127117 Ammunition
- 题目类型 :数学
- 题目链接 :
- 题目大意 :
- 解题思路 :
- 代码 :
- B题 T127119 Bolshevik
- 题目类型 :
- 题目链接 :
- 题目大意 :
- 解题思路 :
- 代码 :
- C题 T127120 Change
- 题目类型 :二分图匹配问题
- 题目链接 :
- 题目大意 :
- 解题思路 :
- 解法,匈牙利算法 ([Hungary讲解](https://blog.csdn.net/dark_scope/article/details/8880547))
- 代码 :
- 解法一,匈牙利算法
- D题 T127122 Duliu
- 题目类型 :数学,数据结构,算法
- 题目链接 :
- 题目大意 :
- 解题思路 :
- 代码 :
- E题 T127123 Earthquake
- 题目类型 :
- 题目链接 :
- 题目大意 :
- 解题思路 :
- 代码 :
- F题 T127124 Flaw
- 题目类型 :简单数学
- 题目链接 :
- 题目大意 :
- 解题思路 :
- 代码 :
- G题 T127125 Gene
- 题目类型 :DP
- 题目链接 :
- 题目大意 :
- 解题思路 :
- 代码 :
- H题 T127126 Heartfelt Fancy
- 题目类型 :
- 题目链接 :
- 题目大意 :
- 解题思路 :
- 代码 :
- 总结
A题 T127117 Ammunition
题目类型 :数学
题目链接 :
T127117 Ammunition
题目大意 :
现在有三个物品,第一种值是a,第二种值是b,第三种值在[0,b/2]中任选,物品的值是整数,现在拿了n个物品,问值的和是否可能是m,保证a 注意了第三种的值是可以选择0的。 已知 b>a 所以 如果 m > b*n 是必然不可能的 注意:读入的数据比较大,需要使用scanf或者关流 T127119 Bolshevik T127120 Change 给你n个题,每个题都有 k i k_i ki个单词,每个题选择一个单词的首字母去进行匹配,可以调换题的顺序(意思就是你第一题的首字母可以和第二第三甚至是最后的其中一个字母去进行匹配),问是否’a’到’a+n-1’都能有匹配,有则输出Yes不能就输出‘No’。 来自于出题人的题解 二分图匹配问题,所以想到匹配中的匈牙利大法。 就通过样例2来看,我们可以把每一种选择化成集合,就比如第一组集合,你可以选择a或者a –在实现代码的时候,我更喜欢用数字去代替char类型的数据 那么匈牙利算法中的匹配就是1匹配1、n匹配n,直接套板子就可以 T127122 Duliu 前缀和 由题目可以知道是对 sigma( maxpre(x,i) ) * sigma( maxsuf(i+1,x) )求和,该式子就是答案的贡献 最大的前缀和,比如这里是[1,y]在最后push_back( x )的时候 有关平衡树的题,例题CF题但是是需要打标记,本题不用打标记 解法二、 总时间复杂度O(n) 解法二 T127123 Earthquake T127124 Flaw 在计算机中我们通常把两个数相加超出整数所能表示的范围成为整数溢出。 不等式可能为 a + n 1 < n 2 a+n1 < n2 a+n1<n2 也可能为 a + n 1 > n 2 a+n1 > n2 a+n1>n2 就是可能是大于也可能是小于,那么就会存在两种溢出方式 –据说枚举端点不回超时也可得出答案 T127125 Gene 给定两个DNA,其中匹配成功是alpha分,匹配失败是-beta分,gap是-gamma分,问最大匹配 什么是gap呢?就是你可以在任意位置添加任意数量的gap,如果匹配的是gap的话,就是扣除-gamma分 输入n,m表示字符串的长度,成功匹配得到α,失败匹配减去β,没匹配到扣γ分 首先题目中出现了gap匹配的问题,这很好解决,两个gap匹配不可能最优,这里的两个gap是指母串i位置加一个gap子串i位置也加一个gap,有点整体后移的感觉,所以两个字符串相对来说没有变化,反而增加了gap匹配,所以题解中也提到了两个gap匹配一定不会最优 整个子串匹配母串的最优解,求解整体的最优解就需要用到动态规划(dp)了,每步最优求解最局最优 d p [ i ] [ j ] dp[i][j] dp[i][j] 表示母串的前i个位置和子串的前j个位置匹配的最大收益 第一部分是只考虑一个gap匹配,后面考虑的是匹配成功还是失败 时间复杂度O(nm) T127126 Heartfelt Fancy 关于BEH如果有时间,再加上水平进步会对这三题进行补全解题思路 :
接下来需要考虑的就是覆盖区间的问题,这就取决与你取值问题了,我们可以把a的值看做是一类,剩余的数字是一类,先假设为全部都是b,那么下一步就是进行替换,将x个b值替换为[0, b/2]再将y个值替换为0,进而进行分析
注意:数据范围大!用__int128解决代码 :
int main(){
int t; RD(t);
while(t--){
LL n, m, a, b; bool flag = false; scanf( "%lld%lld%lld%lld" , &n , &m , &a , &b );
if (n == 0){
if (m == 0){OT("Yes"); continue; } else { OT("No"); continue;}
}
if ( ( ( __int128)(n - 1)) * b + (b / 2) >= m) flag = true; //区间[0, (n-1) * b + (b / 2)]
else if ( ( ( ( __int128) n) * b - m ) < 0) flag = false; // n * b < m
else if ( ( ( ( __int128) n ) * b - m ) % ( b - a ) == 0 ) {
if( ( ( ( __int128 ) n ) * b - m ) / ( b - a ) <= n ) flag = true;
else flag = false;
}
else flag = false;
flag ? OT("Yes") : OT("No");
}
}
B题 T127119 Bolshevik
题目类型 :
题目链接 :
题目大意 :
解题思路 :
代码 :
C题 T127120 Change
题目类型 :二分图匹配问题
题目链接 :
题目大意 :
解题思路 :
把每个题的每个名字转换为这个题能否用第i个字母开头
然后每个题到每个可以开头的字母连一条边
转换为一个二分图匹配问题,相当于问是否存在满的匹配
使用dinic算法:O(n^2.5)
使用矩阵乘法:O(n^2.373)
不知道是否有准确一点的界,对这种图论了解不多解法,匈牙利算法 (Hungary讲解)

接下来是匹配,发现h字母没有与之匹配的对象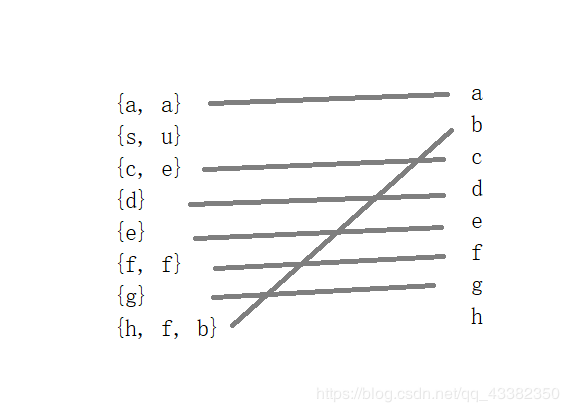
那我们再换种匹配方法,h是有人匹配了,但b又没人去和他匹配了

所以显然样例2的输出是Noint temp = s[0] - 'a' + 1;
代码 :
解法一,匈牙利算法
//rep和for都是循环
#define ECH(it, A) for (__typeof((A).begin()) it=(A).begin(); it != (A).end(); ++it)
const int N = 1e5 + 50;
VC adj[N]; bool vy[N]; int py[N];
//vc = vectorD题 T127122 Duliu
题目类型 :数学,数据结构,算法
题目链接 :
题目大意 :
解题思路 :
考虑正向扫一遍反向扫一遍分别算出每个位置i的sigma( maxpre(x,i) )与sigma( maxsuf(i+1,x) )
如果[y,end()]的和>0,我们把这一段加入最大前缀
用个数据结构维护所有位置的maxpre与这个位置到i的和,这个的差,如果这个差<0,则我们的maxpre需要更新为这个位置到i的和,否则不用更新
改数据结构支持:
1.全局加x
2.全局和
3.全局<0的变成0
4.插入一个元素
考虑我们可以每次先插入一个0,然后全局加x,然后全局<0的变成0
所以可以用一个栈来维护代码 :
int n , a[ MAXN ];
long long maxpre[ MAXN ] , maxsuf[ MAXN ] , ans;
int main()
{
cin >> n;
for( int i = 1 ; i <= n ; i++ ) cin >> a[i];
for( int l = 1 ; l <= n ; l++ )
for( int r = l + 1 ; r <= n ; r++ )
{
maxpre[l - 1] = 0;
long long now = 0;
for( int i = l ; i <= r - 1 ; i++ )
{
now += a[i];
maxpre[i] = max( maxpre[i - 1] , now );
}
maxsuf[r + 1] = 0;
now = 0;
for( int i = r ; i >= l + 1 ; i-- )
{
now += a[i];
maxsuf[i] = max( maxsuf[i + 1] , now );
}
for( int i = l ; i <= r - 1 ; i++ )
ans = ( ans + ( maxpre[i] % mod ) * ( maxsuf[i + 1] % mod ) ) % mod;
}
cout << ans << endl;
return 0;
}
E题 T127123 Earthquake
题目类型 :
题目链接 :
题目大意 :
解题思路 :
代码 :
F题 T127124 Flaw
题目类型 :简单数学
题目链接 :
题目大意 :
现在题目给你一个不等式,要你考虑有多少个解决整数溢出的方案?解题思路 :
我这里就称为向上溢出和向下溢出,n1、n2的范围题目中已经给了 [−2147483648, 2147483647].大于的时候要解决上溢就是a的范围在[n2, 2147483647]这样任意一个值相加都不会出现溢出的情况(我这样理解应该没问题,有问题请指出)所以解决的方案数就有2147483647 - n2
;小于的时候同理。代码 :
int main(){
//cout << 2147483647 - 2147484162 << '\n';
LL n1, n2; char a, b, c;
scanf("%c%c%lld%c%lld", &b, &a, &n1, &c, &n2);
if (c == '>'){
cout << 2147483647 - n2 << '\n';
}
else{
cout << 2147483648 + n2 << '\n';
}
}
G题 T127125 Gene
题目类型 :DP
题目链接 :
题目大意 :
解题思路 :
dp[i][j] = max( max(dp[i - 1][j], dp[i][j - 1]) - gamma, dp[i - 1][j - 1]+(a[i] == b[j] ? alpha : -beta));
代码 :
const int maxn = 5050;
LL dp[maxn][maxn];
void init(LL n, LL m,LL gamma){
for(int i=0;i<=n;i++) dp[i][0]= -i * gamma;
for(int i=0;i<=m;i++) dp[0][i]= -i * gamma;
}
int main(){
LL n, m, alpha, beta, gamma;
cin >> n >> m >> alpha >> beta >> gamma;
string a, b; cin >> a >> b;
a = " " + a; b = " " + b;
init(n, m, gamma);
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++){
dp[i][j] = max( max(dp[i - 1][j], dp[i][j - 1]) - gamma, dp[i - 1][j - 1]+(a[i] == b[j] ? alpha : -beta));
}
}
OT(dp[n][m]);
}
H题 T127126 Heartfelt Fancy
题目类型 :
题目链接 :
题目大意 :
解题思路 :
代码 :
总结
