量子计算入门基础学习笔记(二 量子算符与张量)
艰难困苦 玉汝于成
- 一 . 矩阵与量子算符
- (1)外积
- (2) 投影算符
- (3)逆算符
- (4)厄米算符 Hermitian operators
- (5)幺正 算符 Unitary
- 二 . 张量与量子比特
- (1)概念理解
- (2)张量运算与量子比特对
欢迎来到量子计算专栏的第二节,抱着打破不要自学量子力学魔咒的勇气,我们接着第一节内容的学习,回顾一下,我们之前介绍了狄拉克符号,量子比特,希尔伯特空间,还有算符的一些基础知识,在此基础上,这节内容将会为大家介绍几种重要的算符 ,还有张量的一丢丢东西!
一 . 矩阵与量子算符
紧接着上篇博客,了解了算符的本质,性质和作用之后,下面深入学习几种重要的算符!
(1)外积
在这之前,我们先看一个东西叫 外积,我相信大家乍一看这个词“外积”,是既熟悉又陌生啊,我隐约记得高数下册里面学空间几何的时候好像用它来求过一个空间平面的法向量,那到了线代和量子力学中,外积又是啥呢?
内积我们现在都知道长成这样: ⟨ α ∣ β ⟩ \left \langle\alpha | \beta \right \rangle ⟨α∣β⟩ ,我的通俗理解就是的两边狄拉克符中的箭头都朝外,相反,所以叫内积,故而,我大胆猜测,外积就是这里两个箭头朝内,嘻嘻 ,事实的结果也不出我们所料:
算符 ∣ α ⟩ ⟨ β ∣ \left| \alpha \right \rangle \left \langle \beta \right | ∣α⟩⟨β∣ 被定义为外积 :
( ∣ α ⟩ ⟨ β ∣ ) ∣ γ ⟩ = ∣ α ⟩ ( ⟨ β ∣ γ ⟩ ) = ( ⟨ β ∣ γ ⟩ ) ∣ α ⟩ (\left| \alpha \right \rangle \left \langle \beta \right |) \left| \gamma \right \rangle = \left| \alpha \right \rangle(\left \langle\beta | \gamma \right \rangle) = (\left \langle\beta | \gamma \right \rangle) \left| \alpha \right \rangle (∣α⟩⟨β∣)∣γ⟩=∣α⟩(⟨β∣γ⟩)=(⟨β∣γ⟩)∣α⟩
这是相对于内积而言的,这里需要特别注意: 外积的本质是一个算符,是一个矩阵,不是和内积一样为某个数!,我觉得大家这个时候拿出草稿纸随便写几个态矢量算一算比较好!。
(2) 投影算符
我们假设 ∣ a ⟩ \left| a \right \rangle ∣a⟩ 是一个单位矢量,用一个未知的算符 P a P_{a} Pa作用于任意一个矢量 ∣ γ ⟩ \left | \gamma \right \rangle ∣γ⟩ 得到的新矢量 ∣ β ⟩ \left | \beta \right \rangle ∣β⟩为:
∣ β ⟩ = P a ∣ γ ⟩ = ∣ a ⟩ ⟨ a ∣ γ ⟩ = ⟨ a ∣ γ ⟩ ∣ a ⟩ \left| \beta \right \rangle=P_{a} \left| \gamma \right \rangle = \left| a\right \rangle \left \langle a | \gamma \right \rangle = \left \langle a | \gamma \right \rangle \left| a\right \rangle ∣β⟩=Pa∣γ⟩=∣a⟩⟨a∣γ⟩=⟨a∣γ⟩∣a⟩
那么,这里的 P a P_{a} Pa我们就叫它 投影算符 直接看这个式子理解可能会有点懵,仔细想想不难看出 ⟨ a ∣ γ ⟩ \left \langle a | \gamma \right \rangle ⟨a∣γ⟩ 是内积,本质是一个数,最后的结果就是一个数乘上单位矢量 ∣ a ⟩ \left| a \right \rangle ∣a⟩ ,总结来说就是:将一个一般矢量 ∣ γ ⟩ \left| \gamma \right \rangle ∣γ⟩ 投影到单位矢量 ∣ a ⟩ \left| a\right \rangle ∣a⟩上,得到新矢量的方向与 ∣ a ⟩ \left| a\right \rangle ∣a⟩方向相同,长度为 ∣ a ⟩ \left| a\right \rangle ∣a⟩和 ∣ γ ⟩ \left| \gamma\right \rangle ∣γ⟩的内积
它有一些如下的性质:

这里的子空间我们日后再叙,量子的学习过程中,我们难免会遇到许多新的高级名词,我认为这就像做英语阅读题一样,不会的单词先跳过去,随着我们水平的提升,都会逐渐解决的!
(3)逆算符
先介绍定义:
A B = B A = I AB=BA=I AB=BA=I
那么,算符 B B B称为 A A A的逆,记为 B = A − 1 B=A^{-1} B=A−1 ,在矢量表达式中,若 ∣ β ⟩ = A ∣ α ⟩ \left |\beta \right \rangle= A \left | \alpha \right \rangle ∣β⟩=A∣α⟩ ,则有 ∣ α ⟩ = A − 1 ∣ β ⟩ \left | \alpha \right \rangle=A^{-1}\left |\beta \right \rangle ∣α⟩=A−1∣β⟩,这里和我在线代中的逆矩阵有异曲同工之妙!
(4)厄米算符 Hermitian operators
对于希尔伯特空间 H 中的任意线性算符 A,都有存在且唯一的线性算符 A + A^{+} A+,(注意,这里的符号和伴随矩阵不一样,切勿混淆!),称为 A 的伴随或厄米共轭算符,其与空间H中的所有矢量 ∣ α ⟩ \left| \alpha \right \rangle ∣α⟩, ∣ β ⟩ \left| \beta \right \rangle ∣β⟩都满足以下关系:
⟨ α ∣ A β ⟩ = ⟨ A + α ∣ β ⟩ \left \langle \alpha |A\beta \right \rangle = \left \langle A^{+}\alpha |\beta \right \rangle ⟨α∣Aβ⟩=⟨A+α∣β⟩
大家注意,这里由于csdn不支持这么高级的公式输入。。。。。
我将这个厄米算符的上标改成了 + 号,其实他是长下图这样的, 大家知道就好了 :
![]()
即一个算符A先作用于 ∣ β ⟩ \left| \beta \right \rangle ∣β⟩得到的新矢量再与 ∣ α ⟩ \left| \alpha \right \rangle ∣α⟩作内积,其结果与 A 的厄米算符 A + A^{+} A+直接作用于 ∣ α ⟩ \left| \alpha \right \rangle ∣α⟩的结果再和 ∣ β ⟩ \left| \beta \right \rangle ∣β⟩作内积的结果是一样的!这个算符干嘛用的 ,有啥性质呢?
我们都知道算符的本质是一个矩阵,而厄米算符想表达的就是厄米矩阵! 那厄米矩阵是什么呢?

重要性:量子力学中的力学量用算符来表示,而实验上的可观测的物理量要用厄米算符来表示。因此,要弄清物理量的特点,研究厄米算符的性质就显得尤为重要!
这就又和波函数扯上关系了,我醉了~~
性质:
![]()
我们到后面的深入研究时会经常用到这个算符,大家一定要掌握这个东西!

(5)幺正 算符 Unitary
这个和厄米算符与逆算符是捆绑销售的!
如果算符 U 存在如下关系:
U U + = U + U = I UU^{+} = U^{+}U= I UU+=U+U=I
那么, U就被定义为幺正算符!显然:幺正算符的厄米共轭就是它的逆算符,即 U + = U − 1 U^{+} = U^{-1} U+=U−1。
同样,其本质就是幺正矩阵(酉矩阵)!
若酉矩阵的元素都是实数,其即为正交矩阵(实矩阵)。与正交矩阵G不会改变两个实向量的内积类似: ( G x , G y ) = ( x , y ) \left ( G_{x},G_{y} \right ) = \left ( x,y \right ) (Gx,Gy)=(x,y)
此外,酉矩阵U不改变两个复向量的内积: ( U x , U y ) = ( x , y ) \left ( U_{x},U_{y} \right ) = \left ( x,y \right ) (Ux,Uy)=(x,y)
酉矩阵的特征值都是模为1的复数,即分布在复平面的单位圆上,因此酉矩阵行列式的值也为1!
二 . 张量与量子比特
相信大家在线代的学习过程中都或多或少听到过张量这个名词,虽然在大一的线代课中并没有关于它的内容,但这绝不影响它在量子计算领域独一无二的位置!下面,我们结合量子比特来了解一下!
(1)概念理解
什么是张量呢?它只是我们对矩阵认识在多维空间的升级版而已!

看了这个图,我也就不用再多说什么了,非常形象的告诉了我们各阶张量的是啥东西!可是这个三维张量我们能想到,那四维,五维的呢?
先把三维张量画成一个立方体:
接着就简单了,和前面的思路一样:

这样,就可以无限延伸了,和数据结构里面的那个啥 高维数组有点像!
这个方法是为了大家能更好的通俗理解,“张量”在不同的运用场景下有不同的定义,我们先理解到这,后面再深入!
(2)张量运算与量子比特对
通过上面,我们可以认为张量也可以像向量和矩阵一样有运算法则,我们以向量为例给出一个m维向量与n维向量的张量乘积 体会一下:
[ a 1 a 2 ⋮ a m ] ⨂ [ b 1 b 2 ⋮ b n ] = [ a 1 b 1 ⋮ a 1 b n a 2 b 1 ⋮ a 2 b n ⋮ a m b n ] \begin{bmatrix} a_{1} \\ a_{2} \\ \vdots \\ a_{m} \end{bmatrix} \bigotimes \begin{bmatrix} b_{1} \\ b_{2} \\ \vdots \\ b_{n} \end{bmatrix} =\begin{bmatrix} a_{1}b_{1}\\ \vdots \\ a_{1}b_{n} \\ a_{2}b_{1} \\ \vdots \\ a_{2}b_{n} \\ \vdots \\ a_{m} b_{n} \end{bmatrix} ⎣⎢⎢⎢⎡a1a2⋮am⎦⎥⎥⎥⎤⨂⎣⎢⎢⎢⎡b1b2⋮bn⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡a1b1⋮a1bna2b1⋮a2bn⋮ambn⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤
矩阵相乘的条件比较苛刻,第一个矩阵的的列数必须和第二个矩阵的行数相等,这个张量就宽泛多了,依次相乘!
回到主题上来,We all know, 量子态可以叠加的物理特性是实现量子并行计算的基础,量子态能够纠缠是实现信息高速且不可破译的理论前提!我们开始定量的从张量角度学习这个。
量子态中的 ∣ 0 ⟩ \left| 0 \right \rangle ∣0⟩ 和 ∣ 1 ⟩ \left| 1 \right \rangle ∣1⟩ ,该对量子比特用矩阵定义为:
∣ 0 ⟩ ≡ ( 1 0 ) ∣ 1 ⟩ ≡ ( 0 1 ) \left| 0 \right \rangle \equiv \begin{pmatrix}1 \\0\end{pmatrix} \qquad \left| 1 \right \rangle \equiv \begin{pmatrix}0 \\1 \end{pmatrix} ∣0⟩≡(10)∣1⟩≡(01)
这一对量子比特有可以组成4个不重复的比特对:
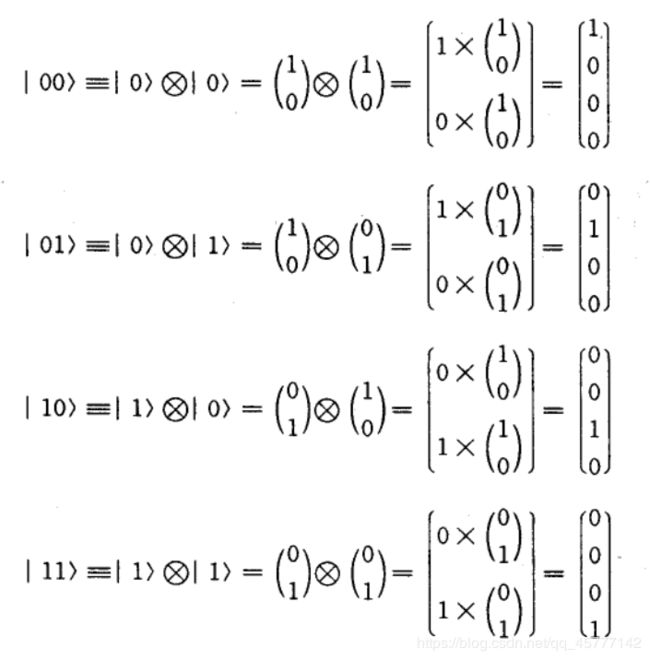
注意,这已经是四维空间的向量了!
好,这一次的量子计算博客学习就到这里了,如果大家发现有错误的地方可以在评论区留言,本人会及时改正,觉得博主写的还可以的可以点点关注,点点赞!本人基本上是每周一更,希望大家支持!