Houdini Vellum 之 Graph Color 的算法分析

Houdini 18 的Vellum目前使用的是更高级的PBD: XPBD(eXtended Position Based Dynamics) 。XPBD使用了2^nd Order Integration ，传统的PBD使用的1^nd  Order Intergration 。想要查看的话，如下图（默认是2^nd Order Integration)。

Vellum Solver中因为要对约束重复的运算（Constraint Iterations 设置迭代的次数），需要比较高的效率。 为了能够让并行运算，引入了Graph Corlor技术。Graph Color说白了， 就是定义一个属性，每个约束的属性和与它相邻的约束的属性值不同。

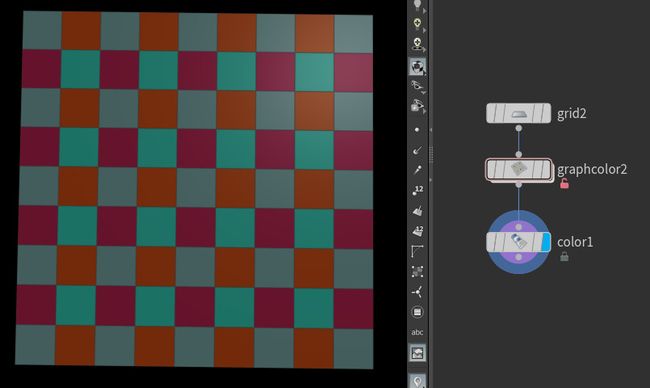
比如用一个Grid，用Vellum Contraints 得到 distant contrainsts ，然后用Graph Color节点进行计算 （结果默认写入在一个整型color属性上），最后用wrangle 显示颜色（相同的color属性颜色相同）， 如下图，能够看到，每一条边（primitive）都与相邻的边的颜色不同。 这样让颜色相同的contrainst在同一个Workset。 不同颜色，不同的Workset。这样在对constrait进行迭代计算时（是在opencl里面进行的），Opencl会根据Workset，同一个Workset才会一起平行计算。

当然，Vellum  中Graph Color的计算时在Vellum Solver内部，这里只是为了演示方便。

另个案例了解Vellum Solver 中 的 Graph Color

新建个一个Grid，选中两边的点， 给Pin Constraints，把两边定住。加 distant constraints ( Vellum Constraint 选 Distant along edges)，设置如下图。注意Stiffness设置为最大(10*1e+10)，这种材质现实中是没有弹性的， 但是我们又把Rest Length Scale设置为0.5，Vellum Solver会迫使它压缩（现实中这种材质的布料是不存在的）。然后把Vellum Solver的 Smooth Iteration 设置为0（这步很重要）。 结算。

 结算后发现，有的边的长度缩短大致0.5倍，有的反而被拉长了。用Graph Color查看，发现拉伸边长的是同一个颜色，即作为同一个WorkSet在opencl中并行计算的。如下图：

 这是因为黄色的边做一个同一个Workset首先在opencl中运算，红色和蓝色在黄色后面分别进行运算，这样导致错误都转嫁到了第一次计算的边上（这里的错误是指，设置了Rest Length Scale为0.5倍，红色和蓝色都正确压缩了，黄色反而拉长了，这是错误的， 不是我们想要的）。

Graph Color 的算法分析

 下面分析下Graph Color节点里面的算法。新建一个Grid，Graph Color， Color（random from attributes）。

进入Graph Color内部， 主要分析最左边这路（Connectivity 为Primtive），Contraints运算的时候也是以Primtive为单位。

（1）create_color_attrib  

         创建 color (Integer)primitive属性

（2）find_npts

          把当前primitive总共有多少邻居记录在属性 @__npts属性上。   

i@__npts = len(primpoints(0, @primnum));

（3）color_high_valence （Run  Over Detail ）

         这步主要是把邻居多的primitive筛选出来（Graph Color 的参数Max Valence设置阈值，默认20），单独计算。因为进入opencl进行并行计算时，需要把邻居primitive写入在一个array数组里，如果相邻的邻居太多，会造成存储和计算时间的极大浪费。挑其中比较重要的代码部分进行分析：

        下面的代码把筛选出来的符合条件的primitve（@__npts>maxvalence） 存入在prims数组里面。　

int maxvalence = chi("maxvalence");
string grp = sprintf("\@__npts>=%d", maxvalence);
int prims[] = expandprimgroup(0, grp);

　　然后对数组进行排序。npts数组记录prims数组中对应的prim的点的数量乘以-1 。argsort对npts数组排序，它返回的是一个indice的数组。

　　indice： 比如一个整型数组  int a[] = {0,4,2} 。a[1] = 4 ，中括号里面的1就是indice, 也就是数组下标。

　　对于一个数组int b[] = {-4，-10，-2，-8} 进行 argsort排序会得到一个数组下标的数组 {1,3,0,2}，最后用reorder函数得到最终的排序数组 {b[1],b[3],b[0],b[2]}  即{ -10，-8，-4，-2}。 （argsort 和reorder一般搭档起来用，来对数组排序）。

foreach(int i; int prim; prims)
{
    npts[i] = -len(primpoints(0, prim));
}
prims = reorder(prims, argsort(npts));

　　最终得到一个数组，根据primitive的点的数量由大到小排列。　　

　　核心的部分在下面这个foreeach部分

foreach(int i; int prim; prims)
{
    int useNewColor = 1;     // 声明新变量，是否使用新颜色，默认1，即使用新染色
    int pts[] = primpoints(0, prim); 
    for(int j = 0; j < ncolors; j++)    // ncolors记录当前不同color的数量， 遍历所有color
    {
        int useColor = 1;       // 声明新变量，能否用当前颜色，默认1， 可以使用
        foreach(int pt; pts)    // 遍历当前primitive的每个点
        {
            if (mapping[j * npt + pt] != 0)   //mapping是一个数组，npts是所有点的数量（不止当前primitive）
            {                                 //比如npts= 14 ，当前primitive2个点，对于j=0,即color值为0 ，mapping[0*14+0]~mappint[0*14+(14-1)] 
                useColor = 0;        //对应的所有的点使用的color 0的情况，mapping值若为1即不等于0， 说明当前color值被邻居占用，不能使用
                break;               // 这是把useColor赋值0， 即当前color值不可用
            }
        }
        if (useColor)                 //如果当前颜色可用
        {
            colors[i] = j;           // 把当前primitive 的color值记录到colors数组里
            foreach(int pt; pts)　　　// 对于当前primitive的所有点pt,color为j,对应mapping[j*npt+pt],设置为1，表示被当前primitive占用

            {
                mapping[j * npt + pt] = 1;  // 
            }
            useNewColor = 0;          // 这种情况就不使用新颜色了
            break;
        }
    }
    if (useNewColor)         //说明没有可用的color,需要新增加一个color
    {
        colors[i] = ncolors;  // 新的color值存到colors数组里，colors[i]是prims[i]对应的颜色值
        ncolors++;            // 总颜色数加1
        resize(mapping, ncolors * npt);   // mapping数组resize,空间比之前多了npt个
        foreach(int pt; pts)
        {
            mapping[colors[i] * npt + pt] = 1;  //对于新增的color[i],当前primitive的点pt, 把对应的mappint[colors[i]*npt+pt]赋值1， 表示被占用
        }
    }
}

 这个节点完整的代码如下：

 1 // Handle high valence prims in a serial pre-pass,
 2 // else the find_neighbors wrangle below ends up creating
 3 // extremely large neighbors arrays, which are expensive
 4 // in memory and time.
 5 int maxvalence = chi("maxvalence");
 6 string grp = sprintf("\@__npts>=%d", maxvalence);
 7 int prims[] = expandprimgroup(0, grp);
 8 int nprim = len(prims);
 9 if (nprim == 0)
10     return;
11 
12 // Create mapping for each point to each color and
13 // prims to each color.
14 int npt = npoints(0);
15 int mapping[];
16 int colors[];
17 resize(colors, nprim);
18 int ncolors = 0;
19 
20 
21 // Reverse sort by num pts in constraint
22 // so constraints with more points are first.
23 int npts[];
24 resize(npts, nprim);
25 foreach(int i; int prim; prims)
26 {
27     npts[i] = -len(primpoints(0, prim));
28 }
29 prims = reorder(prims, argsort(npts));
30 
31 foreach(int i; int prim; prims)
32 {
33     int useNewColor = 1;
34     int pts[] = primpoints(0, prim);
35     for(int j = 0; j < ncolors; j++)
36     {
37         // See if we can use this color.
38         int useColor = 1;
39         foreach(int pt; pts)
40         {
41             if (mapping[j * npt + pt] != 0)
42             {
43                 useColor = 0;
44                 break;
45             }
46         }
47 
48         if (useColor)
49         {
50             colors[i] = j;
51             foreach(int pt; pts)
52             {
53                 mapping[j * npt + pt] = 1;
54             }
55             useNewColor = 0;
56             break;
57         }
58     }
59     if (useNewColor)
60     {
61         colors[i] = ncolors;
62         ncolors++;
63         resize(mapping, ncolors * npt);
64         foreach(int pt; pts)
65         {
66             mapping[colors[i] * npt + pt] = 1;
67         }
68     }
69 }
70 
71 // Set prim color attribute.  Colored prims will be skipped
72 // by the OpenCL pass.
73 foreach(int i; int prim; prims)
74     setprimattrib(geoself(), chs("colorname"), prim, colors[i]);

View Code

 （4）copy_color_to_newcolor

      把color属性复制一份，新属性名：__newcolor。　　这是给opencl用。

（5）find_neighbors

     把所有与当前primitiv相邻的primitive记录在数组@__neighbours数组里。

int neighbors[];
int pts[] = primpoints(0, @primnum);
foreach(int pt; pts)
    foreach(int n; pointprims(0, pt))
        if (n != @primnum)
            append(neighbors, n);
i[]@__neighbors = neighbors;

  (6)  create_offsets_sizes

    设置opencl 的 workset ，@__sizes是所有primitive的数量，@__offsets={0}。即只有一个Workset，这个workset包含所有的primitves。

i[]@__offsets = {0};
i[]@__sizes = array(nprimitives(0));

　　可能会有人产生疑问，就一个workset ？这不和不设置workset一样的吗？所有的primitive都并行执行。这是因为在Opencl中，比如设置了迭代次数（Iteration）为1000，当我们迭代到500时，发现已经达到目的了，所有primitive与和它相邻的primitive 的color值都不同，那么此时可以吧@__sizes设置为0，表明workset的大小为0，不需要继续迭代计算了，这样避免了资源的浪费。

 （7）assign_colors_sizes

      opencl部分，为每个primitive寻找color值。使用的是Gebremedhin-Manne speculative coloring 算法。每一次迭代都分为两部分 （1）寻找color  (2) 解决冲突 ，即当某个primitive与它的相邻primitive是相同的color时，需要重新寻找color

　　（1）寻找color

　　#define MAXFORBID 18446744073709551615ul  这里定义MAXFORBID为64位二进制能表示的最大值，二进制表示为   11111111 -（中间48个1）- 11111111

    if (color[idx] >= 0)    // 说明已经找到color了， 比如前面第三部，为邻居多的primitive提前设置了color,这里就不在重新寻找color了
        return;

    int nidx = neighbors_index[idx];    //nidx是指针，指向与当前primitive的相邻的primitives的第一个primitive
    int nlast = neighbors_index[idx+1]; // nlast也是指针，但实际上它指向与global id 为idx+1的 primitive相邻的第一个primitive
    int c = -1, offset = 0;             // 因为指针是连续存储的，nlast-1 也就指向当前primitive的最后一个primitive
    // Loop until colored.
    while(c < 0)                    // c 小于0说明没找到color ,继续
    {
        // Bit flag to store seen neighbor colors.
        ulong forbidden = 0;　　　// 64位（二进制）forbidden，每一位表示一个color，详见下面注释1
        for(int i = nidx; i < nlast; i++)   //遍历所有邻居primitive
        {
            // Flag any neighbor colors present in the current bitrange.
            int n = neighbors[i];
            int nc = color[n] - offset;   //color[n]是当前邻居的color值
            if (nc >= 0 && nc < FORBIDBITS) // 详见注释2
                forbidden |= (1ul << nc);   //见注释2
        }
        // Check if there's an open color in the current bitrange.
        if (forbidden ^ MAXFORBID)  //forbidden 和 64位全1做二进制与运算
        {
            ulong x = forbidden;     //forbidden值赋值给x
            c = offset;
            // Find position of first zero bit.
            x = (~x) & (x + 1);   // 见注释3， 找最小的color
            // Color is log2(x)
            while(x > 1)     //说明找到颜色
            {
                x /= 2;      //为方便假设x为八位二进制0000 0100 ,表示成10进制数为22 ，这里要循环2次，最终的得到c值为2
                c++;          
            }
        }
        else
        {
            // Otherwise we need to try again with the next range of colors.
            offset += FORBIDBITS;   // 没找到，说明64位不够用，再加64位
        }
    }
    // Record speculative coloring.
    newcolor[idx] = c;

 注释1：

为了表示方便， 我们假设forbidden是八位的二进制。那么forbidden值为0000 0101 表示第0个color(最右边1）和第二个color 已经被占用。

注释2：

color[n]是当前邻居的color值，假设为3 。假设我们64个color值够用，那么此时对应offset = 0。为了方便，假设forbidden值为00000000 00000000 00000000 00000000 00000000 00000000 00000000 00010101。

 nc = color[n] - offset = 3 

1ul << nc ：这是二进制左进位， 1ul 值为  00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000001，1ul<<3， 即相左进三位：

                                                                    00000000 00000000 00000000 00000000 00000000 00000000 00000000 00001000

forbidden |= (1ul << nc)： 二进制或运算

forbidden       : 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00010101

 (1ul << nc)   :  00000000 00000000 00000000 00000000 00000000 00000000 00000000 00001000

或运算结果：   00000000 00000000 00000000 00000000 00000000 00000000 00000000 00011101

把或运算的结果复制给forbidden ，表示第0个，第二个，第三个，第四个 color已经被邻居占用了，不能使用了。forbidden中存在0，表示还有可以使用的color

注释3：

这步利用了二进制运算的一个性质。能很快的找到最小的color。

比如当前 x 值 为                      00000000 00000000 00000000 00000000 00000000 00000000 00000000 00011101

~x 即二进制取反  ：                11111111   11111111   11111111   11111111   11111111   11111111  11111111  11100010

(x + 1)即二进制加1：              00000000 00000000 00000000 00000000 00000000 00000000 00000000 00011110

(~x) & (x + 1) 二进制与运算： 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000010

二进制与运算的结果表示第1个color可以使用（从右往左数，最右边是第0个）

 　　（2）解决冲突

有部分是与（1）相同的，挑重点分析一下。

if (nc == c) // 如果当前primitive与邻居color相同
{
    int nnpt = npts[n];
    if (nnpt > npt || (nnpt == npt && n < idx)) // 设定去改点数少的primitive,或者 idx大的primitive。 
    {
         conflict = 1;     // 那么如果邻居的primitive包含的点数比当前的primitive多，或者点数一样多，但是当前primitive
         break;            // 的idx大， 那设定当前primitive的conflicit为1 ，改当前primitive的color值。
     }
}

 完整的代码如下：

  1 #define FORBIDBITS 64
  2 #define MAXFORBID 18446744073709551615ul
  3 
  4 // Gebremedhin-Manne speculative coloring.
  5 kernel void assigncolors( 
  6                  int worksets_begin, 
  7                  int worksets_length, 
  8                  int neighbors_length, 
  9                  global int * neighbors_index, 
 10                   global int * neighbors ,
 11                  int npts_length, 
 12                  global int * npts ,
 13                  int color_length, 
 14                  global int * color ,
 15                  int newcolor_length, 
 16                  global int * newcolor,
 17                  int sizes_length, 
 18                  global int * sizes_index, 
 19                  global int * sizes                 
 20 )
 21 {
 22     int idx = get_global_id(0);
 23     if (idx >= worksets_length)
 24         return;
 25 
 26     // Set sizes to zero, resolveConflicts will reset
 27     // if there's more work to do.
 28     if (idx == 0)
 29         *sizes = 0;
 30 
 31     // Nothing to do if already colored.
 32     if (color[idx] >= 0)
 33         return;
 34 
 35     int nidx = neighbors_index[idx];
 36     int nlast = neighbors_index[idx+1];
 37     int c = -1, offset = 0;
 38     // Loop until colored.
 39     while(c < 0)
 40     {
 41         // Bit flag to store seen neighbor colors.
 42         ulong forbidden = 0;
 43         for(int i = nidx; i < nlast; i++)
 44         {
 45             // Flag any neighbor colors present in the current bitrange.
 46             int n = neighbors[i];
 47             int nc = color[n] - offset;
 48             if (nc >= 0 && nc < FORBIDBITS)
 49                 forbidden |= (1ul << nc);
 50         }
 51         // Check if there's an open color in the current bitrange.
 52         if (forbidden ^ MAXFORBID)
 53         {
 54             ulong x = forbidden;
 55             c = offset;
 56             // Find position of first zero bit.
 57             x = (~x) & (x + 1);
 58             // Color is log2(x)
 59             while(x > 1)
 60             {
 61                 x /= 2;
 62                 c++;
 63             }
 64         }
 65         else
 66         {
 67             // Otherwise we need to try again with the next range of colors.
 68             offset += FORBIDBITS;
 69         }
 70     }
 71     // Record speculative coloring.
 72     newcolor[idx] = c;
 73 }
 74 
 75 kernel void resolveconflicts( 
 76                  int worksets_begin, 
 77                  int worksets_length, 
 78                  int neighbors_length, 
 79                  global int * neighbors_index, 
 80                   global int * neighbors ,
 81                  int npts_length, 
 82                  global int * npts ,
 83                  int color_length, 
 84                  global int * color ,
 85                  int newcolor_length, 
 86                  global int * newcolor,
 87                  int sizes_length, 
 88                  global int * sizes_index, 
 89                   global int * sizes 
 90 )
 91 {
 92     int idx = get_global_id(0);
 93     if (idx >= worksets_length)
 94         return;
 95     // Nothing to do if already colored.
 96     if (color[idx] >= 0)
 97         return;
 98 
 99     int nidx = neighbors_index[idx];
100     int nlast = neighbors_index[idx+1];
101     // Load speculative color.
102     int c = newcolor[idx];
103     int conflict = 0;
104     int npt = npts[idx];
105     for(int i = nidx; i < nlast; i++)
106     {
107         int n = neighbors[i];
108         // Load neighbor's speculative color, which is also
109         // its final color if already accepted.
110         int nc = newcolor[n];
111 
112         // Check for conflict.
113         if (nc == c)
114         {
115             int nnpt = npts[n];
116             // Resolution gives preference to primitives with more points, 
117             // otherwise the one that comes first.
118             // (NOTE: We color in fewer iterations if we prioritize by number
119             // of graph neighbors, but then assuming we process prims by color,
120             // we're usually farther away from original point order leading to many
121             // cache misses and slower downstream processing.)
122             if (nnpt > npt || 
123                 (nnpt == npt && n < idx))
124             {
125                 conflict = 1;
126                 break;
127             }
128         }
129     }
130     
131     // If there's a conflict then reset sizes for more work,
132     // otherewise accept speculative color.
133     if (conflict)
134        *sizes = worksets_length;
135     else
136         color[idx] = c;
137 }

View Code

（7）sort_prims_by_color

根据颜色为primnum排序，为了下面的分workset， 做准备  （因此注意，vellum中Contraint primnum有可能会是要重新排序过的）

（8）create_workset_attrs

 这步比较简单，根据生成两个array数组, @__size ,@__offset。 @__size记录每个color数值的primitive数量，每个color一个workset,@__offset记录每个workset的起始位置。

int @__offsets[];
int @__sizes[];
int offset = 0;
//int @coloridx[];
string colorname = chs("colorname");
int ncolors = nuniqueval(0, "primitive", colorname);
resize(@__offsets, ncolors);
resize(@__sizes, ncolors);
for(int i=0; i < ncolors; i++)
{
    int c = uniqueval(0, "primitive", colorname, i);
    int n = findattribvalcount(0, "primitive", colorname, c);
    @__offsets[i] = offset;
    @__sizes[i] = n;
//    append(@coloridx, expandprimgroup(0, sprintf("\@color=%d", c)));
    offset += n;
}

View Code

（9）rename_workset_attrs

重新命名@__size , @__offset属性 。名字可以在Graph Color上设置，如下图：

@__size  --------->   @workset_lengths

@__offset----------> @workset_begins

 上面是Graph Color 的算法，比较意外的是里面利用二进制的运算，来加大运算的效率。码字不易，转载请标明出处。