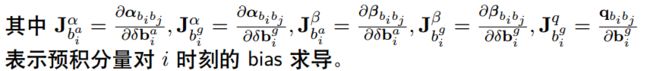VINS-Mono 代码详细解读——IMU预积分的残差、Jacobian和协方差 processIMU()+intergrationBase类+imu_factor.h
前言:
对第k帧和第k+1帧之间所有的IMU进行积分,可得到第K+1帧的PVQ(位置、速度、旋转),作为视觉估计的初始值。
每次qwbt优化更新后,都要重新进行积分,运算量较大。将积分模型转为预积分模型:![]()
PVQ积分公式中的积分项变为相对于第i时刻的姿态,而不是相对于世界坐标系的姿态。
目录
一、IMU离散中值预积分理论基础
1、没预积分:PVQ连续、离散积分
1、IMU模型
2、连续时间IMU运动模型,积分 PVQ(两帧之间)
3、PVQ的中值离散积分(前后IMU)
2、预积分:PVQ连续、离散积分、预积分误差、bias 预积分量
1、 PVQ连续积分(预积分)
2、预积分量
3、 预积分中值离散形式
4、预积分误差
5、bias 预积分量(bias发生变化)
二、预积分的Jacobian和协方差
1、预积分的误差以及线性传递方程
1.预积分误差
2.相邻时刻误差的线性传递方程
3.预积分协方差矩阵
2、预积分的Jacobian和协方差
1、预积分的Jacobian(rv、rq)
2、预积分的协方差
三、processIMU函数
IMU 预积分IntegrationBase类
1、构造函数
2、push_back()函数
3、evaluate()函数
4、propagate()函数
5、中值积分midPointIntegration()
6、repropagate()新的bias重新计算预积分
7、imu_factor.h
一、IMU离散中值预积分理论基础
1、没预积分:PVQ连续、离散积分
1、IMU模型
测量值:加速度计![]() 、陀螺仪
、陀螺仪![]() , 加上了bias游走
, 加上了bias游走![]() 和随机白噪声
和随机白噪声![]() 。
。
真实值:加速度计a、陀螺仪w。
实际情况下,可以获得测量值a^和w^,需要反推真实值。一般忽略随机游走高斯噪声n
w=![]() -bg; a=qwb(
-bg; a=qwb(![]() -ba)-gw;
-ba)-gw;
2、连续时间IMU运动模型,积分 PVQ(两帧之间)
将第k帧和第k+1帧所有的IMU进行积分,可得到第k+1帧的 PVQ,作为视觉估计的初始值。
![]() 和
和![]() 是IMU测量的加速度和角速度,相对于Body坐标系。
是IMU测量的加速度和角速度,相对于Body坐标系。
world坐标系是IMU所在的惯导系。Body系和惯导系关系为:
3、PVQ的中值离散积分(前后IMU)
从第 i个IMU时刻到第 i+1个IMU时刻的积分过程。两个相邻时刻k到k+1的位姿是由第k时刻测量值a^,w^计算得出的。
这与Estimator::processIMU()函数中Ps[j]、Rs[j]、Vs[j]是一致的,代码中j就是此处的i+1
IMU积分出来第 j 时刻数值作为第 j 帧图像初始值。
欧拉法
中值法
2、预积分:PVQ连续、离散积分、预积分误差、bias 预积分量
1、 PVQ连续积分(预积分)
每次qwbt优化更新后,都要重新进行积分,运算量较大。
PVQ积分公式中的积分项变为相对于第i时刻的姿态,而不是相对于世界坐标系的姿态
2、预积分量
IMU预积分量只与IMU测量值有关。(加速度计![]() 、陀螺仪
、陀螺仪![]() )
)
3、 预积分中值离散形式
中值法:k到k+1时刻位姿由两时刻的测量值a w的平均值来计算。
4、预积分误差
一段时间内IMU构建的预积分量作为测量值,与估计值进行相减。
5、bias 预积分量(bias发生变化)
因为 i 时刻的 bias 相关的预积分计算是通过迭代一步一步累计递推的,可以算但是太复杂。所以对于预积分量直接在 i 时刻的 bias 附近用一阶泰勒展开来近似,而不用真的去迭代计算。
二、预积分的Jacobian和协方差
1、预积分的误差以及线性传递方程
预积分模型减小了计算量,但是丢失了一些东西。比如当我们用1个结果代替100个数据点时,转化之前100个点每一个点的不确定度是知道的(IMU数据作为测量值的噪声方差能够标定),但是转化后的1个结果不确定度不知。100个数据积分形成的预积分量方差是多少?这就需要我们在得到IMU预积分后,推导预积分量的协方差,需要直到IMU噪声和预积分量之间的线性递推关系。
IMU在每一个时刻积分出来的值是有误差的,下面对误差进行分析。
1.预积分误差
一段时间内IMU构建的预积分量作为测量值,与估计值进行相减。
上面误差中位移,速度,偏置都是直接相减得到。第二项是关于四元数的旋转误差,其中 [·] xyz 表示只取四元数的虚部 (x,y,z) 组成的三维向量。
2.相邻时刻误差的线性传递方程
误差的传递分为两部分:1)当前时刻误差传递给下一时刻;2)当前时刻测量噪声传递给下一时刻。
测量噪声为:
3.预积分协方差矩阵
其中,![]() 是测量噪声的协方差矩阵,方差从i=0时刻开始递推。
是测量噪声的协方差矩阵,方差从i=0时刻开始递推。
F和G是两时刻间的协方差传递矩阵,![]() 表示各时刻的误差。
表示各时刻的误差。
2、预积分的Jacobian和协方差
两帧之间PVQ和bias变化量的残差为:
残差是15维的,状态量是7+9+7+9维的,所以说,每增加一个IMU约束,总的Jacobian矩阵增加了15行,增加了7+9+7+9列!(需要注意的是,四元数是4维的,但是Localdemension是3维的)。
1、预积分的Jacobian(rv、rq)
优化变量主要包括第i、j时刻的p、q、v、ba、bg:
残差对状态量的Jacobian是什么,对应位置补充上这个J的矩阵块就行了,其他位置还是0。
VINS源码中,在imu_factor.h中的class IMUFactor : public ceres::SizedCostFunction<15, 7, 9, 7, 9> 的函数virtual bool Evaluate()中实现,其中parameters[0~3]分别对应了以上4组优化变量的参数块。对于 Evaluate 输入 double const *const *parameters, parameters[0], parameters[1], parameters[2],parameters[3]分别对应 4 个输入参数, 它们的长度依次是 7,9,7,9,
方式1:整个残差对某个变量求导;
例如:
指的是
主要的四部分(参考崔华坤笔记)为:
方式2:推导关于第i、j帧PVQ的Jacobian(以rv和rq为例)
下面为详细推导,如果不感兴趣,可以直接记住上面方式1的四部分即可。
- rv
由于 rp 和 rv 的误差形式很相近,对各状态量求导的 Jacobian 形式也很相似,所以这里只对 rv 的推导进行详细介绍。
- rq
2、预积分的协方差
![]()
三、processIMU函数
IMU预积分,中值积分得到当前PQV作为优化初值
void Estimator::processIMU(double dt, const Vector3d &linear_acceleration, const Vector3d &angular_velocity)
{
// 1.imu未进来数据
if (!first_imu)
{
first_imu = true;
acc_0 = linear_acceleration;
gyr_0 = angular_velocity;
}
// 2.IMU 预积分类对象还没出现,创建一个
if (!pre_integrations[frame_count])
{
pre_integrations[frame_count] = new IntegrationBase{acc_0, gyr_0, Bas[frame_count], Bgs[frame_count]};
}
if (frame_count != 0)
{ // 3.预积分操作
pre_integrations[frame_count]->push_back(dt, linear_acceleration, angular_velocity);
//if(solver_flag != NON_LINEAR)
tmp_pre_integration->push_back(dt, linear_acceleration, angular_velocity);
// 4.dt、加速度、角速度加到buf中
dt_buf[frame_count].push_back(dt);
linear_acceleration_buf[frame_count].push_back(linear_acceleration);
angular_velocity_buf[frame_count].push_back(angular_velocity);
int j = frame_count;
// 5.采用的是中值积分的传播方式
Vector3d un_acc_0 = Rs[j] * (acc_0 - Bas[j]) - g;// a0=Q(a^-ba)-g 已知上一帧imu速度
Vector3d un_gyr = 0.5 * (gyr_0 + angular_velocity) - Bgs[j];// w=0.5(w0+w1)-bg
Rs[j] *= Utility::deltaQ(un_gyr * dt).toRotationMatrix();
Vector3d un_acc_1 = Rs[j] * (linear_acceleration - Bas[j]) - g;// a1 当前帧imu速度
Vector3d un_acc = 0.5 * (un_acc_0 + un_acc_1);// 中值积分下的加速度a=1/2(a0+a1)
Ps[j] += dt * Vs[j] + 0.5 * dt * dt * un_acc;// P=P+v*t+1/2*a*t^2
Vs[j] += dt * un_acc;// V=V+a*t
}
// 6.更新上一帧的加速度和角速度
acc_0 = linear_acceleration;
gyr_0 = angular_velocity;
}
IMU 预积分IntegrationBase类
1、构造函数
预积分类:加速度计、陀螺仪、线性加速度计ba、陀螺仪bg、雅克比矩阵初始化、协方差矩阵15*15、dt、PVQ
// 预积分类:加速度计、陀螺仪、线性加速度计ba、陀螺仪bg、雅克比矩阵初始化、协方差矩阵15*15、dt、PVQ
IntegrationBase(const Eigen::Vector3d &_acc_0, const Eigen::Vector3d &_gyr_0,
const Eigen::Vector3d &_linearized_ba, const Eigen::Vector3d &_linearized_bg)
: acc_0{_acc_0}, gyr_0{_gyr_0}, linearized_acc{_acc_0}, linearized_gyr{_gyr_0},
linearized_ba{_linearized_ba}, linearized_bg{_linearized_bg},
jacobian{Eigen::Matrix::Identity()}, covariance{Eigen::Matrix::Zero()},
sum_dt{0.0}, delta_p{Eigen::Vector3d::Zero()}, delta_q{Eigen::Quaterniond::Identity()}, delta_v{Eigen::Vector3d::Zero()}
{
noise = Eigen::Matrix::Zero();
noise.block<3, 3>(0, 0) = (ACC_N * ACC_N) * Eigen::Matrix3d::Identity();
noise.block<3, 3>(3, 3) = (GYR_N * GYR_N) * Eigen::Matrix3d::Identity();
noise.block<3, 3>(6, 6) = (ACC_N * ACC_N) * Eigen::Matrix3d::Identity();
noise.block<3, 3>(9, 9) = (GYR_N * GYR_N) * Eigen::Matrix3d::Identity();
noise.block<3, 3>(12, 12) = (ACC_W * ACC_W) * Eigen::Matrix3d::Identity();
noise.block<3, 3>(15, 15) = (GYR_W * GYR_W) * Eigen::Matrix3d::Identity();
} 2、push_back()函数
void push_back(double dt, const Eigen::Vector3d &acc, const Eigen::Vector3d &gyr)
{
dt_buf.push_back(dt);
acc_buf.push_back(acc);
gyr_buf.push_back(gyr);
propagate(dt, acc, gyr);
}3、evaluate()函数
构建残差
// 构建残差residuals
Eigen::Matrix evaluate(const Eigen::Vector3d &Pi, const Eigen::Quaterniond &Qi, const Eigen::Vector3d &Vi, const Eigen::Vector3d &Bai, const Eigen::Vector3d &Bgi,
const Eigen::Vector3d &Pj, const Eigen::Quaterniond &Qj, const Eigen::Vector3d &Vj, const Eigen::Vector3d &Baj, const Eigen::Vector3d &Bgj)
{
Eigen::Matrix residuals;// 残差
Eigen::Matrix3d dp_dba = jacobian.block<3, 3>(O_P, O_BA);
Eigen::Matrix3d dp_dbg = jacobian.block<3, 3>(O_P, O_BG);
Eigen::Matrix3d dq_dbg = jacobian.block<3, 3>(O_R, O_BG);
Eigen::Matrix3d dv_dba = jacobian.block<3, 3>(O_V, O_BA);
Eigen::Matrix3d dv_dbg = jacobian.block<3, 3>(O_V, O_BG);
Eigen::Vector3d dba = Bai - linearized_ba;
Eigen::Vector3d dbg = Bgi - linearized_bg;
Eigen::Quaterniond corrected_delta_q = delta_q * Utility::deltaQ(dq_dbg * dbg);
Eigen::Vector3d corrected_delta_v = delta_v + dv_dba * dba + dv_dbg * dbg;
Eigen::Vector3d corrected_delta_p = delta_p + dp_dba * dba + dp_dbg * dbg;
residuals.block<3, 1>(O_P, 0) = Qi.inverse() * (0.5 * G * sum_dt * sum_dt + Pj - Pi - Vi * sum_dt) - corrected_delta_p;
residuals.block<3, 1>(O_R, 0) = 2 * (corrected_delta_q.inverse() * (Qi.inverse() * Qj)).vec();
residuals.block<3, 1>(O_V, 0) = Qi.inverse() * (G * sum_dt + Vj - Vi) - corrected_delta_v;
residuals.block<3, 1>(O_BA, 0) = Baj - Bai;
residuals.block<3, 1>(O_BG, 0) = Bgj - Bgi;
return residuals;
}
4、propagate()函数
IMU预积分传播方程
积分计算两个关键帧之间IMU测量的变化量:
旋转delta_q 速度delta_v 位移delta_p
加速度的biaslinearized_ba 陀螺仪的Bias linearized_bg
同时维护更新预积分的Jacobian和Covariance,计算优化时必要的参数
预积分传播方程,在预积分传播方程propagate中使用中点积分方法midPointIntegration计算预积分的测量值,中点积分法中主要包含两个部分,分别是得到状态变化量result_delta_q,result_delta_p,result_delta_v,result_linearized_ba,result_linearized_bg和得到跟新协方差矩阵和Jacobian矩阵(注意,虽然得到了雅各比矩阵和协方差矩阵,但是还没有求残差和修正偏置一阶项的状态变量),由于使用的是中点积分,所以需要上一个时刻的IMU数据,包括测量值加速度和角速度以及状态变化量,初始值由构造函数提供。需要注意的是这里定义的delta_p等是累积的变化量,也就是说是从i时刻到当前时刻的变化量,这个才是最终要求的结果(为修正偏置一阶项),而result_delta_q等只是一个暂时的变量,最后残差和雅可比矩阵、协方差矩阵保存在pre_integrations中,还有一个函数这里暂时还没有用到,是在优化的时候才被调用的,但是其属于预积分的内容,evaluate函数在这个函数里面进行了状态变化量的偏置一阶修正以及残差的计算。
步骤2预积分公式(3)未考虑误差,提供imu计算的当前旋转,位置,速度,作为优化的初值
求状态向量对bias的Jacobian,当bias变化较小时,使用Jacobian去更新状态;否则需要以当前imu为参考系,重新预积分,对应repropagation()。同时,需要计算error state model中误差传播方程的系数矩阵F和V:
void propagate(double _dt, const Eigen::Vector3d &_acc_1, const Eigen::Vector3d &_gyr_1)
{
dt = _dt;
acc_1 = _acc_1;
gyr_1 = _gyr_1;
Vector3d result_delta_p;
Quaterniond result_delta_q;
Vector3d result_delta_v;
Vector3d result_linearized_ba;
Vector3d result_linearized_bg;
midPointIntegration(_dt, acc_0, gyr_0, _acc_1, _gyr_1, delta_p, delta_q, delta_v,
linearized_ba, linearized_bg,
result_delta_p, result_delta_q, result_delta_v,
result_linearized_ba, result_linearized_bg, 1);
//checkJacobian(_dt, acc_0, gyr_0, acc_1, gyr_1, delta_p, delta_q, delta_v,
// linearized_ba, linearized_bg);
delta_p = result_delta_p;
delta_q = result_delta_q;
delta_v = result_delta_v;
linearized_ba = result_linearized_ba;
linearized_bg = result_linearized_bg;
delta_q.normalize();
sum_dt += dt;
acc_0 = acc_1;
gyr_0 = gyr_1;
}最主要的还是在midPointIntegration()函数中。
5、中值积分midPointIntegration()
IMU预积分中采用中值积分递推Jacobian和Covariance
构造误差的线性化递推方程,得到Jacobian和Covariance递推公式-> Paper 式9、10、11
void midPointIntegration(double _dt,
const Eigen::Vector3d &_acc_0, const Eigen::Vector3d &_gyr_0,
const Eigen::Vector3d &_acc_1, const Eigen::Vector3d &_gyr_1,
const Eigen::Vector3d &delta_p, const Eigen::Quaterniond &delta_q, const Eigen::Vector3d &delta_v,
const Eigen::Vector3d &linearized_ba, const Eigen::Vector3d &linearized_bg,
Eigen::Vector3d &result_delta_p, Eigen::Quaterniond &result_delta_q, Eigen::Vector3d &result_delta_v,
Eigen::Vector3d &result_linearized_ba, Eigen::Vector3d &result_linearized_bg, bool update_jacobian)
{
//ROS_INFO("midpoint integration");
Vector3d un_acc_0 = delta_q * (_acc_0 - linearized_ba);
Vector3d un_gyr = 0.5 * (_gyr_0 + _gyr_1) - linearized_bg;
result_delta_q = delta_q * Quaterniond(1, un_gyr(0) * _dt / 2, un_gyr(1) * _dt / 2, un_gyr(2) * _dt / 2);
Vector3d un_acc_1 = result_delta_q * (_acc_1 - linearized_ba);
Vector3d un_acc = 0.5 * (un_acc_0 + un_acc_1);
result_delta_p = delta_p + delta_v * _dt + 0.5 * un_acc * _dt * _dt;
result_delta_v = delta_v + un_acc * _dt;
result_linearized_ba = linearized_ba;
result_linearized_bg = linearized_bg;
if(update_jacobian)
{
Vector3d w_x = 0.5 * (_gyr_0 + _gyr_1) - linearized_bg;
Vector3d a_0_x = _acc_0 - linearized_ba;
Vector3d a_1_x = _acc_1 - linearized_ba;
Matrix3d R_w_x, R_a_0_x, R_a_1_x;
//反对称矩阵
R_w_x<<0, -w_x(2), w_x(1),
w_x(2), 0, -w_x(0),
-w_x(1), w_x(0), 0;
R_a_0_x<<0, -a_0_x(2), a_0_x(1),
a_0_x(2), 0, -a_0_x(0),
-a_0_x(1), a_0_x(0), 0;
R_a_1_x<<0, -a_1_x(2), a_1_x(1),
a_1_x(2), 0, -a_1_x(0),
-a_1_x(1), a_1_x(0), 0;
// 对F赋值
MatrixXd F = MatrixXd::Zero(15, 15);
F.block<3, 3>(0, 0) = Matrix3d::Identity();
F.block<3, 3>(0, 3) = -0.25 * delta_q.toRotationMatrix() * R_a_0_x * _dt * _dt +
-0.25 * result_delta_q.toRotationMatrix() * R_a_1_x * (Matrix3d::Identity() - R_w_x * _dt) * _dt * _dt;
F.block<3, 3>(0, 6) = MatrixXd::Identity(3,3) * _dt;
F.block<3, 3>(0, 9) = -0.25 * (delta_q.toRotationMatrix() + result_delta_q.toRotationMatrix()) * _dt * _dt;
F.block<3, 3>(0, 12) = -0.25 * result_delta_q.toRotationMatrix() * R_a_1_x * _dt * _dt * -_dt;
F.block<3, 3>(3, 3) = Matrix3d::Identity() - R_w_x * _dt;
F.block<3, 3>(3, 12) = -1.0 * MatrixXd::Identity(3,3) * _dt;
F.block<3, 3>(6, 3) = -0.5 * delta_q.toRotationMatrix() * R_a_0_x * _dt +
-0.5 * result_delta_q.toRotationMatrix() * R_a_1_x * (Matrix3d::Identity() - R_w_x * _dt) * _dt;
F.block<3, 3>(6, 6) = Matrix3d::Identity();
F.block<3, 3>(6, 9) = -0.5 * (delta_q.toRotationMatrix() + result_delta_q.toRotationMatrix()) * _dt;
F.block<3, 3>(6, 12) = -0.5 * result_delta_q.toRotationMatrix() * R_a_1_x * _dt * -_dt;
F.block<3, 3>(9, 9) = Matrix3d::Identity();
F.block<3, 3>(12, 12) = Matrix3d::Identity();
//cout<<"A"<(0, 0) = 0.25 * delta_q.toRotationMatrix() * _dt * _dt;
V.block<3, 3>(0, 3) = 0.25 * -result_delta_q.toRotationMatrix() * R_a_1_x * _dt * _dt * 0.5 * _dt;
V.block<3, 3>(0, 6) = 0.25 * result_delta_q.toRotationMatrix() * _dt * _dt;
V.block<3, 3>(0, 9) = V.block<3, 3>(0, 3);
V.block<3, 3>(3, 3) = 0.5 * MatrixXd::Identity(3,3) * _dt;
V.block<3, 3>(3, 9) = 0.5 * MatrixXd::Identity(3,3) * _dt;
V.block<3, 3>(6, 0) = 0.5 * delta_q.toRotationMatrix() * _dt;
V.block<3, 3>(6, 3) = 0.5 * -result_delta_q.toRotationMatrix() * R_a_1_x * _dt * 0.5 * _dt;
V.block<3, 3>(6, 6) = 0.5 * result_delta_q.toRotationMatrix() * _dt;
V.block<3, 3>(6, 9) = V.block<3, 3>(6, 3);
V.block<3, 3>(9, 12) = MatrixXd::Identity(3,3) * _dt;
V.block<3, 3>(12, 15) = MatrixXd::Identity(3,3) * _dt;
//step_jacobian = F;
//step_V = V;
// Jacobian和协方差矩阵
jacobian = F * jacobian;
covariance = F * covariance * F.transpose() + V * noise * V.transpose();
}
} 这部分对F和V的赋值就是误差的线性传递函数
之后求解Jacobian和协方差分别为:
6、repropagate()新的bias重新计算预积分
void repropagate(const Eigen::Vector3d &_linearized_ba, const Eigen::Vector3d &_linearized_bg)
{
sum_dt = 0.0;
acc_0 = linearized_acc;// 旧的加速度和陀螺仪
gyr_0 = linearized_gyr;
delta_p.setZero();
delta_q.setIdentity();
delta_v.setZero();
linearized_ba = _linearized_ba;// 更新Bias
linearized_bg = _linearized_bg;
jacobian.setIdentity();
covariance.setZero();
for (int i = 0; i < static_cast(dt_buf.size()); i++)
propagate(dt_buf[i], acc_buf[i], gyr_buf[i]);
} 7、imu_factor.h
主函数为
virtual bool Evaluate(double const *const *parameters, double *residuals, double **jacobians) const1、填充优化变量,i和j时刻的4组优化变量参数块
// 1、优化变量:i和j时刻的4组优化变量参数块
Eigen::Vector3d Pi(parameters[0][0], parameters[0][1], parameters[0][2]);
Eigen::Quaterniond Qi(parameters[0][6], parameters[0][3], parameters[0][4], parameters[0][5]);
Eigen::Vector3d Vi(parameters[1][0], parameters[1][1], parameters[1][2]);
Eigen::Vector3d Bai(parameters[1][3], parameters[1][4], parameters[1][5]);
Eigen::Vector3d Bgi(parameters[1][6], parameters[1][7], parameters[1][8]);
Eigen::Vector3d Pj(parameters[2][0], parameters[2][1], parameters[2][2]);
Eigen::Quaterniond Qj(parameters[2][6], parameters[2][3], parameters[2][4], parameters[2][5]);
Eigen::Vector3d Vj(parameters[3][0], parameters[3][1], parameters[3][2]);
Eigen::Vector3d Baj(parameters[3][3], parameters[3][4], parameters[3][5]);
Eigen::Vector3d Bgj(parameters[3][6], parameters[3][7], parameters[3][8]);2、构建IMU残差residual
主要通过调用 pre_integration->evaluate,预积分模块中evaluate函数。也就是上面的3 evaluate()函数
// 2、构建IMU残差residual
Eigen::Map> residual(residuals);// 已知残差
residual = pre_integration->evaluate(Pi, Qi, Vi, Bai, Bgi,
Pj, Qj, Vj, Baj, Bgj);
// LLT分解,residual 还需乘以信息矩阵的sqrt_info
// 因为优化函数其实是d=r^T P^-1 r ,P表示协方差,而ceres只接受最小二乘优化
// 因此需要把P^-1做LLT分解,使d=(L^T r)^T (L^T r) = r'^T r
Eigen::Matrix sqrt_info = Eigen::LLT>(pre_integration->covariance.inverse()).matrixL().transpose();
residual = sqrt_info * residual; 3、获取预积分的误差递推函数中pqv关于ba、bg的Jacobian
// 3、获取预积分的误差递推函数中pqv关于ba、bg的Jacobian
double sum_dt = pre_integration->sum_dt;
Eigen::Matrix3d dp_dba = pre_integration->jacobian.template block<3, 3>(O_P, O_BA);
Eigen::Matrix3d dp_dbg = pre_integration->jacobian.template block<3, 3>(O_P, O_BG);
Eigen::Matrix3d dq_dbg = pre_integration->jacobian.template block<3, 3>(O_R, O_BG);
Eigen::Matrix3d dv_dba = pre_integration->jacobian.template block<3, 3>(O_V, O_BA);
Eigen::Matrix3d dv_dbg = pre_integration->jacobian.template block<3, 3>(O_V, O_BG);
if (pre_integration->jacobian.maxCoeff() > 1e8 || pre_integration->jacobian.minCoeff() < -1e8)
{
ROS_WARN("numerical unstable in preintegration");
//std::cout << pre_integration->jacobian << std::endl;
/// ROS_BREAK();
}接下来便是对4个模块进行求解
4、第i帧的IMU位姿 pbi、qbi
// 4、第i帧的IMU位姿 pbi、qbi
if (jacobians[0])
{
Eigen::Map> jacobian_pose_i(jacobians[0]);
jacobian_pose_i.setZero();
jacobian_pose_i.block<3, 3>(O_P, O_P) = -Qi.inverse().toRotationMatrix();
jacobian_pose_i.block<3, 3>(O_P, O_R) = Utility::skewSymmetric(Qi.inverse() * (0.5 * G * sum_dt * sum_dt + Pj - Pi - Vi * sum_dt));
#if 0
jacobian_pose_i.block<3, 3>(O_R, O_R) = -(Qj.inverse() * Qi).toRotationMatrix();
#else
Eigen::Quaterniond corrected_delta_q = pre_integration->delta_q * Utility::deltaQ(dq_dbg * (Bgi - pre_integration->linearized_bg));
jacobian_pose_i.block<3, 3>(O_R, O_R) = -(Utility::Qleft(Qj.inverse() * Qi) * Utility::Qright(corrected_delta_q)).bottomRightCorner<3, 3>();
#endif
jacobian_pose_i.block<3, 3>(O_V, O_R) = Utility::skewSymmetric(Qi.inverse() * (G * sum_dt + Vj - Vi));
jacobian_pose_i = sqrt_info * jacobian_pose_i;
if (jacobian_pose_i.maxCoeff() > 1e8 || jacobian_pose_i.minCoeff() < -1e8)
{
ROS_WARN("numerical unstable in preintegration");
//std::cout << sqrt_info << std::endl;
//ROS_BREAK();
}
} 5、第i帧的imu速度vbi、bai、bgi
// 6、第i帧的imu速度vbi、bai、bgi
if (jacobians[1])
{
Eigen::Map> jacobian_speedbias_i(jacobians[1]);
jacobian_speedbias_i.setZero();
jacobian_speedbias_i.block<3, 3>(O_P, O_V - O_V) = -Qi.inverse().toRotationMatrix() * sum_dt;
jacobian_speedbias_i.block<3, 3>(O_P, O_BA - O_V) = -dp_dba;
jacobian_speedbias_i.block<3, 3>(O_P, O_BG - O_V) = -dp_dbg;
#if 0
jacobian_speedbias_i.block<3, 3>(O_R, O_BG - O_V) = -dq_dbg;
#else
//Eigen::Quaterniond corrected_delta_q = pre_integration->delta_q * Utility::deltaQ(dq_dbg * (Bgi - pre_integration->linearized_bg));
//jacobian_speedbias_i.block<3, 3>(O_R, O_BG - O_V) = -Utility::Qleft(Qj.inverse() * Qi * corrected_delta_q).bottomRightCorner<3, 3>() * dq_dbg;
jacobian_speedbias_i.block<3, 3>(O_R, O_BG - O_V) = -Utility::Qleft(Qj.inverse() * Qi * pre_integration->delta_q).bottomRightCorner<3, 3>() * dq_dbg;
#endif
jacobian_speedbias_i.block<3, 3>(O_V, O_V - O_V) = -Qi.inverse().toRotationMatrix();
jacobian_speedbias_i.block<3, 3>(O_V, O_BA - O_V) = -dv_dba;
jacobian_speedbias_i.block<3, 3>(O_V, O_BG - O_V) = -dv_dbg;
jacobian_speedbias_i.block<3, 3>(O_BA, O_BA - O_V) = -Eigen::Matrix3d::Identity();
jacobian_speedbias_i.block<3, 3>(O_BG, O_BG - O_V) = -Eigen::Matrix3d::Identity();
jacobian_speedbias_i = sqrt_info * jacobian_speedbias_i;
//ROS_ASSERT(fabs(jacobian_speedbias_i.maxCoeff()) < 1e8);
//ROS_ASSERT(fabs(jacobian_speedbias_i.minCoeff()) < 1e8);
} 6、第j帧的IMU位姿 pbj、qbj
// 7、第j帧的IMU位姿 pbj、qbj
if (jacobians[2])
{
Eigen::Map> jacobian_pose_j(jacobians[2]);
jacobian_pose_j.setZero();
jacobian_pose_j.block<3, 3>(O_P, O_P) = Qi.inverse().toRotationMatrix();
#if 0
jacobian_pose_j.block<3, 3>(O_R, O_R) = Eigen::Matrix3d::Identity();
#else
Eigen::Quaterniond corrected_delta_q = pre_integration->delta_q * Utility::deltaQ(dq_dbg * (Bgi - pre_integration->linearized_bg));
jacobian_pose_j.block<3, 3>(O_R, O_R) = Utility::Qleft(corrected_delta_q.inverse() * Qi.inverse() * Qj).bottomRightCorner<3, 3>();
#endif
jacobian_pose_j = sqrt_info * jacobian_pose_j;
//ROS_ASSERT(fabs(jacobian_pose_j.maxCoeff()) < 1e8);
//ROS_ASSERT(fabs(jacobian_pose_j.minCoeff()) < 1e8);
} 7、第j帧的IMU速度vbj、baj、bgj
// 8、第j帧的IMU速度vbj、baj、bgj
if (jacobians[3])
{
Eigen::Map> jacobian_speedbias_j(jacobians[3]);
jacobian_speedbias_j.setZero();
jacobian_speedbias_j.block<3, 3>(O_V, O_V - O_V) = Qi.inverse().toRotationMatrix();
jacobian_speedbias_j.block<3, 3>(O_BA, O_BA - O_V) = Eigen::Matrix3d::Identity();
jacobian_speedbias_j.block<3, 3>(O_BG, O_BG - O_V) = Eigen::Matrix3d::Identity();
jacobian_speedbias_j = sqrt_info * jacobian_speedbias_j;
//ROS_ASSERT(fabs(jacobian_speedbias_j.maxCoeff()) < 1e8);
//ROS_ASSERT(fabs(jacobian_speedbias_j.minCoeff()) < 1e8);
}