Structural Consistency and Controllability for Diverse Colorization_ECCV_2018
论文下载:Structural Consistency and Controllability for Diverse Colorization_ECCV_2018
摘要
对给定的灰度图像进行着色是媒体和广告业的一项重要任务。由于颜色化固有的模糊性(许多着色通常是合理的),最近的方法开始显式地建模多样性。然而,现有方法独立对于每一个像素预测色度,很少考虑结构不一致这一最明显的缺陷。为了解决这个问题,论文开发了一个基于条件随机场的变分自动编码器公式,它能够在考虑结构一致性的同时实现多样性。此外,论文引入了一种可控性机制,它可以包含来自不同来源的外部约束,包括用户界面。与现有基线方法相比,论文的方法在LFW、LSUN Church和ILSVRC-2015数据集上获得了更加多样化和全局一致的着色。
引言
图像的彩色化需要预测所提供的灰度输入的两个缺失通道。与其他计算机视觉任务(如单目深度预测或语义分割)类似,颜色化是不适定的。然而,与上述任务不同的是,颜色化也是模棱两可的,也就是说,许多不同的着色都是完全合理的。例如,不同颜色的衬衫或汽车是非常合理的,而正面色调的多样性肯定较少。捕捉这些微妙之处是一个非常重要的问题。
因此,早期的着色工作是交互式的,需要一些参考彩色图像或涂鸦。为了使这一过程自动化,经典的方法将任务描述为一个预测问题,使用有限大小的数据集。最近的深度学习方法被证明可以在更大的数据集中捕捉更复杂的颜色属性。然而,所有这些方法都有一个共同点,就是对给定的灰度图像只进行一次着色。因此,模糊性和多模态往往没有得到充分的建模。为此,甚至最近,使用生成建模技术(如变分自动编码器、生成对抗网或自回归模型等)描述了用于着色的不同输出空间分布。
虽然基于生成技术的方法可以通过捕捉数据集分布来生成不同的颜色,但它们通常缺乏结构一致性,例如衬衫的某些部分颜色不同或汽车有斑点。不一致是由于这样一个事实,即结构连贯性只在使用基于深网的生成方法时才被隐含地鼓励。此外,现有的各种着色技术也常常缺乏一种可控性,允许在保持结构一致性的同时进行干扰。
为了解决一致性和可控性,论文提出的方法用高斯-马尔可夫随机公式来增强变分自动编码器的输出空间。论文以一种端到端的方式进行训练,能够显式地建模图像中多个像素之间的结构关系。除了学习像素之间的结构一致性之外,论文还开发了一个包含外部约束的控制机制。这使得用户可以使用彩色标记与生成过程进行交互。论文在野外(LFW)、LSUN Church和ILSVRC-2015数据集上展示了视觉上吸引人的结果,并通过用户研究评估了照片真实性方面。
高斯条件马尔可夫随机场
马尔可夫随机场和它们的条件计数器部分是一个令人信服的工具,可以从理论上对变量之间的相关性进行建模,因此它们非常适合于我们感兴趣的着色任务,因为我们对不同像素之间的颜色依赖性很感兴趣。然而,在大输出空间上经典马尔可夫随机场中最有可能构形的推断在计算上要求很高,并且只有在少数特殊情况下才可处理。
高斯-马尔可夫随机场代表了其中一种允许有效和精确推断的情况。它们将数据的联合分布(例如,图像的双色通道的像素值)建模为多变量高斯密度。高斯-马尔可夫随机场过去被用于不同的计算机视觉应用,包括语义分割、人体部分分割和显著性估计、图像标记和图像去噪。论文使用完全连通的高斯条件随机数,并用一个深度网络进行端到端的参数学习。除了结构上的一致性,论文的目标是联合建模模糊性,这是着色任务的固有部分。为此,论文使用可变的自动编码器。
可变自动编码器
变分自动编码器(VAEs)和条件变量(conditional VAEs,CVAEs)被用来模拟各种任务中的模糊性。它们基于流形假设,即高维数据点(如彩色图像)可以基于低维嵌入和一些辅助数据(如灰度图像)进行建模。形式上,假设了低维嵌入空间的存在性和通过条件p_θ (x|z,g)的变换。给定一个包含一对条件信息g和期望输出x的数据集D,即,给定D={(g,x)},CVAEs通过考虑以下恒等式,得出条件对数似然ln〖p_θ (x|g)〗的最大化:
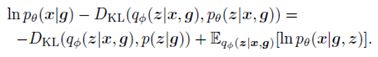 (1)
(1)
这里,D_KL (∙,∙)表示两个分布之间的Kullback-Leibler(KL)散度,并用q_∅ (z|x,g)来近似模拟条件p_θ (x|g,z)的深度网络的难处理后验p_θ (z|x,g)。后验函数的近似值,即q_∅ (z|x,g)被称为编码器,而用于重构的深度网络,即用于建模条件p_θ (x|g,z),通常称为解码器。
由于KL散度是非负的,当考虑上式中给出的恒等式的右侧时,得到了数据对数似然ln〖p_θ (x|g)〗的一个下界。CVAEs最小化这个下界的否定版本,即
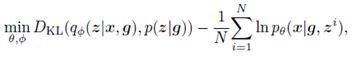 (2)
(2)
其中期望等式E_(q_ϕ (z|x,g))通过N个样本z^i~q_ϕ (z|x,g)近似。为了简单起见,论文忽略了数据集D中样本的求和,并提供了训练单个对(x,g)的目标。
方法概述
论文提出的彩色化模型具有以下几个吸引人的特性:(1)多样性,即它为单个灰度图像生成多样化和逼真的着色;(2)全局一致性,通过使用全连通高斯条件随机场(G-CRF)显式地建模生成的颜色字段的输出空间分布来实现;(3)可控性,即模型可以在运行时有效地考虑外部约束。例如,用户可以强制给定的对象具有特定的颜色,或者强制两个分离的区域具有相同的着色效果。

图1. 一种基于全连通高斯条件随机场(G-CRF)的可变全局相干着色VAE。为了产生不同的颜色,我们使用混合密度网络(MDN)来表示给定灰度图像g的彩色图像嵌入z的多模分布。在测试时,我们对随后解码的多个嵌入进行采样以生成不同的着色。为了保证全局一致性,我们使用G-CRF对解码器的输出空间分布进行建模。
图1展示了方法的概述。给定一个像素为P的灰度图像g,论文的目标是在Lab颜色空间中生成由两个通道x_a∈RP和x_b∈RP组成的不同颜色场x∈R^2P。此外,我们在全局范围内加强空间相干性,并使用高斯-马尔可夫随机场来模拟输出空间分布,实现可控性。
为了产生多种着色效果,我们需要学习给定灰度图像g的色域x的多模条件分布p(x|g)。但是,学习这个条件是一个挑战,因为颜色场x和强度场g是高维的。因此,用于学习p(x|g)的训练样本稀疏分散,即使使用大型数据集也很难捕捉到分布。因此,我们假设流形假设成立,我们选择学习一个条件p(x|z,g),基于从x和g捕获的低维嵌入z,使用一个可变的自动编码器,通过编码器来近似难处理的后验p(z|x,g)。Deshpande等人。论文选择了一个多阶段的培训程序,直接从p(z|g)中取样。
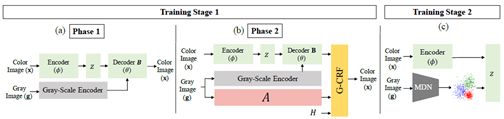
图2. 模型架构和培训过程概述。在第一个训练阶段,论文使用VAE学习以灰度图像g为条件的色域x的低维嵌入z。为了从结构上区分颜色,论文首先在阶段1中学习一元项B,然后在阶段2中学习通过施加约束,即强度相似的像素应具有相似的定植度,对图像的结构进行编码的精度矩阵。为了实现可控制性,论文使用矩阵H中指定的训练计划来逐步掩盖一元项B中的解码像素颜色,因此逐渐依赖A矩阵从一元项中恢复着色。在第二个训练阶段,论文使用MDN来学习给定灰度图像的潜在嵌入的多模式分布。
为了捕获低维嵌入,在第一个训练阶段,给定灰度图像g和彩色图像x,论文使用一个变分自动编码器来学习彩色嵌入z的参数化单峰高斯编码器分布q_ϕ (z│x,g)~N(μ_ϕ,σ_ϕ^2 I)(如图2(a))。同时,我们学习了译码器p_θ (x|z,g)的参数θ。
重要的是,编码器q_θ (z|x,g)在映射到潜在表示z时同时利用了彩色图像x和灰度强度g。由于使用了彩色图像,论文期望可以使用单峰分布(即,论文使用高斯分布)来捕获该映射。
然而,在推理过程中,可以从灰度图像g中获得多种颜色。因此,当只对灰度图像g进行处理时,论文并不期望单峰分布p(z|g)在测试中是准确的。
为了解决这个问题,在第二个训练阶段,论文训练混合密度网络(MDN)p_ψ (z|g),以最大化从q_ϕ (z|x,g)采样的嵌入z的对数可能性(如图2(b))。直观地说,对于灰度图像,MDN可以预测对应于不同颜色化的M高斯分量的参数。在第一阶段学习到的嵌入z随后被绑定到这些组件中的一个。其余部分采用近距离灰度图像嵌入法进行优化。
在测试时,从MDNp_ψ (z|g)中采样N个不同的嵌入〖{z}〗_(k=1)^N,并由解码器转换成不同的着色,如图1所示。为了鼓励全局一致着色并确保可控性,论文使用一个完全连通的G-CRF层来模拟输出空间分布。G-CRF后面的负对数具有二次能量函数的形式:
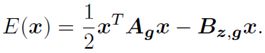 (3)
(3)
它捕捉a和b通道像素颜色之间的一元和高阶相关(HOC)。直观地说,联合G-CRF使模型能够捕获更多的全局图像统计信息,从而产生更多的空间相干着色。一元项B_(z,g)从VAE解码器获得,并对每像素的颜色进行编码。HOC术语A_g=f(A_g^T A_g)负责对输入图像的结构进行编码。它是低阶像素嵌入A_g的内积函数,从灰度图像中学习并测量像素强度之间的成对相似性。直觉是具有相似强度的像素应该有相似的着色。HOC术语在测试时获得的不同着色之间共享。除了全局一致性之外,它还通过正确传播以一元术语编码的用户编辑来实现可控性。由于HOC项的对称性,二次能量函数具有唯一的全局最小值,可通过求解线性方程组获得:
![]() (4)
(4)
随后,为了简单起见,论文去掉了A和B对g和z的依赖关系。
推论
为了确保全局一致的着色,论文利用图像的结构。为此,论文鼓励两个像素在亮度相似的情况下具有相似的颜色。因此,论文希望最小化a和b通道的颜色场x与相似像素处颜色的加权平均值之间的差异。更正式地说,论文想要鼓励等式x_a=S ̂x_a和x_b=S ̂x_b,其中S ̂=softmax(A^T A)是通过对A^T A生成的矩阵的每一行应用softmax函数得到的相似矩阵。为了简化,论文使用块结构矩阵S=diag(S ̂,S ̂)。
除了捕捉结构之外,论文还通过对计算出的一元项B中的用户输入进行编码来获得颜色先验和可控性。因此,论文添加了约束Hx=α,其中H是一个对角线矩阵,其中0和1项对应于像素的值是否由用户指定,以及一个对每个像素的颜色进行编码的向量应设置为α。
根据上述直觉,论文得到了要最小化的二次能量函数:

β是一个超参数。这对应于1/2 x^T Ax+Bx+C形式的二次能量函数,其中A=(S-I)^T (S-I)+βH^T H,B=-2βα^T H和C=βα^T α。很明显,一元术语只编码颜色统计信息,而HOC术语只负责结构的一致性。直观地说,条件p_θ (x|g,z)被解释为高斯多变量密度:
![]() (5)
(5)
由上述能量函数E_(θ,g,z)参数化,可以很容易地证明A是一个正的负全秩矩阵。因此,对于严格正定矩阵,推理可简化为求解线性方程组:
![]() (6)
(6)
论文利用矩阵的LU分解来求解上述线性系统。
学习
图2表示训练的两个阶段,以确保颜色和结构的分离,并产生不同的着色效果。论文还讨论了在每个阶段对公式2中给出的损失的修正。
第1阶段:训练结构化输出空间可变自动编码器:
在第一个训练阶段,论文使用变分自动编码器公式来学习给定颜色的低维嵌入。这一阶段分为两个阶段,以确保颜色和结构的脱节。在第一阶段,论文学习VAE解码器产生的一元项。在第二阶段,论文确定了除了解码器的两个最顶层之外的VAE的权重,并从灰度图像中学习P像素的D维嵌入矩阵A∈R(D×P)。通过对每一行AT A应用softmax得到的矩阵S ̂用于鼓励a和b通道的x=Sx之前的平滑度。为了确保S矩阵学习可控性阶段所需的结构,在可控性阶段,稀疏用户编辑需要传播,论文遵循一个训练计划,其中一元项使用H矩阵逐步屏蔽。利用所学习的结构,从稀疏的一元数据中重建输入图像。当需要从稀疏的用户编辑进行着色时,论文从等式6中为学习的HOC项和编码用户编辑的H矩阵和项求解线性系统,如图2所示。我们在实验部分详细解释了训练时间表。
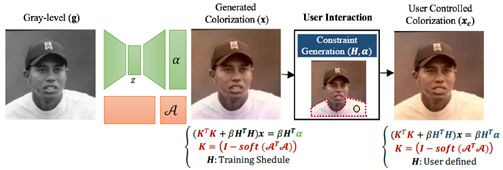
图3. 可控性:给定一幅灰度图像,我们学习如何从着色中分离结构。HOC术语用于传播编码在H和α术语编码的稀疏用户编辑。
考虑到G-CRF后验的新定义,第一个训练阶段的计划如下:
![]()
随后论文使用术语L来表示这个程序的目标函数。
第2阶段:训练混合密度网络(MDN):
因为颜色图像x在测试期间不可用,在第二个训练阶段,论文使用参数分布p_ψ (z|g)捕捉在第一个训练阶段学习到的近似后验q_ϕ (z|x,g)。由于对彩色图像x的依赖性,论文期望近似后验q_ϕ (z|x,g)比p_ψ (z|g)更容易建模。因此,论文让p_ψ (z|g)是一个含有M个分量的高斯混合模型(GMM)。它的均值、方差和分量权重通过一个带参数ψ的混合密度网络(MDN)进行参数化。直观地说,对于给定的灰度图像,论文期望M分量对应于不同的着色。通过最小化负条件对数似然,将从第一个训练阶段学习到的颜色嵌入z映射到其中一个分量,即最小化:
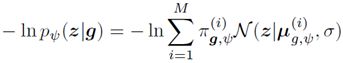
因此,π_(g,ψ)((i)),μ_(g,ψ)((i))和σ分别指由ψ参数化的MDN网络学习的GMM的混合系数、均值和固定协方差。然而,最小化-ln〖p_ψ (z|g)〗是困难的,因为它涉及计算不同指数分量上求和的对数。为了避免这种情况,论文明确地将编码z分配给高斯分量m,其平均值最接近z,即m=argmin┬i‖z-μ_(g,ψ)^((i)) ‖。因此,将负对数似然损失-ln〖p_ψ (z|g)〗简化为求解以下程序:
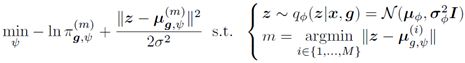
注意,潜在样本z是从第一阶段学习的近似后验q_ϕ (z|x,g)中获得的。





